
题目列表(包括答案和解析)
21.(本小题满分12分)
已知函数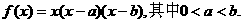
(Ⅰ)设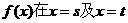 处取到极值,其中
处取到极值,其中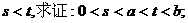
(Ⅱ)设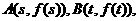 求证:线段AB的中点C在曲线y=f(x)上;
求证:线段AB的中点C在曲线y=f(x)上;
(Ⅲ)若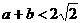 ,求证:过原点且与曲线y=f(x)相切的两条直线不可能垂直.
,求证:过原点且与曲线y=f(x)相切的两条直线不可能垂直.
解:(Ⅰ)以线段AB的中点O为原点,直线AB为x轴建立直角坐标系,
作CD⊥AB于D, 由题知: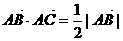 ①
①
而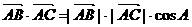 ②
②
由①②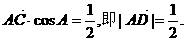 ………………2分
………………2分
同理,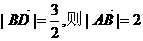 ∴A(-1,0)、B(1,0)……4分
∴A(-1,0)、B(1,0)……4分
设双曲线方程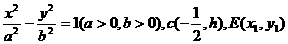
由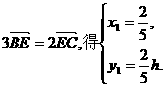 …………6分
…………6分
因为E、C两点在双曲线上,所以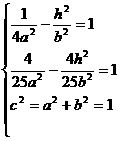 ………………8分
………………8分
解得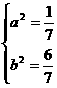 ,∴双曲线方程为
,∴双曲线方程为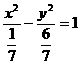 …………10分
…………10分
(Ⅱ)设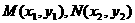
∵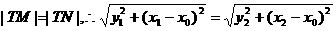
∴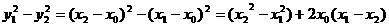 ①
①
又M、N在双曲线上,满足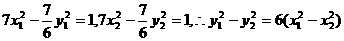 ②
②
将②代入①,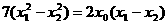
∵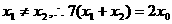 …………………………12分
…………………………12分
又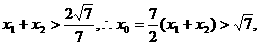
∴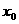 取值范围为(
取值范围为(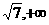 ) ………………14分
) ………………14分
20.(本小题满分12分)
数列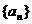 ,设Sn是数列的前n项和,并且满足
,设Sn是数列的前n项和,并且满足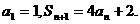
(Ⅰ)令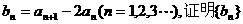 是等比数列,并求{bn}的通项公式;
是等比数列,并求{bn}的通项公式;
(Ⅱ)令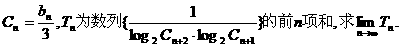
解:(Ⅰ)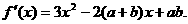
依题意知,s、t是二次方程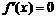 的两个实根.
的两个实根.
∵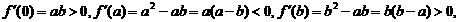 ……2分
……2分
∴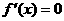 在区间(0,a)与(a,b)内分别有一个实根.
在区间(0,a)与(a,b)内分别有一个实根.
∵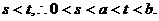 …………4分
…………4分
(Ⅱ)由s、t是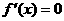 的两个实根,知
的两个实根,知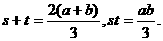
∴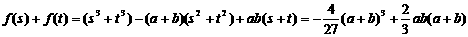 …6分
…6分
∵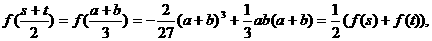
故AB的中点C(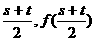 )在曲线y=f(x)上. ……8分
)在曲线y=f(x)上. ……8分
(Ⅲ)过曲线上点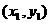 的切线方程为
的切线方程为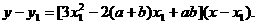
∵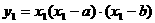 ,又切线过原点.
,又切线过原点.
∴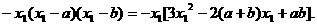
解得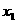 =0,或
=0,或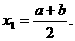
当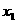 =0时,切线的斜率为ab;当
=0时,切线的斜率为ab;当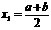 时,切线的斜率为
时,切线的斜率为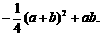 ……10分
……10分
∵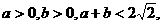 ∴两斜率之积
∴两斜率之积
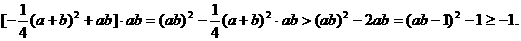
故两切线不垂直. ………………12分
2.大连二模
20. (本题满分14分)
已知直线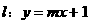 与曲线
与曲线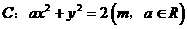 交于两点A、B。
交于两点A、B。
(1)设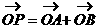 ,当
,当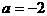 时,求点P的轨迹方程;
时,求点P的轨迹方程;
(2)是否存在常数a,对任意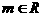 ,都有
,都有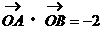 ?如果存在,求出a的值;如果不存在,说明理由。
?如果存在,求出a的值;如果不存在,说明理由。
(3)是否存在常数m,对任意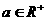 ,都有
,都有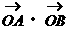 为常数?如果存在,求出m的值;如果不存在,说明理由。
为常数?如果存在,求出m的值;如果不存在,说明理由。
解:(1)设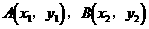 ,则
,则
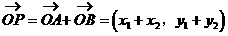
由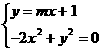 消去y,得:
消去y,得:
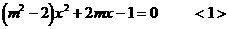
依题意有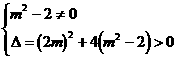 解得:
解得:
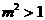 且
且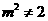 ,即
,即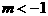 或
或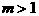 且
且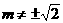
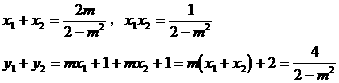
∴点P的坐标为: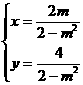 消去m,得:
消去m,得:
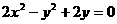 ,即
,即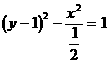
由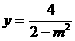 ,得
,得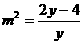
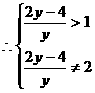 ,解得
,解得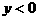 或
或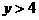
∴点P的轨迹方程为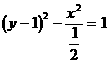 (
(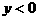 或
或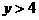 )………………5分
)………………5分
(2)假设存在这样的常数a
由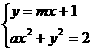 消去y得:
消去y得:
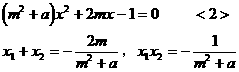
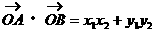
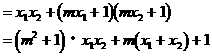
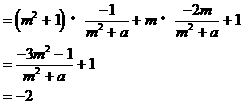
解得: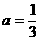
当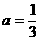 时,
时,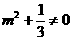 ,且方程<2>判别式
,且方程<2>判别式
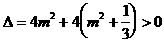
∴对任意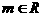 ,A、B两点总存在,故当
,A、B两点总存在,故当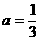 时,对任意
时,对任意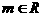 ,都有
,都有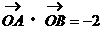 ………………10分
………………10分
(3)假设这样的常数m存在,对任意的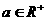 ,使
,使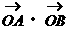 为一常数M。
为一常数M。
即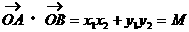
即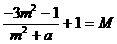
化简,得: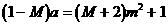
∵a为任意正实数
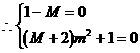 ,即
,即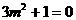 ,矛盾。
,矛盾。
故这样的常数m不存在。………………14分
19. (本题满分14分)
已知点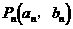 满足:
满足: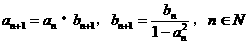 ,且已知
,且已知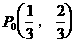
(1)求过点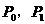 的直线
的直线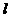 的方程;
的方程;
(2)判断点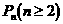 与直线
与直线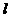 的位置关系,并证明你的结论;
的位置关系,并证明你的结论;
(3)求点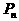 的极限位置。
的极限位置。
解:(1)由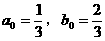 ,得:
,得:
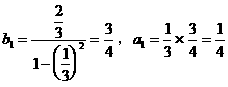
显然直线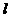 的方程为
的方程为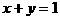 ………………3分
………………3分
(2)由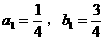 ,得:
,得:
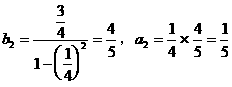
∴点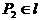 ,猜想点
,猜想点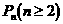 在直线
在直线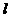 上,以下用数学归纳法证明:
上,以下用数学归纳法证明:
当n=2时,点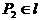
假设当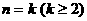 时,点
时,点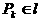 ,即
,即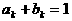
当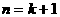 时,
时,
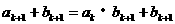
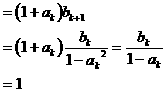
∴点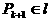
综上,点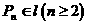 ………………8分
………………8分
(3)由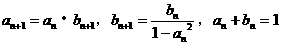 ,得:
,得:
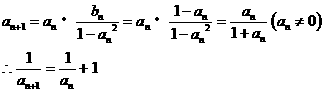
∴数列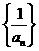 是以
是以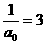 为首项,公差为1的等差数列
为首项,公差为1的等差数列
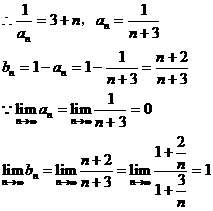
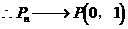
即点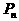 的极限位置为点P(0,1)………………14分
的极限位置为点P(0,1)………………14分
1.北京宣武区二模
22.(本小题满分14分)
已知函数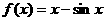
(Ⅰ)若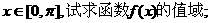
(Ⅱ)若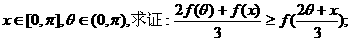
(Ⅲ)若
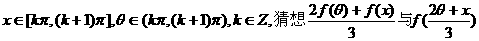 的大小关系(不必写出比较过程).
的大小关系(不必写出比较过程).
解:(Ⅰ)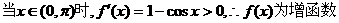
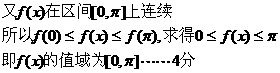
(Ⅱ)设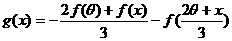
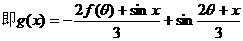
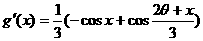 ……6分
……6分
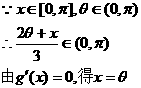
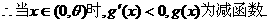
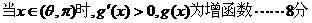

(Ⅲ)在题设条件下,当k为偶数时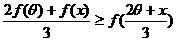
当k为奇数时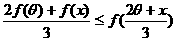 ……14分
……14分
21.(本小题满分12分)
垂直于x轴的直线交双曲线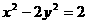 于M、N不同两点,A1、A2分别为双曲线的左顶点和右顶点,设直线A1M与A2N交于点P(x0,y0)
于M、N不同两点,A1、A2分别为双曲线的左顶点和右顶点,设直线A1M与A2N交于点P(x0,y0)
(Ⅰ)证明: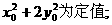
(Ⅱ)过P作斜率为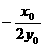 的直线l,原点到直线l的距离为d,求d的最小值.
的直线l,原点到直线l的距离为d,求d的最小值.
解(Ⅰ)证明: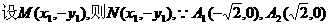
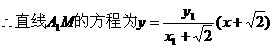 ①
①
直线A2N的方程为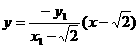 ②……4分
②……4分
①×②,得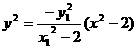
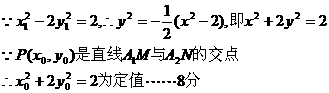
(Ⅱ)
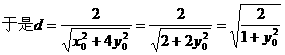 ……10分
……10分
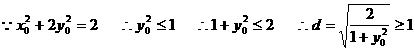
当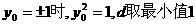 ……12分
……12分
3.唐山二模
22.(本小题满分14分)
(理)给定正整数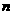 和正数
和正数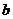 ,对于满足条件
,对于满足条件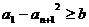 的所有无穷等差数列
的所有无穷等差数列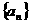 ,试求
,试求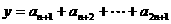 的最大值,并求出
的最大值,并求出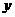 取最大值时
取最大值时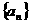 的首项和公差.
的首项和公差.
(文)给定正整数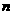 和正数
和正数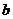 ,对于满足条件
,对于满足条件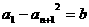 的所有无穷等差数列
的所有无穷等差数列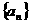 ,试求
,试求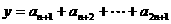 的最大值,并求出
的最大值,并求出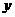 取最大值时
取最大值时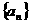 的首项和公差.
的首项和公差.
(理)解:设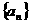 公差为
公差为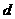 ,则
,则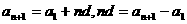 . 3分
. 3分
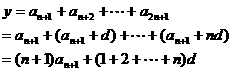
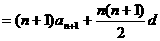 4分
4分
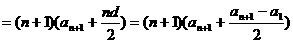
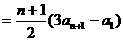 . 7分
. 7分
又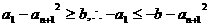 .
.
∴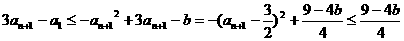 ,
,
当且仅当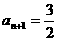 时,等号成立. 11分
时,等号成立. 11分
∴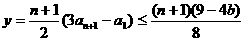 . 13分
. 13分
当数列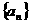 首项
首项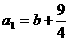 ,公差
,公差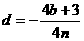 时,
时,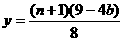 ,
,
∴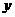 的最大值为
的最大值为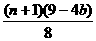 . 14分
. 14分
(文)解:设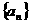 公差为
公差为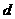 ,则
,则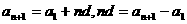 . 3分
. 3分
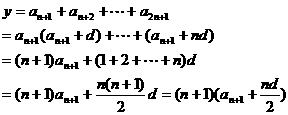
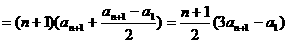 , 6分
, 6分
又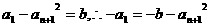 .
.
∴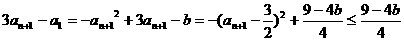 .
.
当且仅当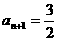 时,等号成立. 11分
时,等号成立. 11分
∴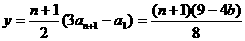 . 13分
. 13分
当数列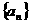 首项
首项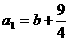 ,公差
,公差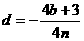 时,
时,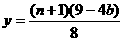 .
.
∴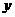 的最大值为
的最大值为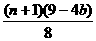 . 14分
. 14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com