
题目列表(包括答案和解析)
8. P为椭圆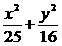 =1上一点,M、N分别是圆(x+3) 2+y2=4和(x-3) 2+y2=1上的点,则|PM|+|PN|的取值范围是( )
=1上一点,M、N分别是圆(x+3) 2+y2=4和(x-3) 2+y2=1上的点,则|PM|+|PN|的取值范围是( )
A. 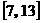 |
B.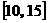 |
C. 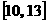 |
D. 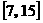 |
第Ⅱ卷 (非选择题 共110分)
7. 已知命题(1)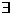
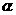
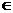
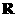 ,使
,使 成立;(2)
成立;(2) 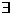
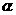
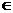
 ,使
,使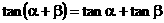 成立;(3)
成立;(3) 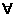
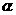
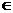
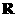 ,都有
,都有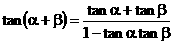 成立.
成立.
其中正确命题的个数是 ( )
|
A. 3 |
B. 2 |
C. 1 |
D.0 |
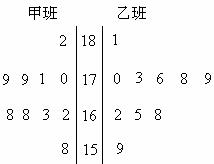
6. 随机抽取某中学甲,乙两班各10名同学,测量他们的身高(单位:cm),获得身高数据的茎叶图如图 ,则下列关于甲,乙两班这10名同学身高的结论正确的是 ( )
|
A. 甲班同学身高的方差较大 |
|
B. 甲班同学身高的平均值较大 |
|
C. 甲班同学身高的中位数较大 |
|
D. 甲班同学身高在175以上的人数较多 |
5. 已知直线 、
、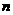 与平面
与平面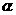 、
、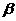 ,下列命题正确的是
( )
,下列命题正确的是
( )
A.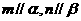 且 且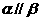 ,则 ,则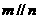 |
B.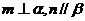 且 且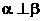 ,则 ,则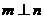 |
C.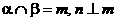 且 且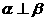 ,则 ,则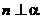 |
D.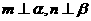 且 且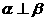 ,则 ,则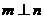 |
4. 若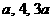 为等差数列的连续三项,则
为等差数列的连续三项,则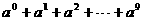 的值为( )
的值为( )
|
A.2047 |
B.1062 |
C.1023 |
D.531 |
3. 设双曲线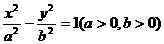 的虚轴长为2,焦距为
的虚轴长为2,焦距为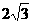 ,则双曲线的渐近线方程为( )
,则双曲线的渐近线方程为( )
A. 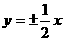 |
B.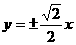 |
C.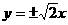 |
D. 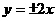 |
2. 若函数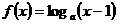
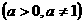 的图像恒过定点,则定点的坐标为 ( )
的图像恒过定点,则定点的坐标为 ( )
A.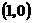 |
B. 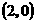 |
C.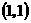 |
D.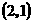 |
1. 若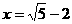 ,
,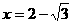 ,则
,则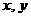 满足 ( )
满足 ( )
A.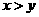 |
B.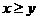 |
C.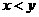 |
D.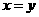 |
1. 绝对值 例1 (1986年扬州初一竞赛题)设T=|x-p|+|x-15|+|x-p-15|,其中0<p<15.对于满足p≤x≤15的x的来说,T的最小值是多少? 解由已知条件可得 T=(x-p)+(15-x)+(p+15-x)=30-x. ∵当p≤x≤15时,上式中在x取最大值时T最小;当x=15时,T=30-15=15,故T的最小值是15. 例2 若两数绝对值之和等于绝对值之积,且这两数都不等于0.试证这两个数都不在-1与-之间. 证 设两数为a、b,则|a|+|b|=|a||b|. ∴|b|=|a||b|-|a|=|a|(|b|-1). ∵ab≠0,∴|a|>0,|b|>0. ∴|b|-1=>0,∴|b|>1. 同理可证|a|>1. ∴a、b都不在-1与1之间. 例3 设a、b是实数,证明 |a|-|b|≤|a+b|≤|a|+|b|. 证明 当|a|-|b|≤0时,|a|-|b|≤|a+b|成立. 当|a|-|b|>0时,由于 (|a|-|b|)2-|a+b|2 =(a2+b2-2|ab|)-(a2+b2+2ab) =-2(|ab|-ab)≤0, ∴|a|-|b|≤|a+b|. 同理可证|a+b|≤|a|+|b|. 2. 根式 在根式进行化简、求值和证明的过程中,常采用配方法、乘方法、比较系数法、设参法、公式法等等,现举例如下: (1) 配方法:将二次根号内的式子配成完全平方式,将三次根号下的式子配成完全立方式. 例4 (1981年宁波初中竞赛题)设的整数部分为x,小数部分为y,试求的值. 解 =4-=2+(2-), 故x=2,y=2-, ∴x+y+ =4-+2+=6. 例5 化简 解 原式= =|x+3|+|x-1|-|x-2|. 令x+3=0,x-1=0,x-2=0.得x=-3,x=1,x=2,这些点把数轴划分成四个部分: 当x<-3时 原式=-(x+3)-(x-1)+(x-2)=-x-4; 当-3≤x<1时, 原式=(x+3)-(x-1)+(x-2)=x+2; 当1≤x≤2时, 原式=(x+3)+(x-1)+(x-2)=3x; 当x>2时, 原式=(x+3)+(x-1)-(x-2)=x+4. 说明:将根号下含字母的式子化为带绝对值的式子来讨论,是解这类问题的一般技巧. 例6 化简(a>>0). 解 原式= = = ∵a>>0. ∴a2>2b2, ∴原式= 例7 求证: 证明:∵ = ∴原式=4. (2)乘方法:由于乘方与开方互为逆运算,顺理成章地可以用乘方的方法去根号 例8 已知求证: (x+y+z)3=27xyz. 证明:∵ ∴ 两边立方 x+y+ 即 再边再立方得(x+y+z)3=27xyz. 例9 已知 求证 证明 设则 即 同理可设则 ∴A+B= = = 由 A+B=a, 得 ∴ (2) 比较系数法 例10 求满足条件的自然数a、x、y. 解 将等式两边平方得 ∵x、y、a都是自然数. ∴只能是无理数,否则与等式左边是无理数相矛盾. ∴x+y=a,xy=6. 由条件可知 x>y且x、y是自然数. 当x=6时,y=1,得a=7. 当x=3时,y=2,得a=5. 故x=6,y=1,a=7. 或x=3,y=2,a=5. 例11 化简 分析 被开方式展开后得13+2,含有三个不同的根式,且系数都是2,可看成是将平方得来的. 解 设 =, 两边平方得 13+2 =x+y+z+2 比较系数,得 ①②③④ 由②有,代入③,得代入④,得y2=52,∴y=5(x、y、z非负), ∴=1, ∴原式=1+ (4)设参法 例12 (1986年数理化接力赛题) 设(a1,a2,…,an,b1,b2,…,bn都是正数).求证: = 证明 设 且a1=b1k,a2=b2k,…,an=bnk. 左边= = 右边= · = ∴左边=右边 (5)公式法、代数变换及其他 例13 已知x=求x3+12x的值. 解 由公式(a-b)3=a3-b3-3ab(a-b)可得 · =8-3 =8-12x. ∴x3+12x=8. 例14 设 求x4+y4+(x+y)4. 解 由条件知 ∴x+y=5,xy=1. ∴原式=(x2+y2)2-2x2y2+(x+y)4 =[(x+y)2-2xy]2-2x2y2+(x+y)4 =(25-2)2-2+54 =1152. 例15 (1978年罗马尼亚竞赛题)对于a∈R,确定的所有可能的值. 解 记y=. ① 先假定a≥0,这时y≥0,把①两边平方得 ② 即 ③ 再平方,整理后得 ④ 从而 ≥0. 由②知 y2<2a2+2-2=2. 再由⑤知 y2≤1,∴0≤y<1. 反过来,对于[0,1]中的每一个y值,由⑤可以定出a,并且这时2a2+2-y2>0,故可由⑤逆推出②和①,因而在a≥0时,的值域为(0,1). 同样在a<0时,的值域为(-1,0),综上的值域是(-1,1). 练习十七 1. 选择题 (1)若实数x满足方程|1-x|=1+|x|,那么等于( ). (A)x-1(B)1-x(C)±(x-1)(D)1(E)-1 (2)方程x|x|-5|x|+6=0的最大根和最小根的积为( ). (A)-6 (B)3 (C)-3 (D)6 (E)-18 (3)已知最简根式与是同类根式,则满足条件的a、b的值( ). (A) 不存在 (B)有一组 (C)有二组 (D)多于二组 2. 空题 (1) 已知|x-8y|+(4y-1)2+则x+y+z=_________. (2) 若a>b>c>0,l1=乘积中最小的一个是__________. (3) 已知0<x<1,化简 (4) 已知则 (5)(北京市1989年高一数学竞赛题)设x是实数,且f(x)=|x+1|+|x+2|+|x+3|+|x+4|+|x+5|.则f(x)的最小值等于__________. 3.化简(a>0). 4.已知ab<0,a2+b2=a2b2,化简 5.如果x>0,y>0,且试求的值. 6.(第8届美国教学邀请赛试题) 求的值. 7.求适合下列各式的x、y; (1)若x、y为有理数,且 (2)若x、y为整数, 8.已知求证a2+b2=1. 9.已知A=求证 11<A3-B3<12<A3+B3<13. 10.(1985年武汉初二数学竞赛题)已知其中a、b都是正数. (1) 当b取什么样的值时,的值恰好为b? (2) 当b取什么样的值时,的值恰好为? 练习十七 1.略 2.(1)3 (2)l (3)2x (4)a2-2 (5)6. 3.当时,y=a,当x>2a2时,y= 4.∵ab<0,∴|ab|=-ab,若a>0>b,原式=-ab;若a<0<b,原式=ab. 5.原式=2. 6.原式=828. 7.(1) (2)x=22,y=2;x=-22,y=-2. 8.由条件知两边平方后整理得再平方得1-2b2-2a2+b4+2a2b2+a4=0即1-2(a2+b2)+(a2+b2)2=0,[1-(a2+b2)]2=0,∴a2+b2=1. 9.∵A2+B2=6,AB=2,∴(A+B)2=1,A+B=,A-B=,∴A3-B3=(A-B)+3AB(A-B)= 8.当b≥0时,原式值为b, 当0<b<1时,原式值为
22、
已知函数f(x)=x+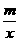 ,且f(1)=2.
,且f(1)=2.
(1)求m;
(2)判断f(x)的奇偶性;
(3)函数f(x)在(1,+∞)上是增函数还是减函数?并证明.
解:(1)f(1):1+m=2,m=1.
(2)f(x)=x+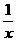 ,f(-x)=-x-
,f(-x)=-x-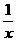 =-f(x),∴f(x)是奇函数.
=-f(x),∴f(x)是奇函数.
(3)设x1、x2是(1,+∞)上的任意两个实数,且x1<x2,则
f(x1)-f(x2)=x1+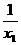 -(x2+
-(x2+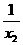 )=x1-x2+(
)=x1-x2+(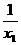 -
-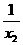 )
)
=x1-x2-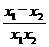 =(x1-x2)
=(x1-x2)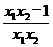 .
.
当1<x1<x2时,x1x2>1,x1x2-1>0,从而f(x1)-f(x2)<0,
即f(x1)<f(x2).
∴函数f(x)=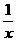 +x在(1,+∞)上为增函数.
+x在(1,+∞)上为增函数.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com