
题目列表(包括答案和解析)
19. 对于给定数列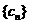 ,如果存在实常数
,如果存在实常数 使得
使得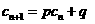 对于任意
对于任意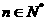 都成立,我们称数列
都成立,我们称数列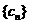 是 “M类数列”.
是 “M类数列”.
(1)若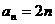 ,
,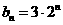 ,
,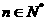 ,数列
,数列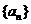 、
、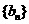 是否为“M类数列”?若是,指出它对应的实常数
是否为“M类数列”?若是,指出它对应的实常数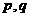 ,若不是,请说明理由;
,若不是,请说明理由;
(2)证明:若数列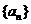 是“M类数列”,则数列
是“M类数列”,则数列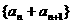 也是“M类数列”;
也是“M类数列”;
(3)若数列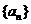 满足
满足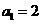 ,
,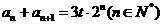 ,
,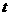 为常数.求数列
为常数.求数列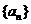 前
前 项的和.并判断
项的和.并判断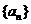 是否为“M类数列”,说明理由;
是否为“M类数列”,说明理由;
(4)根据对(2)(3)问题的研究,对数列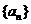 的相邻两项
的相邻两项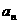 、
、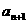 ,提出一个条件或结论与“M类数列”概念相关的真命题,并探究其逆命题的真假.
,提出一个条件或结论与“M类数列”概念相关的真命题,并探究其逆命题的真假.
18. 在平面直角坐标系 中,已知圆
中,已知圆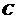 的圆心在第二象限,半径为
的圆心在第二象限,半径为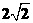 且与直线
且与直线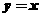 相切于原点
相切于原点 .椭圆
.椭圆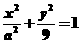 与圆
与圆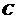 的一个交点到椭圆两焦点的距离之和为
的一个交点到椭圆两焦点的距离之和为 .
.
(1)求圆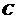 的方程;
的方程;
(2)圆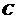 上是否存在点
上是否存在点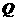 ,使
,使 关于直线
关于直线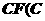 为圆心,
为圆心,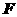 为椭圆右焦点)对称,若存在,请求出点
为椭圆右焦点)对称,若存在,请求出点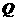 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
17. 某商品每件成本价80元,售价100元,每天售出100件.若售价降低x成(1成=10%),售出商品数量就增加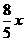 成,要求售价不能低于成本价.
成,要求售价不能低于成本价.
(1)设该商店一天的营业额为y,试求y与x之间的函数关系式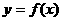 ,并写出定义域;
,并写出定义域;
(2)若再要求该商品一天营业额至少10260元,求x的取值范围.
16.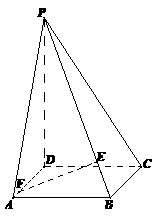 如图,已知四棱锥
如图,已知四棱锥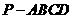 的底面
的底面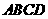 是边长为
是边长为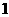 的正方形,
的正方形,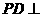 底面
底面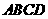 ,且
,且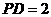 .
.
(1) 若点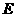 、
、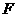 分别在棱
分别在棱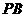 、
、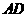 上,且
上,且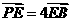 ,
,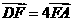 ,求证:
,求证: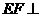 平面
平面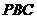 ;
;
(2) 若点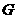 在线段
在线段 上,且三棱锥
上,且三棱锥 的体积为
的体积为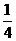 ,试求线段
,试求线段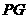 的长.
的长.
15. 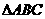 中,三个内角A、B、C所对的边分别为
中,三个内角A、B、C所对的边分别为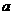 、
、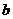 、
、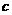 ,若
,若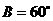 ,
, 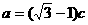 .
.
(1)求角 的大小;
的大小;
(2)已知当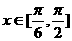 时,函数
时,函数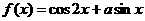 的最大值为3,求
的最大值为3,求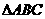 的面积.
的面积.
14. )给出下列命题:(1)三点确定一个平面;(2)在空间中,过直线外一点只能作一条直线与该直线平行;(3)若平面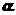 上有不共线的三点到平面
上有不共线的三点到平面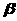 的距离相等,则
的距离相等,则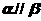 ;(4)若直线
;(4)若直线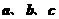 满足
满足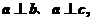 则
则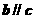 .其中正确命题的个数是_____________
.其中正确命题的个数是_____________
13. 在实数数列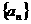 中,已知
中,已知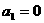 ,
,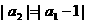 ,
, ,…,
,…,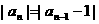 ,则
,则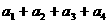 的最大值为_____________
的最大值为_____________
12. 已知函数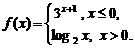 若
若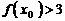 ,则
,则 的取值范围是_____________
的取值范围是_____________
11. 在一个水平放置的底面半径为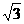 cm的圆柱形量杯中装有适量的水,现放入一个半径为
cm的圆柱形量杯中装有适量的水,现放入一个半径为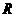 cm的实心铁球,球完全浸没于水中且无水溢出,若水面高度恰好上升
cm的实心铁球,球完全浸没于水中且无水溢出,若水面高度恰好上升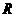 cm,则
cm,则 ________cm.
________cm.
10. 设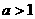 ,若仅有一个常数c使得对于任意的
,若仅有一个常数c使得对于任意的 ,都有
,都有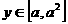 满足方程
满足方程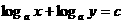 ,这时,
,这时,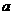 的取值的集合为
的取值的集合为


湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com