
题目列表(包括答案和解析)
21.(本题满分12分)
解:(Ⅰ)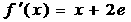 ,
,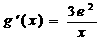 ………………1分
………………1分
设函数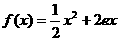 与
与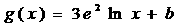 的图象有公共点为
的图象有公共点为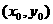
由题意得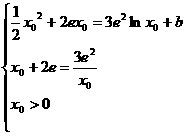 ………………………3分
………………………3分
解得: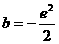 ………………………5分
………………………5分
(Ⅱ)由(Ⅰ)知,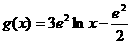
所以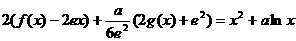
即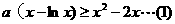
当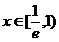 时,
时,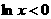 ,
,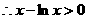
当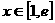 时,
时,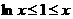 ,且等号不能同时成立,
,且等号不能同时成立,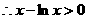
所以,则由(1)式可得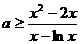 在
在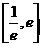 上恒成立……………………7分
上恒成立……………………7分
设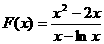 ,
,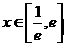
又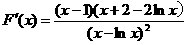 ……………………9分
……………………9分
令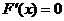 得:
得: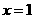
又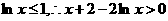
所以,当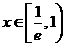 时,
时,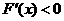 ;当
;当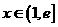 时,
时,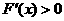 ;
;
所以,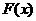 在
在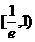 上为减函数,
上为减函数,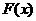 在
在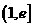 上为增函数…………11分
上为增函数…………11分
又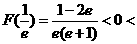
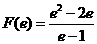
故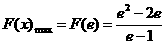
所以实数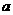 的取值范围是
的取值范围是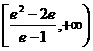 ……………12分
……………12分
20.(本题满分12分)
解:(Ⅰ)因为 ,即
,即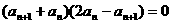
又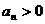 ,所以有
,所以有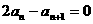 ,所以
,所以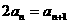
所以数列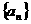 是公比为
是公比为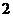 的等比数列…………2分
的等比数列…………2分
由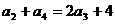 得
得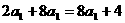 ,解得
,解得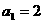
故数列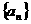 的通项公式为
的通项公式为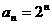
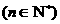 …………4分
…………4分
(Ⅱ) 因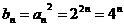 ,所以
,所以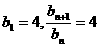
即数列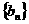 是首项为
是首项为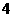 ,公比是
,公比是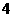 的等比数列
的等比数列
所以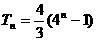 …………6分
…………6分
则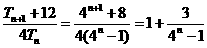
又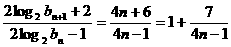
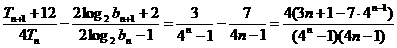
猜想: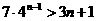 …………8分
…………8分
①当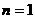 时,
时, ,上面不等式显然成立;
,上面不等式显然成立;
②假设当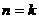 时,不等式
时,不等式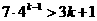 成立…………9分
成立…………9分
当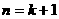 时,
时,
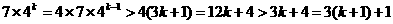
综上①②对任意的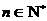 均有
均有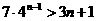 …………11分
…………11分
又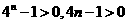
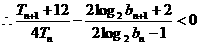
所以对任意的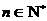 均有
均有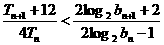 …………12分
…………12分
19.(本题满分12分)
解: 由题意知: 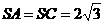 ,侧面
,侧面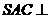 底面
底面 ,
,
 底面
底面 为正三角形…………2分
为正三角形…………2分
(Ⅰ) 取 的中点
的中点 ,连结
,连结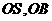 .
.
因为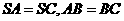 ,
,
所以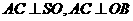 .
.
所以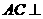 平面
平面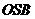 .
.
所以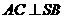 …………4分
…………4分
(Ⅱ) 如图所示建立空间直角坐标系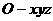 ,
,
则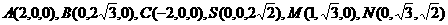 .
.
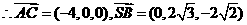 .
.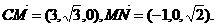 …………6分
…………6分
设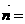
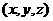 为平面
为平面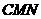 的一个法向量,
的一个法向量,
则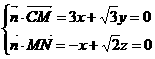 ,取
,取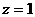 ,得
,得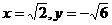 .
.
所以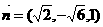 …………8分
…………8分
又由上可得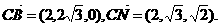
设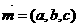 为平面
为平面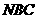 的法向量,
的法向量,
由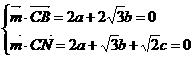 ,得
,得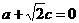 ,
,
令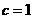 ,则
,则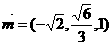 …………10分
…………10分
所以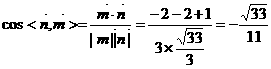
所以二面角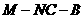 的余弦值为
的余弦值为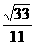 . …………12分
. …………12分
18.(本小题满分12分)
解: (Ⅰ)选出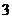 种商品一共有
种商品一共有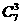 种选法, …………2分
种选法, …………2分
选出的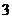 种商品中至多有一种是家电商品有
种商品中至多有一种是家电商品有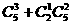 种. …………4分
种. …………4分
所以至多有一种是家电商品的概率为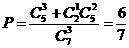 .…………5分
.…………5分
(Ⅱ)奖券总额是一随机变量,设为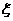 ,可能值为
,可能值为 ,
, 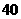 ,
,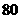 ,
,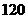 .…………6分
.…………6分
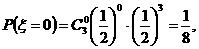 …………7分
…………7分
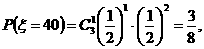 …………8分
…………8分
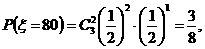 …………9分
…………9分
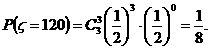 …………10分
…………10分
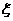 |
0 |
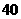 |
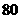 |
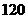 |
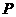 |
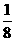 |
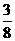 |
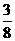 |
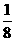 |
所以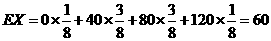 .
.
所以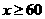 ,因此要使促销方案对商场有利,则
,因此要使促销方案对商场有利,则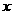 最少为
最少为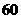 元. …………12分
元. …………12分
17.(本小题满分12分)
解: (Ⅰ)由题意得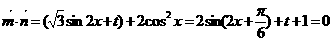 …………3分
…………3分
所以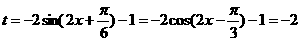 …………………6分
…………………6分
(Ⅱ)由(Ⅰ)知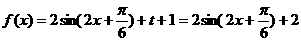
由题意得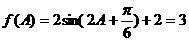
所以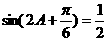 …………………8分
…………………8分
因为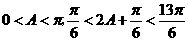 ,所以
,所以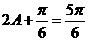
解得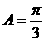
因为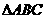 的面积为
的面积为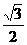 ,所以
,所以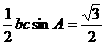 ,
,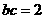 即
即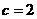 …………10分
…………10分
由余弦定理得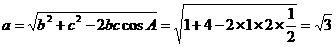 …………12分
…………12分
22.(本题满分14分)
已知椭圆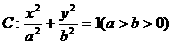 的左右两焦点分别为
的左右两焦点分别为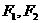 ,
,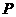 是椭圆
是椭圆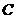 上的一点,且在
上的一点,且在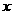 轴的上方,
轴的上方,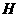 是
是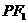 上一点,若
上一点,若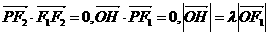 ,
,
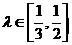 (其中
(其中 为坐标原点).
为坐标原点).
(Ⅰ)求椭圆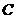 离心率
离心率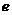 的最大值;
的最大值;
(Ⅱ)如果离心率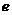 取(Ⅰ)中求得的最大值, 已知
取(Ⅰ)中求得的最大值, 已知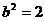 ,点
,点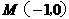 ,设
,设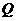 是椭圆
是椭圆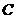 上的一点,过
上的一点,过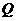 、
、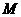 两点的直线
两点的直线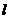 交
交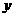 轴于点
轴于点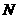 ,若
,若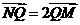 , 求直线
, 求直线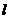 的方程.
的方程.
[2010青岛一模]答案
21.(本题满分12分)
已知定义在正实数集上的函数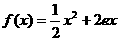 ,
,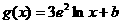 (其中
(其中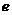 为常数,
为常数,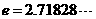 ),若这两个函数的图象有公共点,且在该点处的切线相同.
),若这两个函数的图象有公共点,且在该点处的切线相同.
(Ⅰ)求实数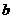 的值;
的值;
(Ⅱ)当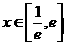 时,
时,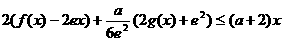 恒成立,求实数
恒成立,求实数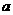 的取值范围.
的取值范围.
20.(本题满分共12分)
已知各项均为正数的数列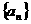 满足
满足 ,且
,且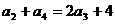 ,其中
,其中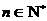 .
.
(Ⅰ)求数列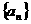 的通项公式;
的通项公式;
(Ⅱ)设数列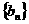 的前
的前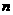 项和为
项和为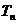 ,令
,令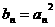 ,其中
,其中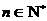 ,试比较
,试比较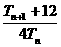 与
与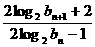 的大小,并加以证明.
的大小,并加以证明.
19.(本题满分共12分)
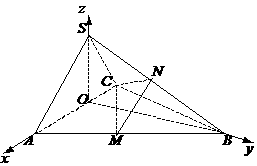
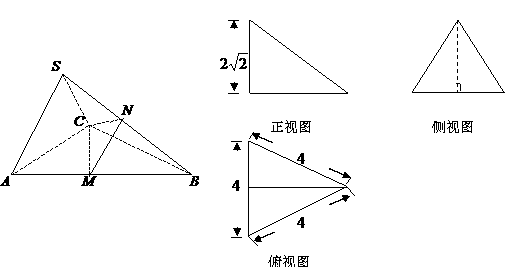
下图分别为三棱锥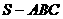 的直观图与三视图,在直观图中,
的直观图与三视图,在直观图中,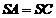 ,
,
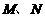 分别为
分别为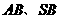 的中点.
的中点.
(Ⅰ)求证: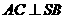 ;
;
(Ⅱ)求二面角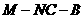 的余弦值.
的余弦值.
18.(本小题满分12分)
某商场准备在国庆节期间举行促销活动,根据市场调查,该商场决定从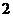 种服装商品,
种服装商品, 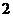 种家电商品,
种家电商品,
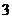 种日用商品中,选出
种日用商品中,选出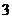 种商品进行促销活动.
种商品进行促销活动.
(Ⅰ)试求选出的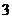 种商品中至多有一种是家电商品的概率;
种商品中至多有一种是家电商品的概率;
(Ⅱ)商场对选出的某商品采用的促销方案是有奖销售,即在该商品现价的基础上将价格提高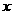 元,同时,若顾客购买该商品,则允许有
元,同时,若顾客购买该商品,则允许有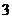 次抽奖的机会,若中奖,则每次中奖都获得数额为
次抽奖的机会,若中奖,则每次中奖都获得数额为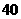 元的奖券.假设顾客每次抽奖时获奖的概率都是
元的奖券.假设顾客每次抽奖时获奖的概率都是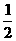 ,若使促销方案对商场有利,则
,若使促销方案对商场有利,则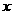 最少为多少元?
最少为多少元?
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com