
题目列表(包括答案和解析)
19.(本小题满分12分)
设等差数列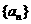 的前
的前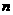 项和为
项和为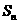 ,公比是正数的等比数列
,公比是正数的等比数列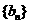 的前
的前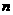 项和为
项和为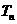 ,已知。
,已知。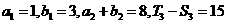
(Ⅰ)求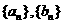 的通项公式;
的通项公式;
(Ⅱ)若数列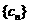 满足
满足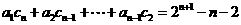 对任意
对任意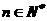 都成立;求证:数列
都成立;求证:数列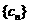 是等比数列。
是等比数列。
18.(本小题满分12分)
某校举行了“环保知识竞赛”,为了解本次竞赛成 频率分布表
|
分组 |
频数 |
频率 |
|
[50,60) |
5 |
0.05 |
|
[60,70) |
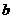 |
0.20 |
|
[70,80) |
35 |
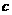 |
|
[80,90) |
30 |
0.30 |
|
[90,100) |
10 |
0.10 |
|
合计 |
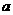 |
1.00 |
绩情况,从中随机抽取部分学生的成绩(得分均为整数,
满分100分),进行统计,请根据频率分布表中所提供
的数据,解答下列问题:
(Ⅰ)求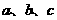 的值及随机抽取一考生其成绩不
的值及随机抽取一考生其成绩不
低于70分的概率;
(Ⅱ)按成绩分层抽样抽取20人参加社区志愿者活
动,并从中指派2名学生担任负责人,记这2名学生中
“成绩低于70分”的人数为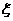 ,求
,求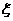 的分布列及期望。
的分布列及期望。
17.(本小题满分12分)
已知函数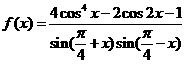
(Ⅰ)求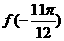 的值;
的值;
(Ⅱ)当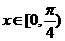 时,求g
时,求g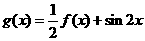 的最大值和最小值。
的最大值和最小值。
22.解:(1)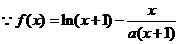
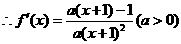
 函数
函数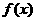 在[0,+∞)恒成立 2分
在[0,+∞)恒成立 2分
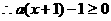 对任意
对任意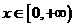 恒成立,
恒成立,
即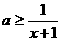 对任意
对任意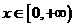 恒成立 3分
恒成立 3分
而当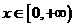 时,
时,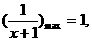
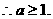 4分
4分
(2)当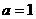 ,
,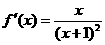
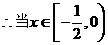 时,
时,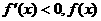 在
在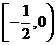 上单调递减, 5分
上单调递减, 5分
当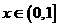 时,
时,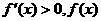 在(0,1]上单调递增 6分
在(0,1]上单调递增 6分
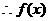 在
在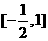 上有唯一极小值点。
上有唯一极小值点。
故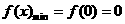 7分
7分
又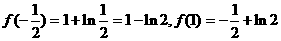 8分
8分
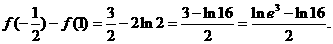
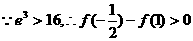 ,
,
即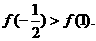 9分
9分
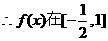 上的最大值为
上的最大值为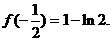
综上,函数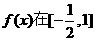 上的最大值是
上的最大值是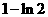 ,最小值是0。 10分
,最小值是0。 10分
(3)法一:用数学归纳法。
①当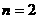 时,要证
时,要证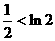 ,只要证
,只要证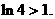 显然成立。 11分
显然成立。 11分
②假设当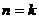 时,
时,
不等式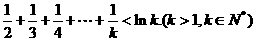 成 立
成 立
则当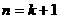 时,
时,
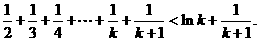 12分
12分
要证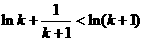 成立,
成立,
只要证 ,
,
即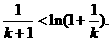
令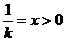 ,则上式化为
,则上式化为
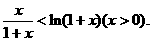
只要证: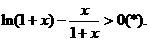
由(1)知,当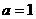 时,
时,
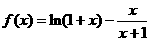 在[0,+∞)内是增函数,
在[0,+∞)内是增函数,
故有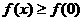 ,
,
好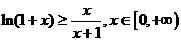 成立,
成立,
而(*)中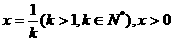
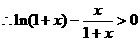 ,即(*)式成立,
,即(*)式成立,
 当
当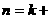 1时,不等式成立,
1时,不等式成立,
由①②知对任意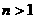 的正整数不等式都成立。 14分
的正整数不等式都成立。 14分
法二:由(1)知,当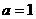 时,
时,
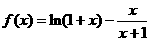 在[0,+∞)上是增函数,
在[0,+∞)上是增函数,
故有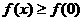 ,
,
即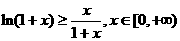 成立。 11分
成立。 11分
令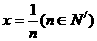 ,
,
则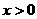
 有
有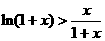 ,
,
即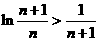 12分
12分
由此得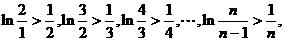
则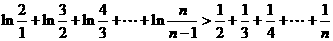 13分
13分
即得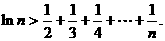
故对大于1的任意正整数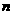 ,都有
,都有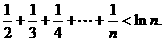 14分
14分
21. 解(1)由题意,设抛物线为
解(1)由题意,设抛物线为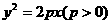 1分
1分
由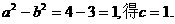 2分
2分
 抛物线的焦点为(1,0)
抛物线的焦点为(1,0)
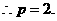 3分
3分
 抛物线C的方程为
抛物线C的方程为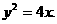 4分
4分
(2)当斜率存在时,设直线为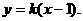 5分
5分
联立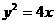 ,消去
,消去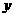
得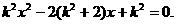
则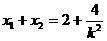 ,
,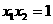
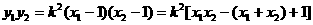
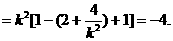
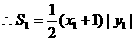
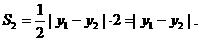
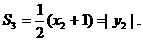 8分
8分
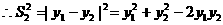
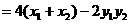
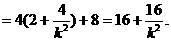 9分
9分
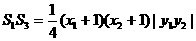
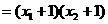
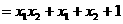
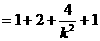
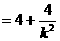 10分
10分
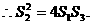
当斜率不存在时,直线为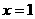 ,
,
可求得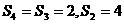 ,亦有
,亦有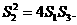 11分
11分
故存在实数4,使得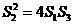 成立。 12分
成立。 12分
20.解:(1)因为直接受A感染的人至少是B,而C、D二人也有可能是由A感染的,
所以X=1,2,3
设B、C、D直接受A感染为事件B、C、D,
则B、C、D是相互独立的,
并且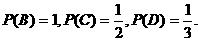
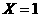 ,表明除了B外,C、D都不是由A感染的,
,表明除了B外,C、D都不是由A感染的,
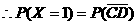
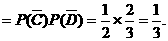 2分
2分
X=2,表明除了B外,C、D二人中恰有1人是由A感染的,
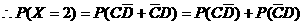
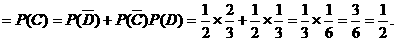 4分
4分
X=3,表明B、C、D都是由A感染的,
所以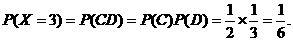 5分
5分
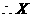 的分布列为:
的分布列为:
|
X |
1 |
2 |
3 |
|
P |
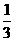 |
 |
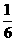 |
……6分
同理,Y的分布列为:
|
Y |
1 |
2 |
3 |
|
P |
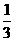 |
 |
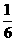 |
……8分
Z的分布列为:
|
Z |
0 |
1 |
|
P |
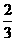 |
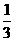 |
……10分
(2)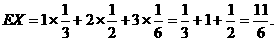 11分
11分
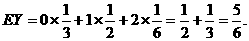
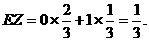
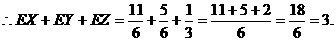 12分
12分
19.解:(1)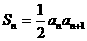
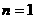 时,
时,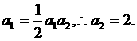 1分
1分
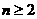 时,
时,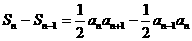
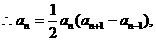 3分
3分
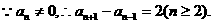 4分
4分
令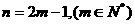
得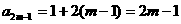
令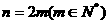
得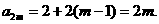
故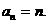 6分
6分
(2)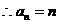
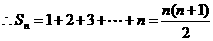 7分
7分
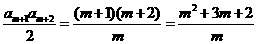
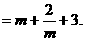 8分
8分
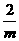 必为正整数,
必为正整数,
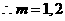 9分
9分
当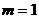 时,
时,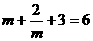
由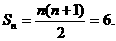
得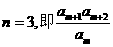 为数列
为数列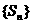 中第3项 11分
中第3项 11分
故所求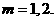 12分
12分
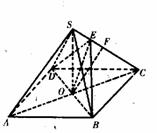
18.解:(1)连结BD,AC,
设BD与AC交于O。 1分
由底面是菱形,得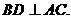 2分
2分
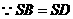 ,O为BD中点
,O为BD中点
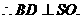 3分
3分
又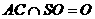 ,
,
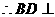 面SAC 4分
面SAC 4分
又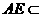 面SAC,
面SAC,
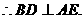 5分
5分
(2)取SC的中点F,连结OF,OE,
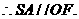
 与平面EDB所成的角就是SA与平面EDB所成的角 6分
与平面EDB所成的角就是SA与平面EDB所成的角 6分
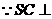 平面BED,
平面BED,
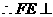 面BED,E为垂足,
面BED,E为垂足,

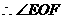 为所求角 7分
为所求角 7分
在等腰 中,
中,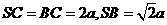
得底边SB上的高为
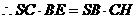
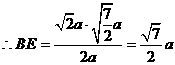 9分
9分
 在
在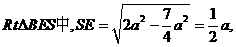
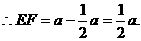 10分
10分
在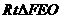 中,
中,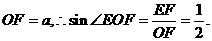 11分
11分
即直线SA与平面BED所成角为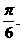 12分
12分
(2)法二:由(1)知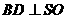 ,
,
同理可证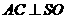 ,
,
 平面AC,
平面AC,
取AC和BD的交点O为原点建立如图所示的坐标系,
设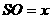 ,
,
则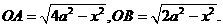
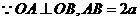 ,
,
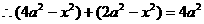
解得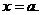
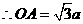 ,
,
则A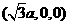
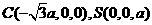 7分
7分
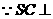 平面EBD,
平面EBD,
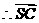 是平面EBD的法向量。
是平面EBD的法向量。
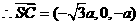
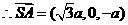
设SA与平面BED所成角为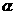 ,则
,则
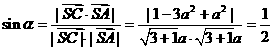 11分
11分
即SA与平面BED所成的角为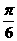
17.(满分12分)
解:(1)设最高点为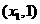 ,相邻的最低点为
,相邻的最低点为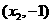 ,则
,则
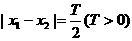 2分
2分
由其图象得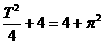
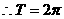 3分
3分
由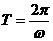 ,得
,得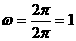
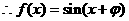 4分
4分
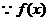 是偶函数,
是偶函数,
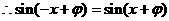 ,
,
得
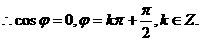
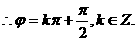 5分
5分
又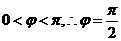 ,
,
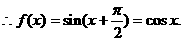 6分
6分
注:由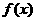 是偶函数, 直接得
是偶函数, 直接得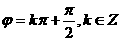 的不扣分。
的不扣分。
(2)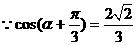
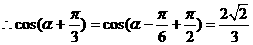 7分
7分
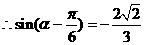 8分
8分
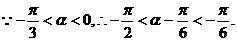 9分
9分
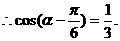 10分
10分
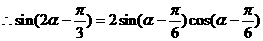 11分
11分
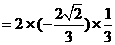
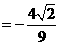 12分
12分
22.(本小题满分14分)
已知函数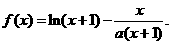
(1)若函数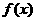 在[0,+∞)内为增函数,求正实数
在[0,+∞)内为增函数,求正实数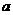 的取值范围;
的取值范围;
(2)当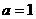 时,求
时,求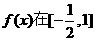 上的最大值和最小值;
上的最大值和最小值;
(3)试利用(1)的结论,证明:对于大于1的任意正整数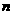 ,都有
,都有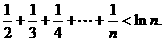
[2010临沂一模]答案
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com