
题目列表(包括答案和解析)
21.(本小题满分12分)
已知定点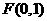 和直线
和直线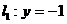 ,过定点F与直线
,过定点F与直线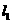 相切的动圆圆心为点C。
相切的动圆圆心为点C。
(1)求动点C的轨迹方程;
(2)过点F在直线l2交轨迹于两点P、Q,交直线l1于点R,求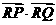 的最小值。
的最小值。
20.(本小题满分12分)
济南市有大明湖、趵突泉、千佛山、园博园4个旅游景点,一位客人浏览这四个景点的概率分别是0.3,0.4,0.5,0.6,且客人是否游览哪个景点互不影响,设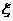 表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。
表示客人离开该城市时游览的景点数与没有游览的景点数之差的绝对值。
(1)求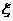 =0对应的事件的概率;
=0对应的事件的概率;
(2)求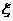 的分布列及数学期望。
的分布列及数学期望。
19.(本小题满分12分)
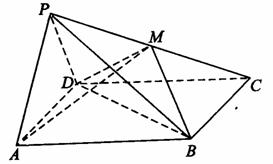 如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA//平面BDM,
如图,在四棱锥P-ABCD中,侧面PAD是正三角形,且垂直于底面ABCD,底面ABCD是边长为2的菱形,∠BAD=60°,M为PC上一点,且PA//平面BDM,
(1)求证:M为PC的中点;
(2)求证:面ADM⊥面PBC。
18.(本小题满分12分)
已知数列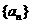 的各项为正数,前
的各项为正数,前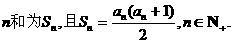
(1)求证:数列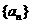 是等差数列;
是等差数列;
(2)设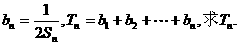
17.(本小题满分12分)
已知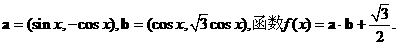
(1)求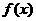 的最小正周期,并求其图象对称中心的坐标;
的最小正周期,并求其图象对称中心的坐标;
(2)当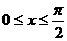 时,求函数
时,求函数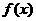 的值域。
的值域。
22.解:(1)由题意,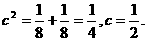
所以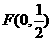 ,抛物线D的标准方程为
,抛物线D的标准方程为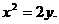 …………3分
…………3分
(2)设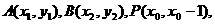
由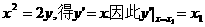
抛物线D在点A处的切线方程为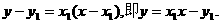 …………4分
…………4分
而A点处的切线过点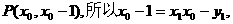
即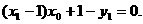
同理,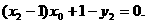
可见,点A,B在直线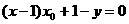 上.
上.
令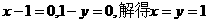
所以,直线AB过定点Q(1,1) …………6分
(3)设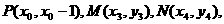
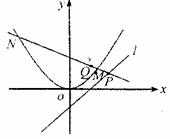 直线PQ的方程为
直线PQ的方程为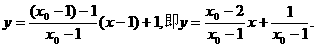
由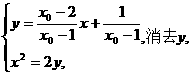
得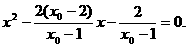
由韦达定理,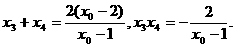 …………9分
…………9分
而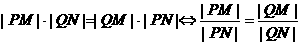
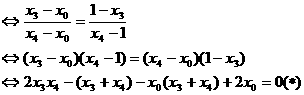
…………12分
将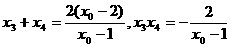 代入方程(*)的左边,得
代入方程(*)的左边,得
(*)的左边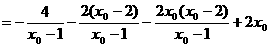
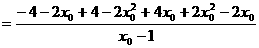
=0.
因而有|PM|·|QN|=|QM|·|PN|. …………14分
[2010济南一模]
21.(1)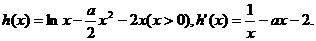
若使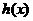 存在单调递减区间,则
存在单调递减区间,则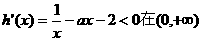 上有解.……1分
上有解.……1分
而当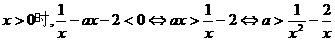
问题转化为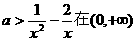 上有解,故a大于函数
上有解,故a大于函数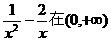 上的最小值.
上的最小值.
………………3分
又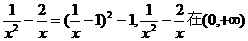 上的最小值为-1,所以a>1.……4分
上的最小值为-1,所以a>1.……4分
(2)令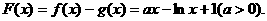
函数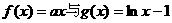 的交点个数即为函数
的交点个数即为函数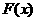 的零点的个数.……5分
的零点的个数.……5分
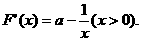
令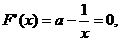 解得
解得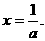
随着x的变化,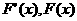 的变化情况如下表:
的变化情况如下表:
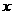 |
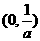 |
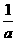 |
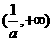 |
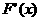 |
- |
0 |
+ |
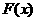 |
单调递减 |
极(最)小值2+lna |
单调递增 |
…………7分
①当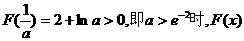 恒大于0,函数
恒大于0,函数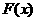 无零点.……8分
无零点.……8分
②当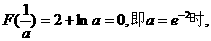 由上表,函数
由上表,函数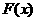 有且仅有一个零点.
有且仅有一个零点.
……9分
③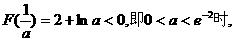 显然
显然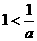
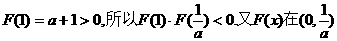 内单调递减,
内单调递减,
所以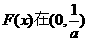 内有且仅有一个零点 …………10分
内有且仅有一个零点 …………10分
当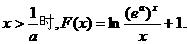
由指数函数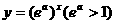 与幂函数
与幂函数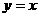 增长速度的快慢,知存在
增长速度的快慢,知存在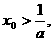
使得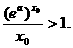
从而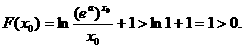
因而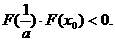
又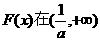 内单调递增,
内单调递增,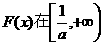 上的图象是连续不断的曲线,
上的图象是连续不断的曲线,
所以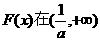 内有且仅有一个零点. …………11分
内有且仅有一个零点. …………11分
因此,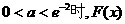 有且仅有两个零点.
有且仅有两个零点.
综上,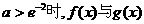 的图象无交点;当
的图象无交点;当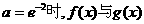 的图象有且仅有一个交点;
的图象有且仅有一个交点;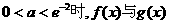 的图像有且仅有两个交点.……12分
的图像有且仅有两个交点.……12分
20.(1)当n=1时,有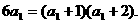
解得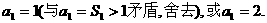 …………1分
…………1分
当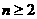 时,有
时,有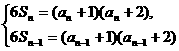 两式相减得
两式相减得
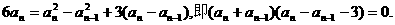 …………3分
…………3分
由题设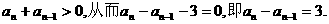
故数列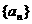 是首项为2,公差为3的等差数列
是首项为2,公差为3的等差数列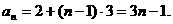 ……5分
……5分
(2)由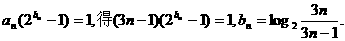 …………6分
…………6分
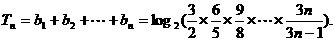
而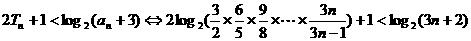
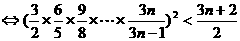
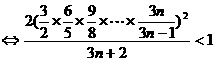 …………8分
…………8分
令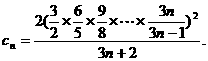
则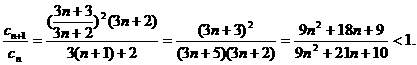
而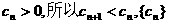 是单调递减数列.…………10分
是单调递减数列.…………10分
所以,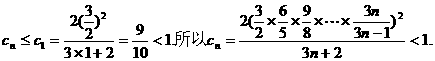
从而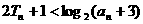 成立. …………12分
成立. …………12分
19.解:以D为从标原点,DC、DA、DP所在直线分别为x轴、y轴、z轴,建立空间直角坐标系D-xyz.设AB=a,则A(0,2,0),B(a,2,0),
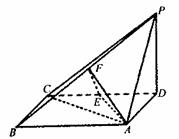 C(a,0,0),D(0,0,0,),p(0,0,2),
C(a,0,0),D(0,0,0,),p(0,0,2),
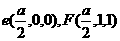 …………2分
…………2分
(1)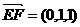
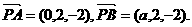
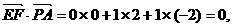
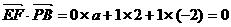
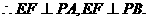
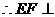 平面PAB. ………………6分
平面PAB. ………………6分
(2)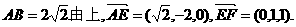
设平面AEF的法向量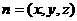 ,
,
则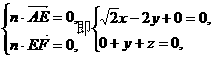
令y=1,则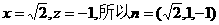 …………9分
…………9分
又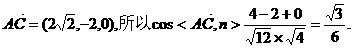 …………11分
…………11分
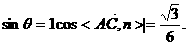 …………12分
…………12分
18.(本小题满分12分)
解:(1)记“第一次摸出3号球”为事件A,“第二次摸出2号球”为事件B,则
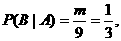 …………4分
…………4分
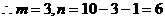 …………5分
…………5分
(2)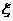 的可能的取值为3,4,5,6. …………6分
的可能的取值为3,4,5,6. …………6分
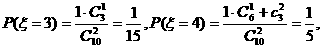
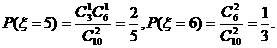 …………10分
…………10分
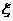 的分布列为
的分布列为
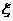 |
3 |
4 |
5 |
6 |
|
P |
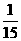 |
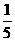 |
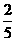 |
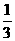 |
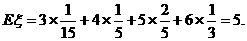 …………12分
…………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com