
题目列表(包括答案和解析)
7. 在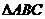 中, 角
中, 角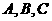 的对边分别为
的对边分别为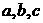 .已知
.已知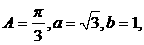 则
则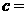
A.1 B.2 C.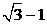 D.
D.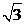
6.  的三内角
的三内角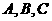 所对边的长分别为
所对边的长分别为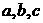 .设向量
.设向量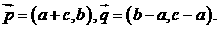 若
若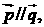 则角
则角 的大小为
的大小为
A.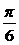 B.
B.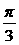 C.
C.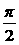 D.
D.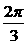
5. 的内角
的内角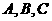 的对边分别为
的对边分别为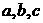 .若
.若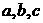 成等比数列,且
成等比数列,且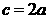 ,则
,则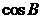 =
A.
=
A.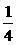 B.
B.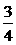 C.
C.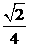 D.
D.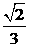
4. 在△ABC中,设命题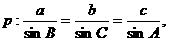 命题q:△ABC是等边三角形,那么命题p是命题q的
命题q:△ABC是等边三角形,那么命题p是命题q的
A.充分不必要条件 B.必要不充分条件 C.充分必要条件 D.既不充分又不必要条件
3.在△ABC中,角A、B、C的对边分别为a、b、c, A=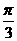 ,a=
,a= ,b=1,则c=
,b=1,则c=
(A) 1
(B)2 (C) -1
(D)
-1
(D)
2. 在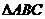 中,
中,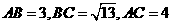 ,则边
,则边 上的高为
上的高为
(A) 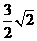 (B)
(B)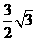 (C)
(C)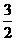 (D)
(D)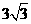
1. △ABC中,a,b,c分别为∠A、∠B、∠C的对边.如果a,b,c成等差数列,∠B=30°,△ABC的面积为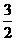 ,那么b= (A)
,那么b= (A)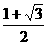 (B)
(B)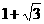 (C)
(C)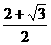 (D)
(D)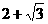
20、(本题满分14分)
解:(Ⅰ)证明:
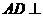 平面
平面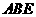 ,
,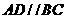 .
.
∴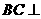 平面
平面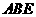 ,则
,则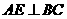 . …… (2分)
. …… (2分)
又
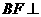 平面
平面 ,则
,则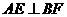 .
.
∴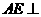 平面
平面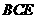 . ……………… (4分)
. ……………… (4分)
(Ⅱ)证明:依题意可知: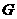 是
是 中点.
中点.

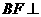 平面
平面 ,则
,则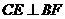 ,而
,而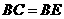 .
.
∴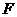 是
是 中点. ……………………(6分)
中点. ……………………(6分)
在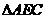 中,
中,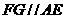 ,∴
,∴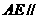 平面
平面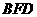 . …………(8分)
. …………(8分)
(Ⅲ)解法一:
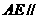 平面
平面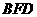 ,∴
,∴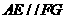 ,而
,而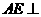 平面
平面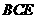 .
.
∴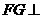 平面
平面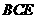 ,∴
,∴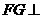 平面
平面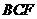 . …………………(9分)
. …………………(9分)

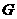 是
是 中点,∴
中点,∴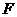 是
是 中点.∴
中点.∴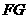
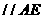 且
且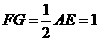 .
.

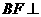 平面
平面 ,∴
,∴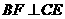 . ………………………(10分)
. ………………………(10分)
∴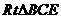 中,
中,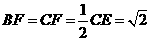 .∴
.∴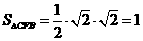 .…(11分)
.…(11分)
∴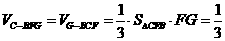 . ……………………(12分)
. ……………………(12分)
解法二: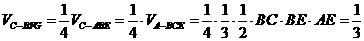 .
(12分)
.
(12分)
20、(本小题满分14分)
如图,矩形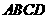 中,
中,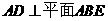 ,
,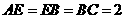 ,
,
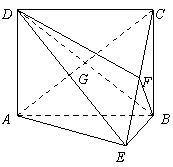
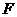 为
为 上的点,且
上的点,且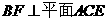 ,
,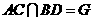 .
.
(Ⅰ)求证: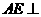 平面
平面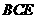 ;
;
(Ⅱ)求证: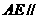 平面
平面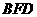 ;
;
(Ⅲ)求三棱锥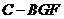 的体积.
的体积.
19.(本小题满分12分)
解:(1)记事件A为“任取两张卡片,将卡片上的函数相加得到的函数是奇函数”,由题意知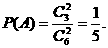 …………………………………………………4分
…………………………………………………4分
(2)ξ可取1,2,3,4.
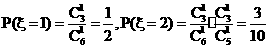 ,
,
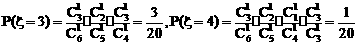 ; ………8分
; ………8分
故ξ的分布列为
|
ξ |
1 |
2 |
3 |
4 |
|
P |
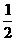 |
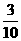 |
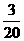 |
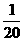 |
………………………………………………10分
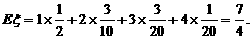
答:ξ的数学期望为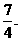 ………………………………………………12分
………………………………………………12分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com