
题目列表(包括答案和解析)
5.设x>0,y>0且x≠y,求证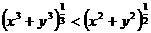
证明:由x>0,y>0且x≠y,要证明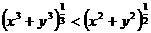
只需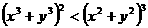 即
即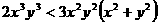
只需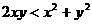
由条件,显然成立.∴原不等式成立
考点3 基本不等式在实际中的应用
题型1.处理恒成立的有关问题
例1. (2008·中山)若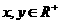 ,且
,且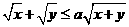 恒成立,则
恒成立,则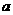 的最小值是________
的最小值是________
[解题思路]分离系数得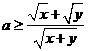 令
令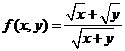 求最大值即可
求最大值即可
解析: 事实上求函数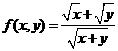 的最大值,即
的最大值,即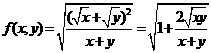 的最大值,运用基本不等式不难得到
的最大值,运用基本不等式不难得到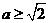 .
.
[名师指引]分离系数法是处理参数取值范围的常用方法.
题型2.处理函数应用题
.例2.(2008·梅县)某厂生产某种产品的年固定成本为250万元,每生产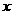 千件,需另投入成本为
千件,需另投入成本为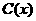 .当年产量不足80千件时,
.当年产量不足80千件时,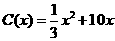 (万元);当年产量不小于80千件时,
(万元);当年产量不小于80千件时,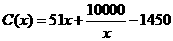 (万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(万元).每件商品售价为0.05万元.通过市场分析,该厂生产的商品能全部售完.
(1)写出年利润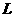 (万元)关于年产量
(万元)关于年产量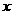 (千件)的函数解析式;
(千件)的函数解析式;
(2)年产量为多少千件时,该厂在这一商品的生产中所获利润最大?
[解题思路]凑出基本不等式的形式.
解析: (1)当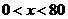 时,
时,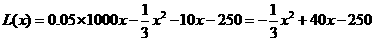
当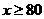 时,
时,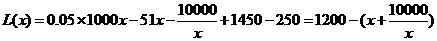
∴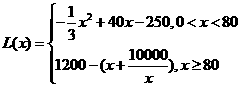
(2)当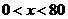 时,
时,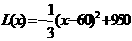 ,此时,当
,此时,当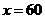 时,
时,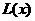 取得最大值
取得最大值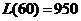 (万元);
(万元);
当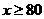 时,
时,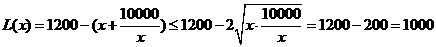
此时,当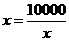 时,即
时,即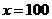 时,
时,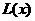 取得最大值1000万元.
取得最大值1000万元.
所以,当产量为100千件时,该厂在这一商品中所获利润最大,最大利润为1000万元.
[名师指引]形如函数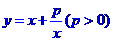 的形式求最值时可考虑用基本不等式,但要注意条件的限制,可借助函数的图像解题,必要时借助于导数.
的形式求最值时可考虑用基本不等式,但要注意条件的限制,可借助函数的图像解题,必要时借助于导数.
题型3.处理数列应用题
例3. 某乡为提高当地群众的生活水平,由政府投资兴建了甲、乙两个企业,2007年该乡从甲企业获得利润320万元,从乙企业获得利润720万元.以后每年上交的利润是:甲企业以1.5倍的速度递增,而乙企业则为上一年利润的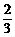 .根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
.根据测算,该乡从两个企业获得的利润达到2000万元可以解决温饱问题,达到8100万元可以达到小康水平.
(1)若以2007年为第一年,则该乡从上述两个企业获得利润最少的一年是那一年,该年还需要筹集多少万元才能解决温饱问题?
(2)试估算2015年底该乡能否达到小康水平?为什么?
[解题思路]经审题抽象出数列模型
[解析](Ⅰ)若以2007年为第一年,则第n年该乡从这两家企业获得的利润为
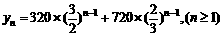 =
=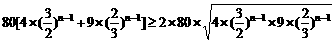 =
=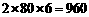
当且仅当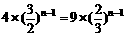 ,即n=2时,等号成立,
,即n=2时,等号成立,
所以第二年(2008年)上交利润最少,利润为960万元.
由2000–960=1040(万元)知:还需另筹资金1040万元可解决温饱问题.
(Ⅱ)2015年为第9年,该年可从两个企业获得利润
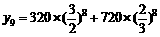
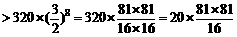
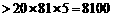
所以该乡到2015年底可以达到小康水平.
[名师指引]本题重点考查数列的相关知识,基本不等式起到了工具性的作用.
[新题导练]
4.已知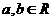 ,求证:
,求证: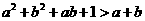
解析:∵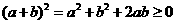 ∴
∴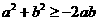 ① 又∵
① 又∵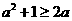 ②
② 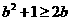 ③
③
由①②③得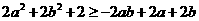 ∴
∴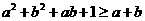 ,又不等式①、②、③中等号成立的条件分别为
,又不等式①、②、③中等号成立的条件分别为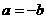 ,
,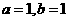 ,故不能同时成立,从而
,故不能同时成立,从而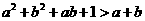 .
.
3. 已知一动直线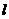 与两坐标轴的正半轴围成的三角形的面积的数值比直线
与两坐标轴的正半轴围成的三角形的面积的数值比直线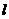 的纵、横截距之和大1,求这三角形面积的最小值.
的纵、横截距之和大1,求这三角形面积的最小值.
解析: 设直线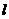 的方程
的方程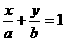 (a>0,b>0),则
(a>0,b>0),则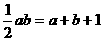 ,∵a+b>2
,∵a+b>2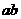 ,
,
∴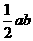 ≥
≥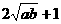 ,即
,即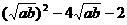 ≥0,解得
≥0,解得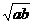 ≥
≥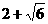 ,
,
∴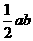 ≥
≥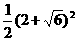 ,当a=b=2+
,当a=b=2+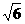 时,三角形面积的最小值为5+2
时,三角形面积的最小值为5+2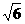
考点2 利用基本不等式证明
题型:用综合法证明简单的不等式
例1.
已知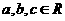 ,求证:
,求证: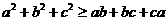 .
.
[解题思路]因为是轮换对称不等式,可考虑由局部证整体.
[解析] 
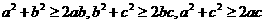 ,
,
相加整理得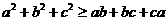 .
.
当且仅当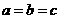 时等号成立.
时等号成立.
[名师指引]综合法证明不等式常用两个正数的算术平均数不小于它们的几何平均数这一结论,运用时要结合题目条件,有时要适当变形.
例2. 已知a,b为正数,求证: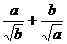 ≥
≥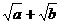 .
.
[解题思路]观察结构用基本不等式加以证明.
解析1:∵ a>0,b>0,
∴
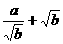 ≥
≥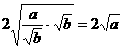 ,
,
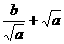 ≥
≥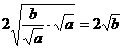 ,
,
两式相加,得
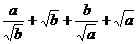 ≥
≥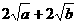 ,
,
∴
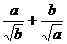 ≥
≥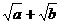 .
.
解析2. 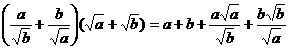 ≥
≥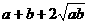
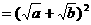 .
.
∴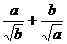 ≥
≥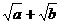 .
.
解析3.∵ a>0,b>0,∴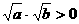 ,
,
∴
欲证 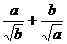 ≥
≥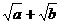 ,
,
即证 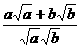 ≥
≥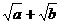 ,
,
只要证 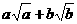 ≥
≥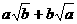 ,
,
只要证 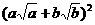 ≥
≥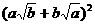 ,
,
即证 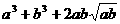 ≥
≥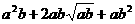 ,
,
只要证 a3+b3≥ab(a+b),
只要证 a2+b2-ab≥ab,
即证 (a-b)2≥0.
∵ (a-b)2≥0成立,∴ 原不等式成立 .
[名师指引]当要证明的不等式形式上比较复杂时,常通过分析法寻求证题思路.
“分析法”与“综合法”是数学推理中常用的思维方法,特别是这两种方法的综合运用能力,对解决实际问题有重要的作用. 这两种数学方法是高考考查的重要数学思维方法.
[新题导练]
2. .(2008·华附)已知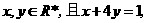 则
则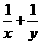 的最小值为
的最小值为
解析:∵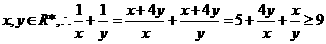 ,当且仅当
,当且仅当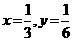 时取等号.
时取等号.
1.若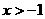 ,则
,则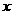 =_____时,
=_____时,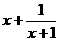 有最小值,最小值为_____.
有最小值,最小值为_____.
解析:∵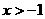 , ∴
, ∴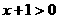 , ∴
, ∴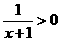 ,∴
,∴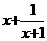 =
=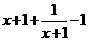
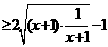
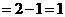 ,当且仅当
,当且仅当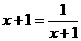 即
即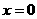 时
时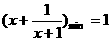 .
.
7.已知二次函数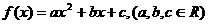 满足:对任意实数x,都有
满足:对任意实数x,都有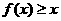 ,且当
,且当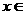 (1,3)时,有
(1,3)时,有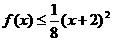 成立。
成立。
(1)证明: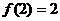 ;
;
(2)若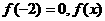 的表达式;
的表达式;
(3)设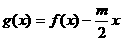 ,
,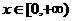 ,若
,若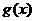 图上的点都位于直线
图上的点都位于直线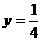 的上方,求
的上方,求
实数m的取值范围。
解析:(1)由条件知 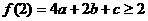 恒成立
恒成立
又∵取x=2时,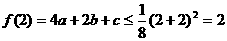 与恒成立,
与恒成立,
∴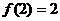 .
.
(2)∵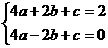 ∴
∴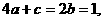 ∴
∴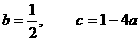 .
.
又 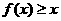 恒成立,即
恒成立,即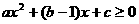 恒成立.
恒成立.
∴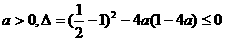 ,
,
解出: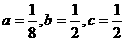 ,
,
∴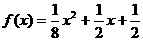 .
.
(3)由分析条件知道,只要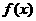 图象(在y轴右侧)总在直线
图象(在y轴右侧)总在直线 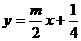 上方即可,也就是直线的斜率
上方即可,也就是直线的斜率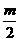 小于直线与抛物线相切时的斜率位置,于是:
小于直线与抛物线相切时的斜率位置,于是:
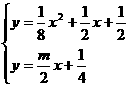
∴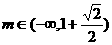 .
.
解法2: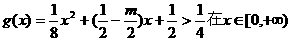 必须恒成立,
必须恒成立,
即 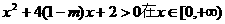 恒成立.
恒成立.
①△<0,即 [4(1-m)]2-8<0,解得: ;
;
②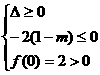 解出:
解出: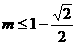 .
.
总之,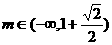 .
.
|

|
版权所有:()
版权所有:()
6.(广东省深圳外国语学校2008届第三次质检)据调查,某地区100万从事传统农业的农民,人均收入3000元,为了增加农民的收入,当地政府积极引进资本,建立各种加工企业,对当地的农产品进行深加工,同时吸收当地部分农民进入加工企业工作,据估计,如果有x(x>0)万人进企业工作,那么剩下从事传统农业的农民的人均收入有望提高2x%,而进入企业工作的农民的人均收入为3000a元(a>0)。
(I)在建立加工企业后,要使从事传统农业的农民的年总收入不低于加工企业建立前的农民的年总收入,试求x的取值范围;
(II)在(I)的条件下,当地政府应该如何引导农民(即x多大时),能使这100万农民的人均年收入达到最大。
解:(I)由题意得(100-x)·3000·(1+2x%)≥100×3000,
即x2-50x≤0,解得0≤x≤50,
又∵x>0 ∴0<x≤50;
(II)设这100万农民的人均年收入为y元,
则y= =
=-[x-25(a+1)]2+3000+475(a+1)2 (0<x≤50)
(i)当0<25(a+1)≤50,即0<a≤1,当x=25(a+1)时,y最大;
(ii)当25(a+1)>50,即a >1,函数y在(0,50]单调递增,∴当x=50时,y取最大值
答:在0<a≤1时,安排25(a +1)万人进入企业工作,在a>1时安排50万人进入企业工作,才能使这100万人的人均年收入最大
6.. 已知a>0,且a≠1,解关于x的不等式:
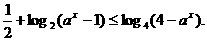
解:原不等式等价于
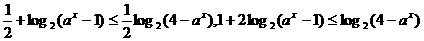
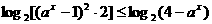
原不等式同解于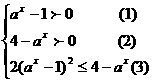 7分
7分
由①②得1<ax<4,
由③得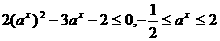
从而1<ax≤2 10分
①当a>1时,原不等式解为{x|0<x≤loga2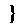
②当0<a<1时,原不等式解为{x|loga2≤x<0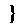
5.解关于x的不等式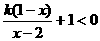 (k≥0,k≠1).
(k≥0,k≠1).
原不等式即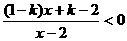 ,
,
1°若k=0,原不等式的解集为空集;
2°若1-k>0,即0<k<1时,原不等式等价于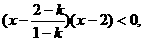
此时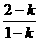 -2=
-2=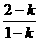 >0,
>0,
∴若0<k<1,由原不等式的解集为{x|2<x<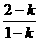 };
};
3°若1-k<0,即k>1时,原不等式等价于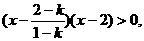
此时恒有2>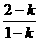 ,所以原不等式的解集为{x|x<
,所以原不等式的解集为{x|x<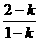 ,或x>2}.
,或x>2}.
综合拔高训练
3. (广东省五校2008年高三上期末联考) 若关于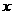 的不等式
的不等式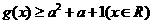 的解集为空集,则实数
的解集为空集,则实数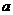 的取值范围是
.
的取值范围是
.
解析: 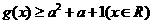 的解集为空集,就是1= [
的解集为空集,就是1= [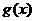 ]max<
]max<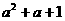
所以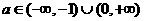
4(08梅州)设命题P:函数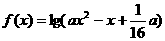 的定义域为R;命题q:不等式
的定义域为R;命题q:不等式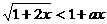 对一切正实数均成立。如果命题p或q为真命题,命题p且q为假命题,求实数
对一切正实数均成立。如果命题p或q为真命题,命题p且q为假命题,求实数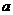 的取值范围。
的取值范围。
解:命题P为真命题 函数
函数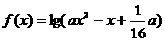 定义域为R
定义域为R
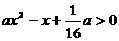 对任意实数
对任意实数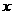 均成立
均成立
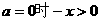 解集为R,或
解集为R,或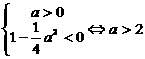 ∴ 命题P为真命题
∴ 命题P为真命题
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com