
题目列表(包括答案和解析)
17.(本小题满分12分)
在△ABC中,已知角A、B、C所对的边分别为a、b、c,直线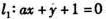 与
与
直线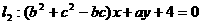 互相平行(其中a ≠4)
互相平行(其中a ≠4)
(I)求角A的值,
(II)若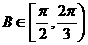 B,求
B,求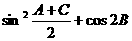 的取值范围
的取值范围
22.(本题满分14分)设函数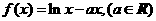
(Ⅰ)判断函数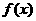 的单调性;
的单调性;
(Ⅱ)当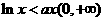 上恒成立时,求
上恒成立时,求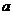 的取值范围;
的取值范围;
(Ⅲ)证明: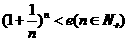
解: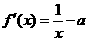 …………………………………………………………………………2分
…………………………………………………………………………2分
(Ⅰ) 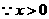 所以当
所以当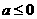 时,
时,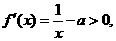
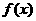 在
在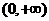 是增函数 …………………………………………………………………4分
是增函数 …………………………………………………………………4分
当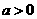 时,
时,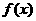 在
在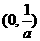 上
上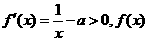 在
在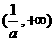 上
上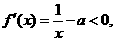
故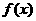 在
在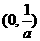 上是增函数,
上是增函数,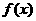 在
在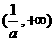 上是减函数……………………………6分
上是减函数……………………………6分
(Ⅱ)由(Ⅰ)知当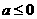 时,
时,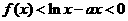 在
在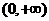 上不恒成立;……………8分
上不恒成立;……………8分
当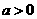 时,
时,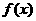 在
在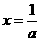 处取得最大值为
处取得最大值为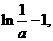 因此
因此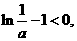 即
即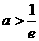 时,
时,
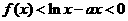 在
在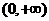 上恒成立,即
上恒成立,即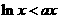 在
在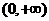 上恒成立。
上恒成立。
所以当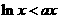 在
在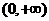 上恒成立时,
上恒成立时,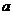 的取值范围为
的取值范围为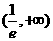 ……………………10分
……………………10分
(Ⅲ)由(Ⅱ)知当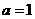 时,
时,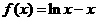 的最大值为
的最大值为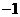
所以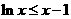 (当且仅当
(当且仅当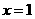 时等号成立),令
时等号成立),令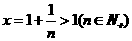 ,则得
,则得
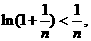 即
即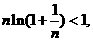 …………………………………………………………12分
…………………………………………………………12分
从而得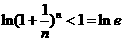
由函数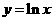 的单调性得
的单调性得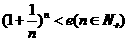 ………………………………………14分
………………………………………14分
[2010淄博一模]
21.(本题满分12分)已知曲线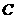 上任意一点
上任意一点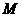 到点
到点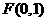 的距离比它到直线
的距离比它到直线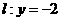 的距离小
的距离小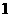 。
。
(Ⅰ)求曲线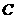 的方程;
的方程;
(Ⅱ)过点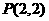 的直线
的直线 与曲线
与曲线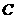 交于
交于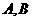 两点,设
两点,设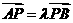
①当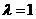 时,求直线
时,求直线 的方程;
的方程;
②当 的面积为
的面积为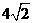 时(
时( 为坐标原点),求直线
为坐标原点),求直线 的斜率。
的斜率。
解:(Ⅰ) 点
点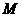 到
到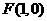 的距离比它到直线
的距离比它到直线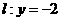 的距离小于
的距离小于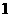
 点
点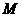 在直线
在直线 的上方,
的上方,
点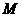 到
到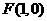 的距离与它到直线
的距离与它到直线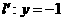 的距离相等
的距离相等
 点
点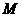 的轨迹
的轨迹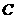 是以
是以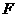 为焦点,
为焦点,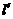 为准线的抛物线
为准线的抛物线
所以曲线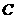 的方程为
的方程为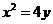 ……………………………………………………………4分
……………………………………………………………4分
(Ⅱ))当直线 的斜率不存在时,它与曲线
的斜率不存在时,它与曲线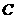 只有一个交点,不合题意,
只有一个交点,不合题意,
设直线 的方程为
的方程为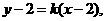 即
即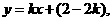
带入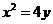 得
得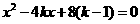
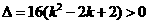 对
对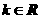 恒成立,所以直线
恒成立,所以直线 与曲线
与曲线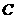 恒有两个不同的交点
恒有两个不同的交点
设交点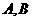 的坐标分别为
的坐标分别为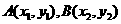
则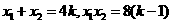 ……………………………………………………………6分
……………………………………………………………6分
①由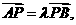 且
且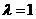 得点
得点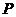 是弦
是弦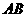 的中点,
的中点,
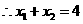 ,则
,则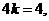 得
得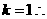 直线
直线 的方程是
的方程是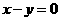 ………………………8分
………………………8分
②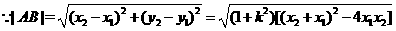
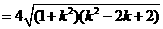
点 到直线
到直线 的距离
的距离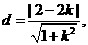 ……………………………………………………10分
……………………………………………………10分
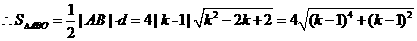
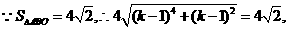
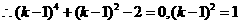 或
或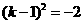 (舍去)
(舍去)
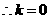 或
或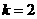 ……………………………………………………………………………12分
……………………………………………………………………………12分
20.(本题满分12分)已知当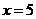 时,二次函数
时,二次函数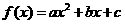 取得最小值,等差数列
取得最小值,等差数列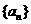 的前
的前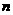 项和
项和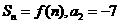
(Ⅰ)求数列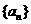 的通项公式;
的通项公式;
(Ⅱ)令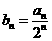 ,数列
,数列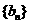 的前
的前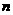 项和为
项和为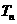 ,证明
,证明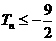 。
。
解:(Ⅰ)由题意得: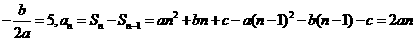
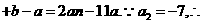 得
得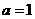 ………………………………………………4分
………………………………………………4分
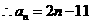 ………………………………………………………………………………6分
………………………………………………………………………………6分
(Ⅱ) 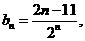
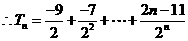 ①
①
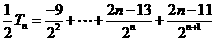 ②
②
①-②得
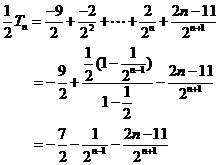
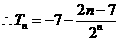 ………………………………………………………………………10分
………………………………………………………………………10分
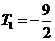
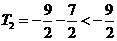
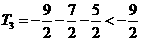
当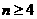 时,
时,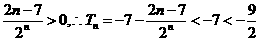
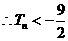 …………………………………………………………………………………12分
…………………………………………………………………………………12分
19.(本地满分12分)某足球俱乐部和其他4支俱乐部进行足球联赛,它要与其他每支球队各赛一场,在4场的任意一场中,此俱乐部每次胜、负、平的概率相等。已知当这四场比赛结束后,该俱乐部胜场多于负场。
(Ⅰ)求该俱乐部胜场多于负场的所有可能的个数和;
(Ⅱ)若胜场次数为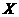 ,求出
,求出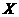 的分布列并求
的分布列并求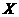 的数学期望。
的数学期望。
解:(Ⅰ)若胜一场,则其余为平,共有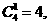 ………………………………………2分
………………………………………2分
若胜两场,则其余两场有一负一平和两平两种情况,
共有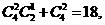 ………………………………………………………………………4分
………………………………………………………………………4分
若胜三场,则其余一场有负和平两种情况,
共有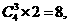 ……………………………………………………………………………6分
……………………………………………………………………………6分
若胜四场,则只有一种情况,共有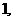
综上,共有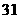 种情况。……………………………………………………………………8分
种情况。……………………………………………………………………8分
(Ⅱ)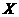 可能取值为
可能取值为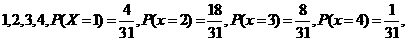
所以分布列为。
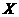
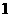
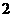
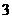
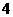
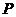
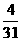
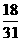
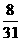
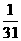
………………………………10分
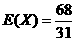 …………………………………………………………………………………12分
…………………………………………………………………………………12分
18. (本题满分12分)如图,在五面体
(本题满分12分)如图,在五面体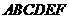 中,
中,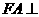
平面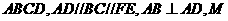 为
为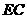 的中
的中
点,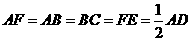 。
。
(Ⅰ)求异面直线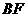 与
与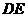 所成的角的大小;
所成的角的大小;
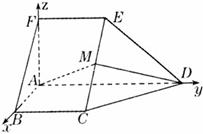 (Ⅱ)证明:平面
(Ⅱ)证明:平面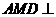 平面
平面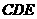 ;
;
(Ⅲ)求二面角 的余弦值。
的余弦值。
解:如图建立空间直角坐标系,设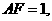 则
则
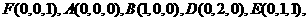
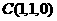
因为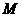 为
为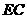 的中点,则
的中点,则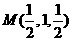
(Ⅰ) 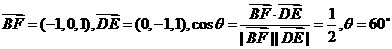 ………………4分
………………4分
(Ⅱ) 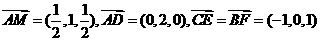 ,则
,则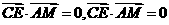
所以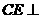 平面
平面 ,得平面
,得平面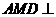 平面
平面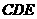 ; ………………………………8分
; ………………………………8分
(Ⅲ)由图可得平面 的法向量为
的法向量为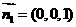 ,设平面
,设平面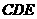 的法向量为
的法向量为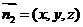
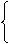
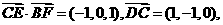 列方程组的
列方程组的 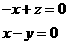 得
得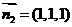
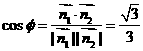 ……………………………………………………………………12分
……………………………………………………………………12分
17.(本题满分12分)在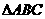 中,角
中,角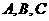 所列边分别为
所列边分别为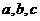 ,且
,且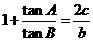 。
。
(Ⅰ)求角 ;
;
(Ⅱ)若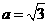 ,试判断
,试判断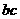 取得最大值时
取得最大值时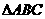 形状。
形状。
解:(Ⅰ) 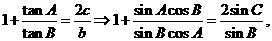 ………………………………2分
………………………………2分
即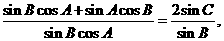
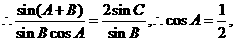 ………………………………………………4分
………………………………………………4分
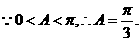 ……………………………………………………………………6分
……………………………………………………………………6分
(Ⅱ)在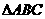 中,
中,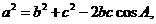 且
且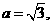
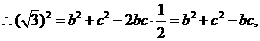
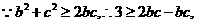
即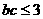 ,当且仅当
,当且仅当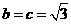 时,
时,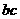 取得最大值, ………………………………9分
取得最大值, ………………………………9分
又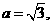
故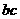 取得最大值时,
取得最大值时,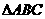 为等边三角形 ……………………………………………12分
为等边三角形 ……………………………………………12分
22.(本题满分14分)设函数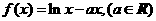
(Ⅰ)判断函数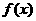 的单调性;
的单调性;
(Ⅱ)当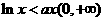 上恒成立时,求
上恒成立时,求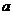 的取值范围;
的取值范围;
(Ⅲ)证明: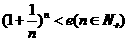
[2010德州一模]答案
21.(本题满分12分)已知曲线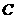 上任意一点
上任意一点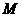 到点
到点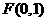 的距离比它到直线
的距离比它到直线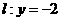 的距离小
的距离小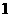 。
。
(Ⅰ)求曲线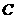 的方程;
的方程;
(Ⅱ)过点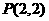 的直线
的直线 与曲线
与曲线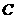 交于
交于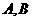 两点,设
两点,设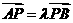
①当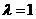 时,求直线
时,求直线 的方程;
的方程;
②当 的面积为
的面积为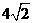 时(
时( 为坐标原点),求直线
为坐标原点),求直线 的斜率。
的斜率。
20.(本题满分12分)已知当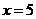 时,二次函数
时,二次函数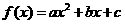 取得最小值,等差数列
取得最小值,等差数列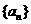 的前
的前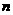 项和
项和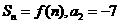
(Ⅰ)求数列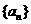 的通项公式;
的通项公式;
(Ⅱ)令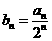 ,数列
,数列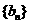 的前
的前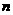 项和为
项和为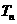 ,证明
,证明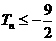 。
。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com