
题目列表(包括答案和解析)
21.解:
(1)设椭圆的方程为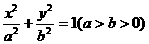 ,则
,则
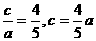 ,
,

 椭圆过点
椭圆过点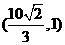
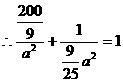 ,
,
解处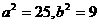
故椭圆C的方程为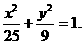 6分
6分
(2)设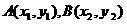 分别为直线
分别为直线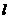 与椭圆和圆的切点,
与椭圆和圆的切点,
直线AB的方程为: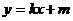
因为A既在椭圆上,又在直线AB上,
从而有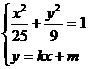 ,
,
消去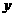 得:
得: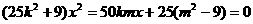
由于直线与椭圆相切,
故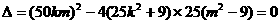
从而可得: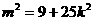 ①
①
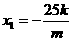 ②
②
由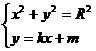
消去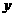 得:
得: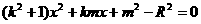
由于直线与圆相切,得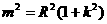 ③
③
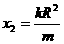 ④
④
由①③得: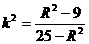
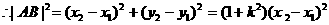
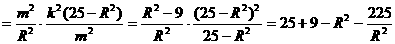
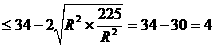
即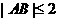 ,当且仅当
,当且仅当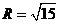 时取等号,所以|AB|的最大值为2。 13分
时取等号,所以|AB|的最大值为2。 13分
(20)(本小题满分12分)
函数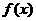 对任意
对任意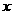 ∈R都有
∈R都有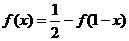
(I)求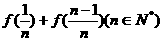 的值;
的值;
(II) 数列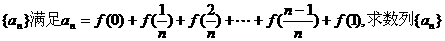 的通项公式.
的通项公式.
(III)令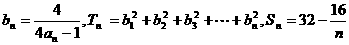 试比较Tn与Sn的大小.
试比较Tn与Sn的大小.
21.(本小题满分13分)
已知焦点在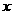 轴上,中心在坐标原点的椭圆C的离心率为
轴上,中心在坐标原点的椭圆C的离心率为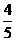 ,且过点
,且过点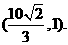
(1)求椭圆C的方程;
(2)直线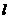 分别切椭圆C与圆
分别切椭圆C与圆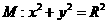 (其中
(其中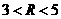 )于A、B两点,求|AB|的最大值。
)于A、B两点,求|AB|的最大值。
20.解:
(1)由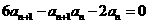
得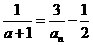 ,
,
则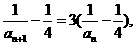
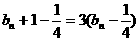
所以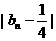 是以3为公比,
是以3为公比,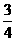 为首项的等比数列
为首项的等比数列
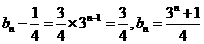 6分
6分
(2)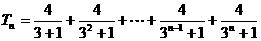
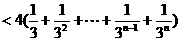
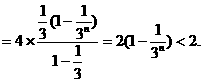 13分
13分
20.(本小题满分13分)
各项均不为零的数列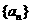 ,首项
,首项 ,且对于任意
,且对于任意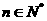 均有
均有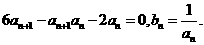
(1)求数列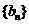 的通项公式;
的通项公式;
(2)数列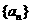 的前
的前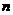 项和为
项和为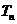
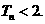
19.解:
设B型号电视机的价值为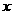 万元(
万元(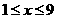 ),农民得到的补贴为
),农民得到的补贴为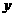 万元,
万元,
则A型号电视机的价值为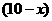 万元,
万元,
由题意得,
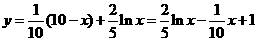 6分
6分
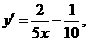
由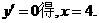
当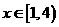 时,
时,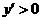 ,
,
当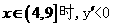
所以当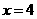 时,
时,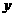 取最大值,
取最大值,
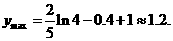
即厂家分别投放A、B两型号电视机6万元和4万元时,农民得到补贴最我,最多补贴约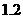 万元。
13分
万元。
13分
19.(本小题满分13分)
某电视生产厂家有A、B两种型号的电视机参加家电下乡活动。若厂家投放A、B型号电视机的价值分别为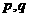 万元,农民购买电视机获得的补贴分别为
万元,农民购买电视机获得的补贴分别为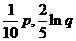 万元。已知厂家把总价值为10万元的A、B两种型号电视机投放市场,且A、B两型号的电视机投放金额都不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值(精确到
万元。已知厂家把总价值为10万元的A、B两种型号电视机投放市场,且A、B两型号的电视机投放金额都不低于1万元,请你制定一个投放方案,使得在这次活动中农民得到的补贴最多,并求出其最大值(精确到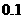 ,参考数据:
,参考数据: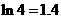 )
)
21.(1)证明:∵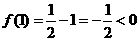 ,
,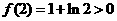
∴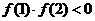 且函数
且函数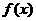 在(1,2)上连续,
在(1,2)上连续,
∴函数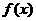 在(1,2)上有零点,即
在(1,2)上有零点,即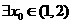 ,使得
,使得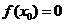 -------4分
-------4分
(2)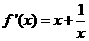 --------------------------------------------------5分
--------------------------------------------------5分
当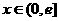 时,
时,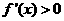
∴函数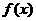 在
在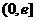 上为增函数--------------------------------------7分
上为增函数--------------------------------------7分
∴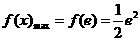
不等式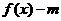 ≤0,对
≤0,对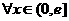 恒成立等价于
恒成立等价于 ≥
≥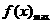 ,
,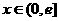
∴ ≥
≥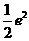 -----------------------------------------------------------9分
-----------------------------------------------------------9分
(3)证明:令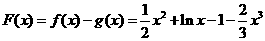 -------------------10分
-------------------10分
则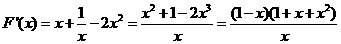 ---------------12分
---------------12分
∵当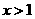 时
时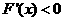 ,∴函数
,∴函数 在区间
在区间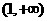 上为减函数
上为减函数
∴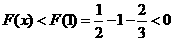
即在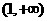 上,
上,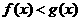
∴在区间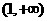 上,函数
上,函数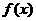 的图象在函数
的图象在函数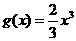 的图象的下方------14分
的图象的下方------14分
21.(本小题满分14分)
已知函数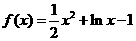 .
.
(1)试证明: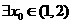 ,使得
,使得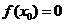
(2)已知不等式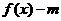 ≤0,对
≤0,对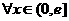 (
(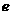 =2.718…)恒成立,求实数
=2.718…)恒成立,求实数 的取值范围;
的取值范围;
(3)求证:在区间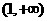 上,函数
上,函数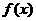 的图象在函数
的图象在函数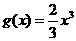 的图象的下方.
的图象的下方.
20.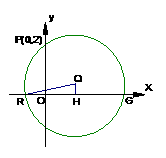 解:(1)设圆心
解:(1)设圆心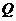 的坐标为
的坐标为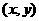 ,如图过圆心
,如图过圆心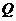 作
作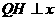 轴于H,
轴于H,
则H为RG的中点,在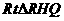 中,
中,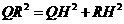 -------2分
-------2分
∵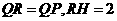
∴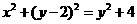
即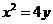 ----------------------------------------------------------6分
----------------------------------------------------------6分
(2) 设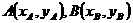 ,
,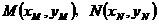
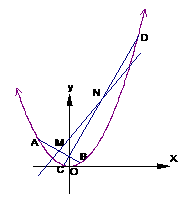 直线AB的方程为
直线AB的方程为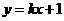 则
则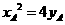 -------------①
-------------①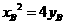 ----------②
----------②
由①-②得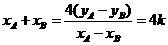 ,∴
,∴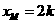 ,
,
∵点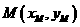 在直线
在直线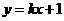 上, ∴
上, ∴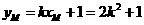 .
.
∴点M的坐标为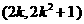 .---------------------------------------------10分
.---------------------------------------------10分
同理可得: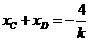 ,
, 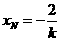 ,
,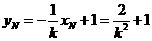
∴点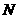 的坐标为
的坐标为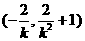 . ------------------------------------------12分
. ------------------------------------------12分
直线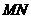 的斜率为
的斜率为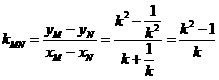 ,其方程为
,其方程为
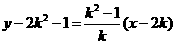 ,整理得
,整理得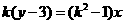 ,
,
显然,不论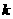 为何值,点
为何值,点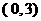 均满足方程,
均满足方程,
∴直线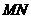 恒过定点
恒过定点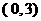 .----------------------------------14分
.----------------------------------14分
20.(本小题满分14分)
设圆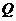 过点P(0,2), 且在
过点P(0,2), 且在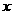 轴上截得的弦RG的长为4.
轴上截得的弦RG的长为4.
(1)求圆心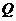 的轨迹E的方程;
的轨迹E的方程;
(2)过点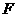 (0,1),作轨迹
(0,1),作轨迹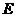 的两条互相垂直的弦
的两条互相垂直的弦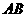 、
、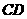 ,设
,设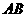 、
、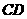 的中点分别为
的中点分别为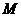 、
、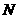 ,试判断直线
,试判断直线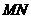 是否过定点?并说明理由.
是否过定点?并说明理由.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com