
题目列表(包括答案和解析)
5. 设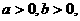 求证
求证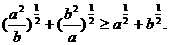
证法一:左边-右边=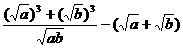
=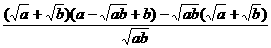
= 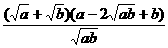 =
=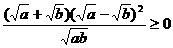 ∴原不等式成立。
∴原不等式成立。
证法二:左边>0,右边>0。
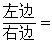
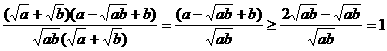 ∴原不等式成立。
∴原不等式成立。
综合拔高训练
4.若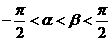 ,则
,则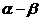 的取值范围是
的取值范围是
解析:由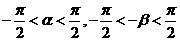 ,
,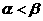 可得
可得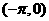
3. 若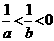 ,则下列不等式:①
,则下列不等式:①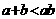 ;②
;②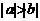 ;③
;③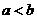 ;④
;④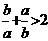 中,正确的不等式有( )
中,正确的不等式有( )
A.1个 B.2个 C.3个 D.4个
解析:由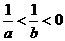 得
得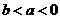 ,
,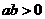 ,则①④正确,②③错误,故选B.
,则①④正确,②③错误,故选B.
2.(2008·吴川一中)对于实数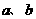 ,“
,“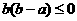 ”是“
”是“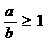 ”成立的( )
”成立的( )
A.充分不必要条件 B.必要不充分条件
C.充要条件 D.既不充分又不必要条件
解析:由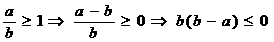 ;反之不成立.选 C
;反之不成立.选 C
1.
如果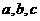 满足
满足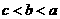 ,且
,且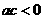 ,那么下列选项中不一定成立的是( )
,那么下列选项中不一定成立的是( )
A.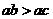 B.
B.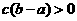 C.
C.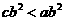 D.
D. 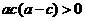
解析:由题意知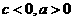 ,则
,则 一定正确,B一定正确,D一定正确,故选C(当b=0时)
一定正确,B一定正确,D一定正确,故选C(当b=0时)
6. 已知等差数列{an}的公差大于0,且a3,a5是方程x2-14x+45=0的两根,数列{bn}的前n项和为Sn,且Sn=1- bn. (1)求数列{an}、{bn]的通项公式; (2)记cn=anbn,求证:cn+1≤cn. 解:(1)因为a3,a5是方程x2-14x+45=0的两根,且数列{an}的公差d>0, ∴a3=5,a5=9,从而d==2 ∴an=a5+(n-5)d=2n-1 又当n=1时,有b1=S1=1- b1,∴b1= 当n≥2时,有bn=Sn-Sn-1=(bn-1-bn) ∴(n≥2) ∴数列{bn}是等比数列,且b1=,q= ∴bn=b1qn-1=; (2)由(1)知:cn=anbn=,cn+1=
∴cn+1-cn=≤0 ∴cn+1≤cn.
★ 抢 分 频 道 ★
基础巩固训练
5. 已知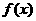 是定义在
是定义在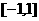 上的奇函数,且
上的奇函数,且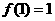 ,若
,若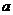 、
、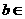
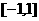 ,
,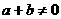 ,有
,有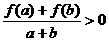 ;
;
(1)、判断函数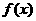 在
在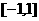 上的单调性,并证明你的结论;
上的单调性,并证明你的结论;
(2)、若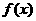 ≤
≤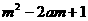 对所有的
对所有的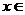
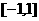 、
、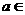
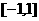 恒成立,求实数
恒成立,求实数 的取值范围。
的取值范围。
解:(1)、依题意,令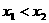 ,且
,且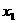 、
、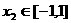 ,则
,则
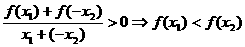 ,则函数
,则函数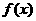 在
在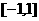 上的单调增。
上的单调增。
(2)、依题意,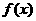 在
在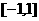 上的最大值为1,则
上的最大值为1,则 对
对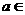
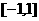 恒成立,
恒成立, 对
对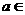
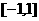 恒成立,
恒成立,
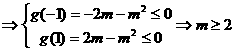 或
或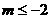 或
或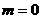 。
。
4. 已知四个条件,①b>0>a ②0>a>b ③a>0>b ④a>b>0能推出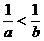 成立的有( )
成立的有( )
A.1个 B.2个 C.3个 D.4个
解析:运用倒数法则,a>b,ab>0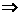
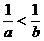 ,②、④正确.又正数大于负数,故选C.
,②、④正确.又正数大于负数,故选C.
考点3 不等式性质综合应用
题型1.用比较法证函数的单调性
例1. (广东省揭阳二中2009届高三上学期期中考试)
已知函数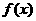 的定义域为
的定义域为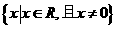 对定义域内的任意
对定义域内的任意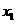 、
、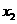 ,都有
,都有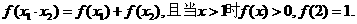
(1)求证: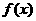 是偶函数;
是偶函数;
(2)求证: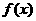 在
在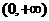 上是增函数;
上是增函数;
(3)解不等式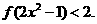
[解题思路]证明抽象函数的单调性通常是用单调性的定义结合比较法.
解析;(1)证明 因对定义域内的任意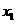 、
、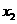 都有
都有
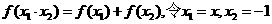 ,则有
,则有
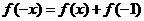 ……2分
……2分
又令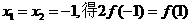
再令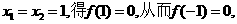
于是有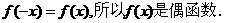
(2)设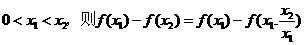
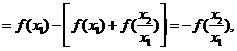
由于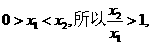 从而
从而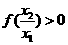 ,
,
故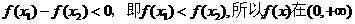 上是增函数. (3)由于
上是增函数. (3)由于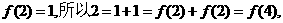
于是待解不等式可化为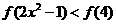 , 结合(1)(2)已证结论,可得上式等价于
, 结合(1)(2)已证结论,可得上式等价于 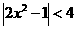
解得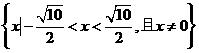 .
.
[名师指引] 作差法、作商法以及函数的单调性是比较大小的常用方法.运用不等式性质时应从结论出发, 寻找解题的切入点.
题型2.用比较法处理数列中的不等关系.
例2. (广东省揭阳市2008年高中毕业班高考调研测试改编)
已知数列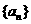 满足
满足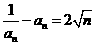 ,且
,且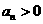 。
。
(1)求数列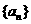 的通项公式;
的通项公式;
(2)数列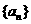 是否存在最大项?若存在最大项,求出该项和相应的项数;若不存在,说明理由。
是否存在最大项?若存在最大项,求出该项和相应的项数;若不存在,说明理由。
[解题思路]先由递推关系求通项公式,再用比较法判断数列的单调性
解:(1)由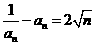 得
得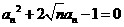 -
-
由一元二次方程求根公式得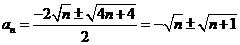

∵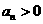 ∴
∴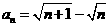
(2) 解:∵ 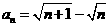 ∴
∴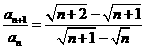
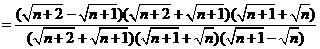
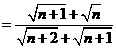
∵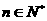 ,∴
,∴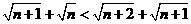 ∴
∴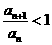 ,∵
,∵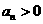
∴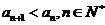 即
即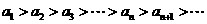
∴数列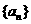 有最大项,最大项为第一项
有最大项,最大项为第一项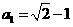 。
。
[名师指引]借助于比较法验证数列的单调性进而数列的不等关系是近年高考的热点之一.
[新题导练]
3..若a<b<0,则下列不等式不能成立的是
A.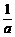 >
>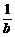 B.2a>2b
B.2a>2b
C.|a|>|b| D.(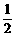 )a>(
)a>(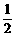 )b
)b
解析:由a<b<0知ab>0,因此a·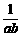 <b·
<b·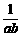 ,即
,即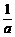 >
>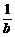 成立;
成立;
由a<b<0得-a>-b>0,因此|a|>|b|>0成立.
又(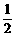 )x是减函数,所以(
)x是减函数,所以(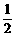 )a>(
)a>(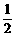 )b成立.
)b成立.
故不成立的是B.
答案:B
2. 如果一辆汽车每天行驶的路程比原来多19 km,那么在8天内它的行程就超过2 200 km,如果它每天行驶的路程比原来少12 km,那么它行驶同样的路程得花9天多的时间,这辆汽车原来每天行驶的路程(km)范围是________________.
解析:这辆汽车原来每天行驶的路程为x km,则
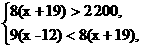 解之,得 256<x<260.答案:256<x<260
解之,得 256<x<260.答案:256<x<260
考点2 不等式的性质
题型:验证或推导简单不等式的有关结论
例1. 已知:m>n,a<b,求证:m-a>n-b.
[解题思路]以不等式的性质为基础,进行推导
证法一:由m>n知m-n>0,由a<b知b-a>0.
∴(m-a)-(n-b)=(m-n)+(b-a)>0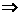 m-a>n-b;
m-a>n-b;
证法二:∵a<b ∴-a>-b
又∵m>n ∴m+(-a)>n+(-b)
∴m-a>n-b.
[名师指引]不等式的性质中,有“单向性”和“双向性”的区别,切记随心所欲、自创性质
例2.已知下列三个不等式①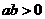 ;②
;②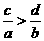 ;③
;③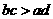 ,以其中两个作为条件,余下一个作结论,则可组成几个正确命题.
,以其中两个作为条件,余下一个作结论,则可组成几个正确命题.
[解题思路]以比较法为基础进行变形
[解析](1)对②变形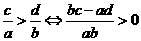 ,由
,由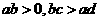 得②成立,∴①③
得②成立,∴①③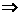 ②.
②.
(2)若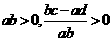 ,则
,则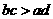 ,∴①②
,∴①②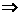 ③.(3)若
③.(3)若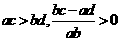 ,则
,则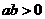 ,∴①②
,∴①②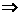 ③.
③.
综上所述可组成3个正确命题.
[名师指引]注意运用性质时须满足的条件,如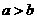 时,判断
时,判断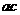 与
与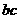 的大小关系应注意从
的大小关系应注意从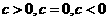 三个方面讨论.
三个方面讨论.
[新题导练].
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com