
题目列表(包括答案和解析)
20.(本小题满分16分)
设函数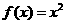 ,
,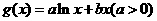 .
.
(Ⅰ)若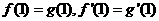 ,求
,求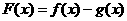 的极小值;
的极小值;
(Ⅱ)在(Ⅰ)的条件下,是否存在实常数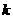 和
和 ,使得
,使得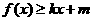 和
和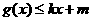 ?若存在,求出
?若存在,求出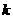 和
和 的值.若不存在,说明理由.
的值.若不存在,说明理由.
(Ⅲ)设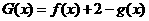 有两个零点
有两个零点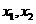 ,且
,且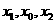 成等差数列,试探究
成等差数列,试探究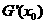 值的符号.
值的符号.




19.(本小题满分16分)
设等比数列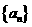 的首项为
的首项为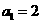 ,公比为
,公比为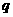 (
(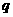 为正整数),且满足
为正整数),且满足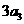 是
是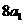 与
与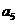 的等差中项;数列
的等差中项;数列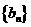 满足
满足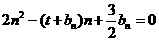 (
(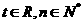 ).
).
(Ⅰ)求数列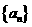 的通项公式;
的通项公式;
(Ⅱ)试确定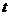 的值,使得数列
的值,使得数列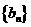 为等差数列;
为等差数列;
(Ⅲ)当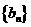 为等差数列时,对每个正整数
为等差数列时,对每个正整数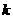 ,在
,在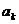 与
与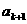 之间插入
之间插入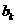 个2,得到一个新数列
个2,得到一个新数列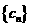 . 设
. 设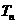 是数列
是数列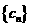 的前
的前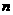 项和,试求满足
项和,试求满足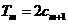 的所有正整数
的所有正整数 .
.
18.(本小题满分16分)
已知在△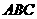 中,点
中,点 、
、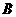 的坐标分别为
的坐标分别为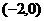 和
和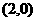 ,点
,点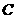 在
在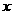 轴上方.
轴上方.
(Ⅰ)若点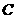 的坐标为
的坐标为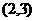 ,求以
,求以 、
、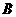 为焦点且经过点
为焦点且经过点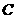 的椭圆的方程;
的椭圆的方程;
(Ⅱ)若∠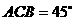 ,求△
,求△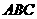 的外接圆的方程;
的外接圆的方程;
(Ⅲ)若在给定直线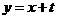 上任取一点
上任取一点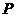 ,从点
,从点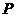 向(Ⅱ)中圆引一条切线,切点为
向(Ⅱ)中圆引一条切线,切点为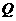 . 问是否存在一个定点
. 问是否存在一个定点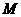 ,恒有
,恒有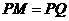 ?请说明理由.
?请说明理由.
21. [解析](1)令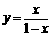 ,解得
,解得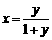 ,由
,由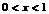 ,解得
,解得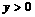 ,
,
∴函数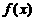 的反函数
的反函数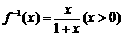 ,则
,则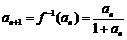 ,得
,得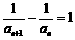 .
.
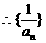 是以2为首项,l为公差的等差数列,故
是以2为首项,l为公差的等差数列,故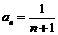 .
……3分
.
……3分
(2)∵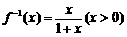 ,∴
,∴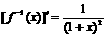 ,
,
∴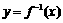 在点
在点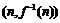 处的切线方程为
处的切线方程为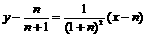 ,
,
令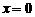 , 得
, 得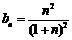 ,∴
,∴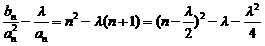 ,
,
∵仅当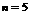 时取得最小值,∴
时取得最小值,∴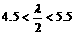 ,解之
,解之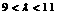 ,
,
∴的取值范围为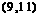 . ……7分
. ……7分
(3)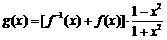
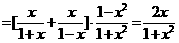 ,
,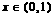 .
.
则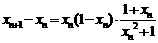 ,
,
因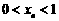 ,则
,则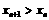 ,显然
,显然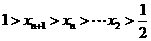 .
.
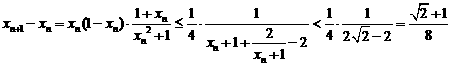
∴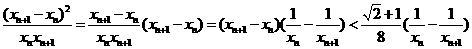
∴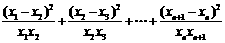
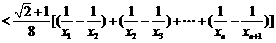
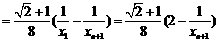
∵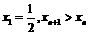 ,∴
,∴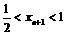 ,
,
∴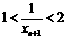 ,∴
,∴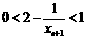
∴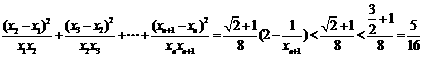 . ……12分
. ……12分
21.(本小题满分12分)已知函数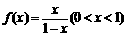 的反函数为
的反函数为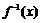 ,数列
,数列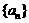 和
和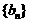 满足:
满足: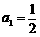 ,
,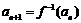 ,函数
,函数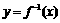 的图象在点
的图象在点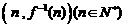 处的切线在轴上的截距为
处的切线在轴上的截距为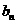 .
.
(1)求数列{ }的通项公式;
}的通项公式;
(2)若数列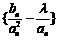 的项仅
的项仅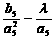 最小,求的取值范围;
最小,求的取值范围;
(3)令函数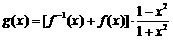 ,
,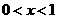 ,数列
,数列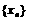 满足:
满足: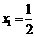 ,
,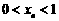 ,且
,且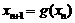 ,其中
,其中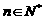 .证明:
.证明: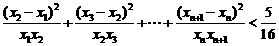 .
.
20.解:(Ⅰ)因为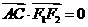 ,所以有
,所以有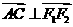
所以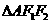 为直角三角形;
为直角三角形;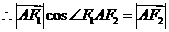 …………………………2分
…………………………2分
则有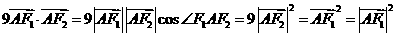
所以,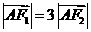 …………………………3分
…………………………3分
又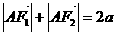 ,
,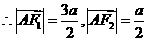 ………………………4分
………………………4分
在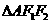 中有
中有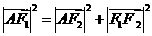
即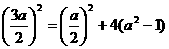 ,解得
,解得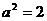
所求椭圆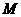 方程为
方程为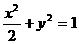 …………………………6分
…………………………6分
(Ⅱ)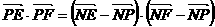
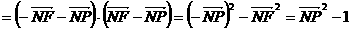
从而将求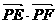 的最大值转化为求
的最大值转化为求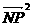 的最大值
…………………8分
的最大值
…………………8分
是椭圆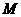 上的任一点,设
上的任一点,设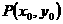 ,则有
,则有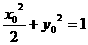 即
即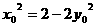
又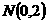 ,所以
,所以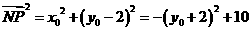 ………………10分
………………10分
而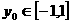 ,所以当
,所以当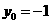 时,
时,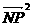 取最大值
取最大值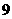
故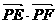 的最大值为
的最大值为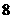 ……………………12分
……………………12分
20.(本小题满分12分)已知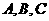 均在椭圆
均在椭圆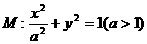 上,直线
上,直线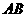 、
、 分别过椭圆的左右焦点
分别过椭圆的左右焦点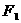 、
、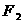 ,当
,当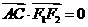 时,有
时,有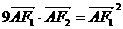 .
.
(Ⅰ)求椭圆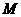 的方程;
的方程;
(Ⅱ)设是椭圆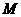 上的任一点,
上的任一点,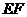 为圆
为圆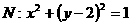 的任一条直径,求
的任一条直径,求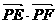 的最大值.
的最大值.
19.解:(Ⅰ)已知函数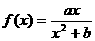 ,
,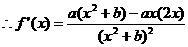 …………1分
…………1分
又函数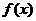 在
在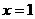 处取得极值2,
处取得极值2,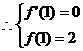 …………2分
…………2分
即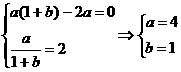
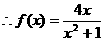 …………………4分
…………………4分
(Ⅱ)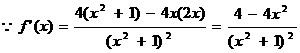 由
由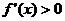 ,得
,得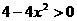 ,即
,即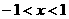
所以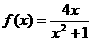 的单调增区间为(-1,1) ………………… 6分
的单调增区间为(-1,1) ………………… 6分
因函数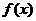 在(m,2m+1)上单调递增,
在(m,2m+1)上单调递增,
则有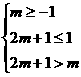 , …………7分
, …………7分
解得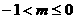 即
即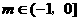 时,函数
时,函数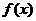 在(m,2m+1)上为增函数 ………8分
在(m,2m+1)上为增函数 ………8分
(Ⅲ)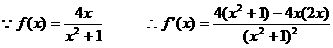
直线l的斜率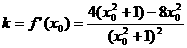 …………9分
…………9分
即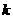
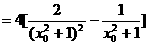 令
令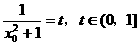 , …………10分
, …………10分
则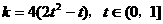
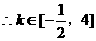 即直线l的斜率k的取值范围是
即直线l的斜率k的取值范围是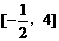 ……………12分
……………12分
19.(本小题满分12分)已知函数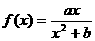 ,在
,在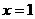 处取得极值为.
处取得极值为.
(Ⅰ)求函数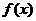 的解析式;
的解析式;
(Ⅱ)若函数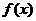 在区间
在区间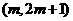 上为增函数,求实数的取值范围;
上为增函数,求实数的取值范围;
(Ⅲ)若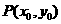 为
为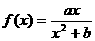 图象上的任意一点,直线
图象上的任意一点,直线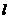 与
与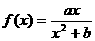 的图象相切于点,求直线
的图象相切于点,求直线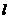 的斜率的取值范围.
的斜率的取值范围.
20.(本小题满分14分)
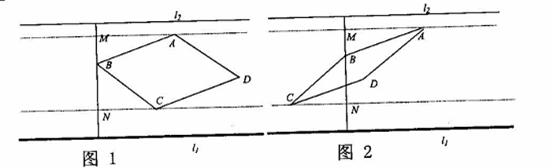
如图,在距离为600m的两条平行直道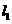 、
、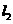 之间的B处有一重点文化古迹,该古迹到直道
之间的B处有一重点文化古迹,该古迹到直道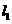 的距离是其到直道
的距离是其到直道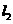 的距离地两倍。为丰富当地居民的文化生活和开发当地的旅游资源,准备在两直道间修建一个恰好以B为其中的一个顶点、形状呈菱形的公园ABCD。为安全起见,要求直道
的距离地两倍。为丰富当地居民的文化生活和开发当地的旅游资源,准备在两直道间修建一个恰好以B为其中的一个顶点、形状呈菱形的公园ABCD。为安全起见,要求直道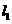 与公园最近点C的距离为100m,直到
与公园最近点C的距离为100m,直到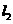 与公园最近点A的距离为50m,设直道
与公园最近点A的距离为50m,设直道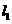 与BC所在直线的夹角为
与BC所在直线的夹角为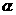 ,直道
,直道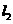 与边
与边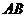 所在直线的夹角为
所在直线的夹角为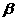 ,
,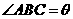 。
。
(I)
若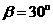 ,求
,求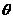 。
。
(II)
如果整个公园都建在古迹B的右侧(如图1),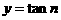 ,试探求
,试探求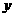 一关于
一关于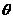 的函数关系式(不要求求出定义域)
的函数关系式(不要求求出定义域)
(III)
如果公园分布在古迹B的左右两侧(如图2),试探求公园面积S关于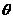 的函数并求其最小值。
的函数并求其最小值。




湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com