
题目列表(包括答案和解析)
7.若a>b>c,a+2b+3c=0,则( )
A.ab>ac B.ac>bc C.ab>bc D.a|b|>c|b|
解析:∵a>b>c且a+2b+3c=0,∴a>0,c<0.
又∵b>c且a>0,∴ab>ac.
答案:A
6.已知a,b为同号实数,且a<b,则下列命题成立的是( )
A.a2<b2
B.a2b<ab2 C.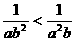 D.
D.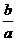 <
<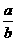
答案:B
5.设a>1,且m=loga(a2+1),n=loga(a-1),p=loga(2a),则m,n,p的大小关系为( )
A.n>m>p B.m>p>n C.m>n>p D.p>m>n
解析:因为a>1,所以a2+1>2a,2a>a-1.
又因为m=loga(a2+1),n=loga(a-1),p=loga(2a),且函数y=logax为增函数,
所以m,n,p的大小关系为m>p>n,选B.
答案:B
4.若a>0,b>0,c>0且a2+2ab+2ac+4bc=12,则a+b+c的最小值是( )
A.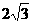 B.3 C.2
D.
B.3 C.2
D.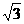
解析:(a+b+c)2=a2+b2+c2+2ab+2ac+2bc=12+(b-c)2≥12,当且仅当b=c时取等号,故选A.
答案:A
3.如果实数a,b,c满足c<b<a且ac<0,那么下列选项中不一定成立的是 ( )
A.ab>ac B.c(b-a)>0 C.ac(a-c)<0 D.cb2<ab2
解析:由已知条件,知a>0,c<0,答案中A、B、C的结论都正确,只有D中,当b2=0时,式子不成立,因此选D.
答案:D
2.若a>b,c>d,则下列不等式成立的是( )
A.a+d>b+c
B.ac>bd
C.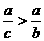 D.d-a<c-b
D.d-a<c-b
解析:因为d<c,-a<-b,所以d-a<c-b.
答案:D
1.“-1<x<1”是“x2<1”的( )
A.充要条件 B.充分但不必要条件
C.必要但不充分条件 D.既不充分也不必要条件
解析:由已知x2<1,得-1<x<1.由-1<x<1,得x2<1.所以二者是等价的,故选A.
答案:A
12.对1个单位质量的含污物体进行清洗,清洗前其清洁度(含污物体的清洁度定义为1- )为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为a(1≤a≤3).设用x单位质量的水初次清洗后的清洁度是
)为0.8,要求洗完后的清洁度是0.99.有两种方案可供选择,方案甲:一次清洗;方案乙:两次清洗.该物体初次清洗后受残留水等因素影响,其质量变为a(1≤a≤3).设用x单位质量的水初次清洗后的清洁度是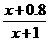 (x>a-1),用y质量的水第二次清洗后的清洁度是
(x>a-1),用y质量的水第二次清洗后的清洁度是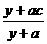 ,其中c(0.8<c<0.99)是该物体初次清洗后的清洁度.
,其中c(0.8<c<0.99)是该物体初次清洗后的清洁度.
(1)分别求出方案甲以及c=0.95时方案乙的用水量,并比较哪一种方案用水量较少;
(2)若采用方案乙,当a为某定值时,如何安排初次与第二次清洗的用水量,使总用水量最少?并讨论a取不同数值时对最少总用水量多少的影响.
解:(1)方案甲与方案乙的用水量分别为x与z,
由题设有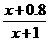 =0.99,解得x=19.
=0.99,解得x=19.
由c=0.95得方s案乙初次用水量为3,第二次用水量y满足方程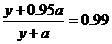 ,
,
解得y=4a,故z=4a+3,
即两种方案的用水量分别为19与4a+3.
因为当1≤a≤3时,x-z=4(4-a)>0,
即x>z,故方案乙的用水量较少.
(2)设初次与第二次清洗的用水量分别为x与y,类似(1)得
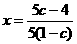 ,y=a(99-100c).(*)
,y=a(99-100c).(*)
于是,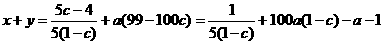 .
.
当a为定值时,x+y≥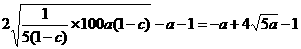 ,
,
当且仅当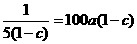 时等号成立.
时等号成立.
此时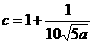 (不合题意,舍去)或
(不合题意,舍去)或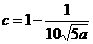 ∈(0.8,0.99),
∈(0.8,0.99),
将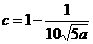 代入(*)式得
代入(*)式得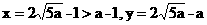 .
.
故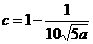 时总用水量最少,此时第一次与第二次用水量分别为
时总用水量最少,此时第一次与第二次用水量分别为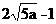 与
与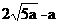 ,最少总用水量是
,最少总用水量是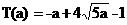 .
.
当1≤a≤3时,T′(a)=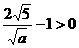 ,
,
故T(a)是增函数(也可以用二次函数的单调性判断).这说明,随着a的值的增加,最少总用水量也增加.
11.设定义在R上的函数f(x)=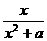 的图象的最高点为P(m,n).
的图象的最高点为P(m,n).
(1)若m<1,n<1,求a的取值范围;
(2)求证:对任意x,y∈R,|f(x)-f(y)|<1的充要条件是m>1.
(1)解:∵f(x)的定义域是R,∴a>0.
由f(x)=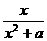 (a>0),知图象的最高点只能落在(0,+∞)内,
(a>0),知图象的最高点只能落在(0,+∞)内,
于是,f(x)=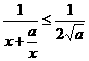 ,
,
当且仅当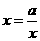 ,即
,即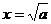 时,f(x)max=
时,f(x)max=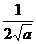 .
.
又m<1,n<1,即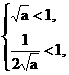 ∴
∴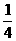 <a<1.
<a<1.
(2)证明:∵f(x) max=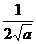 ,f(x)是奇函数,
,f(x)是奇函数,
∴f(x)
min=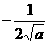 .
.
∴|f(x)-f(y)|≤|f(x)max-f(x)min|
=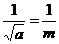 .
.
对任意x,y∈R,|f(x)-f(y)|<1
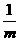 <1
<1 m>1.
m>1.
10.已知p: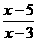 ≥2,q:x2-ax≤x-a,若
≥2,q:x2-ax≤x-a,若 p是
p是 q的充分条件,求实数a的取值范围.
q的充分条件,求实数a的取值范围.
解:由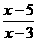 ≥2,得
≥2,得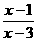 ≤0,∴1≤x<3.
≤0,∴1≤x<3.
由x2-ax≤x-a,得(x-a)(x-1)≤0.
(1)当a<1时,a≤x≤1;
(2)当a=1时,x=1;
(3)当a>1时,1≤x≤a.∵ p
p q的充分条件,
q的充分条件,
∴q是p的充分条件.
设p对应集合A,q对应集合B,则A={x|1≤x<3}且B A.
A.
当a<1时,B={x|a≤x≤1},B A,不符合题意;
A,不符合题意;
当a=1时,B={x|x=1},B A,符合题意;
A,符合题意;
当a>1时,B={x|1≤x≤a},要B A,需1<a<3.
A,需1<a<3.
综上,得1≤a<3.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com