
题目列表(包括答案和解析)
7.直线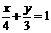 与椭圆
与椭圆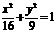 相交于A、B两点,该椭圆上点P,使得△APB的面积等于3,这样的点P共有
相交于A、B两点,该椭圆上点P,使得△APB的面积等于3,这样的点P共有
A.1个 B.2 C.3个 D.4个
6.等边三角形ABC和等边三角形ABD在两个相互垂直的平面内,则∠CAD=
A.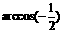 B.
B.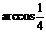 C.
C.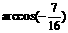 D.
D.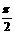
5.已知θ∈(-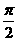 ,
,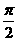 ),且sinθ+cosθ=a,其中a∈(0,1),则关于tanθ的值,以下四个选项中,可能正确的是
),且sinθ+cosθ=a,其中a∈(0,1),则关于tanθ的值,以下四个选项中,可能正确的是
A.-3 B.3或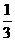 C.-
C.- 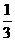 D.-3或-
D.-3或- 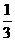
4.已知函数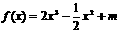 (
( 为常数)图象上A处的切线与
为常数)图象上A处的切线与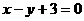 的夹角为
的夹角为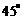 ,则A点的横坐标为
,则A点的横坐标为
A.0 B.1 C.0或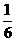 D.1或
D.1或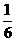
3.已知方程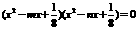 的四个根组成一个首项为
的四个根组成一个首项为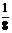 的等比数列,则
的等比数列,则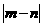 =
=
A. 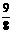 B. 1 C.
B. 1 C.
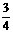 D.
D. 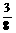
2.如果直线x-3y=7和y=kx-2与x轴正半轴、y轴所围成的四边形有外接圆,那么k的值为
A.-3或3 B.-3或-6 c.3或6 D.-6或6
1.下列各数中,与sin20080的值最接近的是
A.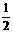 B.
B.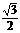 C.-
C.-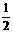 D.-
D.-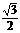
21.已知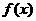 是定义在褛实数集R上恒不为零的函数,且对任意实数
是定义在褛实数集R上恒不为零的函数,且对任意实数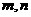 ,恒有
,恒有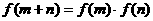 .
.
(1)若当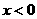 时,
时,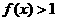 ,证明
,证明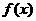 是R上的减函数;(2)设
是R上的减函数;(2)设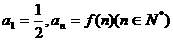 ,数列
,数列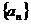 的前
的前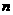 项和为
项和为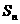 ,求证:
,求证: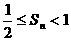 ;(3)在(1)的条件下,设集合
;(3)在(1)的条件下,设集合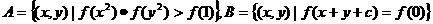 ,若
,若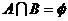 ,求实数
,求实数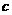 的取值范围.
的取值范围.
解:(1)设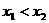 ,因为
,因为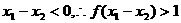 。
。
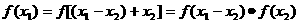 ,因为
,因为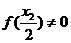 ,所以
,所以
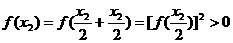 ,所以
,所以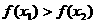 ,即
,即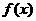 是R上的减函数
是R上的减函数
(2)因为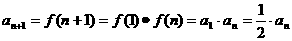 ,所以
,所以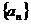 是等比数列,其中
是等比数列,其中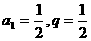 ,所以
,所以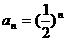 。
。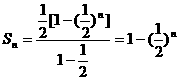 ,所以
,所以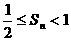
(3)在(1)的条件下,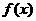 在R上是减函数,由
在R上是减函数,由
由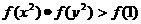 ,得
,得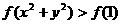 ,所以
,所以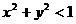 ,即
,即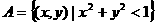 ,由
,由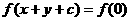 得
得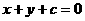 ,即
,即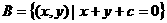 ,因为
,因为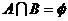 ,所以由图形分析知:直线
,所以由图形分析知:直线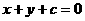 与圆
与圆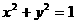 相离或相切。所以
相离或相切。所以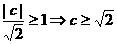 或
或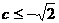 .
.
20.已知抛物线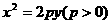 的焦点为F,A是抛物线上一点,且纵坐标为4,A到抛物线准线的距离为5.
的焦点为F,A是抛物线上一点,且纵坐标为4,A到抛物线准线的距离为5.
(1)求抛物线的方程;(2)过点M(2,-1)作抛物线的两条切线与抛物线分别切于B、C两点,求证: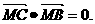
解:(1)由题意知,抛物线的方程为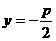 ,
,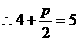 ,得
,得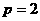 ,所以抛物线方程为
,所以抛物线方程为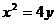
(2)设切线方程为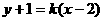 ,代入抛物线方程可得:
,代入抛物线方程可得: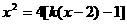 ,整理得:
,整理得: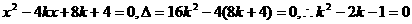
所以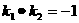 ,即过点M有两条切线,且互相垂直,所以
,即过点M有两条切线,且互相垂直,所以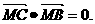 (或用求导方法解答)
(或用求导方法解答)
19.已知函数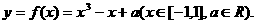
(1)求函数的值域;(2)设函数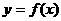 的定义域为D,若对任意的
的定义域为D,若对任意的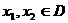 ,都有
,都有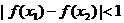 成立,则称函数
成立,则称函数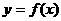 为“涟源一中函数”,否则称为“非涟源一中函数”.试判断函数
为“涟源一中函数”,否则称为“非涟源一中函数”.试判断函数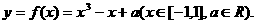 是否为“涟源一中函数”,如果是,请给出证明,如果不是,请说明理由.
是否为“涟源一中函数”,如果是,请给出证明,如果不是,请说明理由.
解:(1)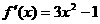 ,令
,令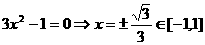
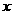 |
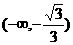 |
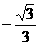 |
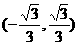 |
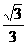 |
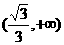 |
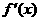 |
+ |
0 |
- |
0 |
+ |
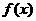 |
增函数 |
极大值 |
减函数 |
极小值 |
增函数 |
又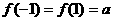 可见,当
可见,当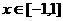 时,
时,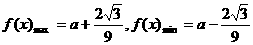
所以函数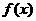 的值域为
的值域为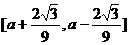
(2)如果对于任意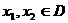 ,都有
,都有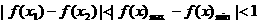 成立,即可证明函数
成立,即可证明函数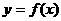 是“涟源一中函数”,否则
是“涟源一中函数”,否则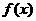 为“非涟源一中函数”.
为“非涟源一中函数”.
因为 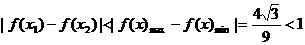 ,所以函数
,所以函数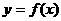 是“涟源一中函数”。
是“涟源一中函数”。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com