
题目列表(包括答案和解析)
4.解:(1)建立如图所示的坐标系,则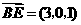 ,
,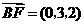 ,
,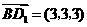 ,
,
 所以
所以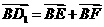 ,故
,故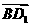 ,
,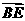 ,
,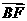 共面.
共面.
又它们有公共点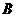 ,所以
,所以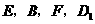 四点共面.
四点共面.
(2)如图,设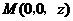 ,则
,则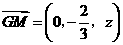 ,
,
而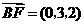 ,由题设得
,由题设得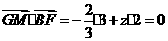 ,
,
得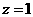 .因为
.因为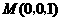 ,
,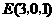 ,有
,有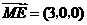 ,
,
又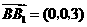 ,
,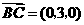 ,所以
,所以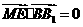 ,
,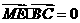 ,从而
,从而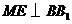 ,
,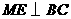 .
.
故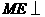 平面
平面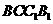 .
.
(3)设向量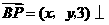 截面
截面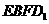 ,于是
,于是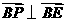 ,
,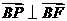 .
.
而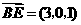 ,
,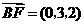 ,得
,得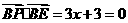 ,
,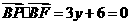 ,解得
,解得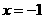 ,
,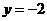 ,所以
,所以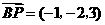 .
.
又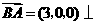 平面
平面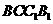 ,于是
,于是 .故
.故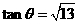 .
.
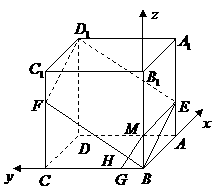
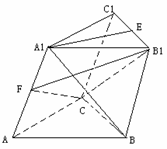
4. 如图,已知
如图,已知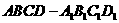 是棱长为3的正方体,
是棱长为3的正方体,
点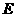 在
在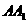 上,点
上,点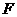 在
在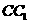 上,且
上,且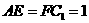 ,
,
(1)求证: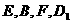 四点共面;
四点共面;
(2)若点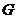 在
在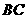 上,
上,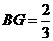 ,点
,点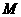 在
在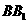 上,
上,
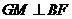 ,垂足为
,垂足为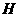 ,求证:
,求证: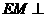 面
面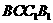 ;
;
(3)用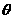 表示截面
表示截面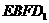 和面
和面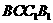 所成锐二面角大小,求
所成锐二面角大小,求 。
。
3.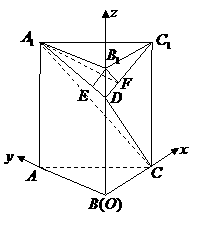 解:(Ⅰ)以
解:(Ⅰ)以 点为坐标原点
点为坐标原点 建立空间直角坐标系
建立空间直角坐标系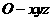 ,则
,则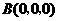 ,
,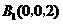 ,
,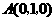 ,
,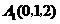 ,则
,则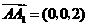 ,
,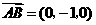 .设
.设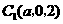 ,则
,则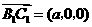 ,
,
又设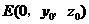 ,则
,则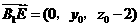 ,
,
从而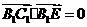 ,即
,即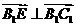 .
.
又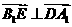 ,所以
,所以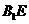 是异面直线
是异面直线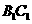 与
与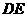 的公垂线.
的公垂线.
设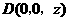 ,则
,则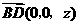 .因四棱锥
.因四棱锥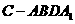 的体积
的体积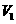 为
为
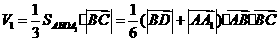
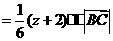 .
.
而直三棱柱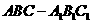 的体积
的体积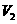 为
为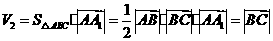 .
.
由已知条件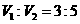 ,故
,故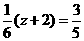 ,解得
,解得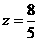 ,即
,即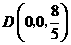 .
.
从而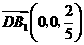 ,
,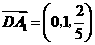 ,
,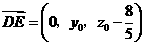 .
.
由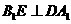 ,有
,有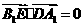 ,即
,即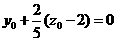 (1)
(1)
又由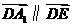 得
得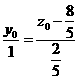 . (2)
. (2)
联立(1),(2),解得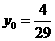 ,
,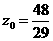 ,即
,即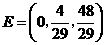 ,得
,得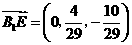 .
.
故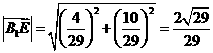 .
.
(Ⅱ)由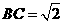 ,得
,得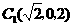 ,
,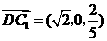 ,过
,过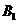 作
作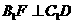 ,垂足为
,垂足为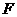 ,连接
,连接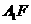 ,
,
设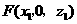 ,则
,则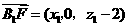 ,因为
,因为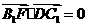 ,故
,故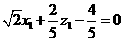 ………①
………①
因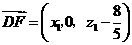 且
且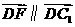 得
得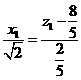 ,即
,即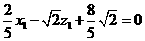 …………②
…………②
联立①②解得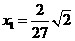 ,
,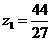 ,即
,即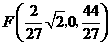 .
.
则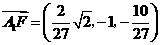 ,
,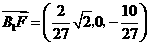 .
. 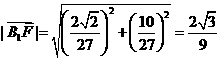 .
.
又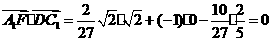 ,故
,故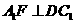 ,因此
,因此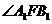 为所求二面角的平面角.又
为所求二面角的平面角.又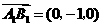 ,从而
,从而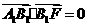 ,故
,故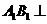
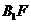 ,
,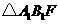 为直角三角形,所以
为直角三角形,所以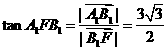 .
.
3.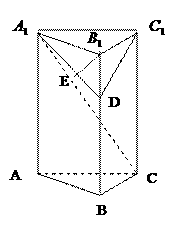 如图,在直三棱柱ABC-
如图,在直三棱柱ABC-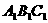 中,
中,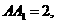 AB = 1,
AB = 1,
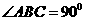 ;点D、E分别在
;点D、E分别在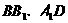 上,且
上,且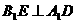 ,
,
四棱锥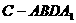 与直三棱柱的体积之比为3:5。
与直三棱柱的体积之比为3:5。
(1)求异面直线DE与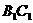 的距离;
的距离;
(2)若BC =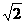 ,求二面角
,求二面角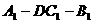 的平面角的正切值。
的平面角的正切值。
2.
如图,四棱锥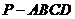 中,侧面
中,侧面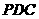 是边长为2的正三角形,且与底面垂直,底面
是边长为2的正三角形,且与底面垂直,底面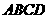 是
是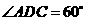 的菱形,
的菱形,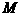 为
为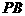 的中点.
的中点.
(Ⅰ)求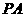 与底面
与底面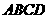 所成角的大小;
所成角的大小;
(Ⅱ)求证: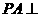 平面
平面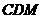 ;
;
(Ⅲ)求二面角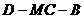 的余弦值.
的余弦值.
解析:求线面角关键是作垂线,找射影,求异面直线所成的角采用平移法 求二面角的大小也可应用面积射影法,比较好的方法是向量法
求二面角的大小也可应用面积射影法,比较好的方法是向量法
答案:(I)取DC的中点O,由ΔPDC是正三角形,有PO⊥DC.
又∵平面PDC⊥底面ABCD,∴PO⊥平面ABCD于O.
连结OA,则OA是PA在底面上的射影.∴∠PAO就是PA与底面所成角.
∵∠ADC=60°,由已知ΔPCD和ΔACD是全等的正三角形,从而求得OA=OP=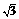 .
.
∴∠PAO=45°.∴PA与底面ABCD可成角的大小为45°. ……6分
(II)由底面ABCD为菱形且∠ADC=60°,DC=2,DO=1,有OA⊥DC.
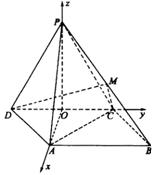 建立空间直角坐标系如图,则
建立空间直角坐标系如图,则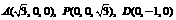 ,
, 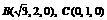 .
.
由M为PB中点,∴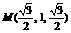 .
.
∴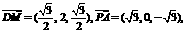
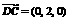 .
.
∴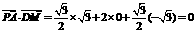 ,
,
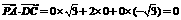 .
.
∴PA⊥DM,PA⊥DC. ∴PA⊥平面DMC. ……4分
(III)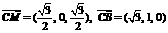 .令平面BMC的法向量
.令平面BMC的法向量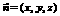 ,
,
则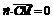 ,从而x+z=0;
……①,
,从而x+z=0;
……①,
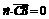 ,从而
,从而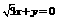 . ……②
. ……②
由①、②,取x=−1,则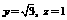 . ∴可取
. ∴可取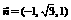 .
.
由(II)知平面CDM的法向量可取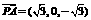 ,
,
∴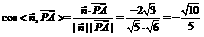 . ∴所求二面角的余弦值为-
. ∴所求二面角的余弦值为-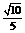 . ……6分
. ……6分
法二:(Ⅰ)方法同上
(Ⅱ)取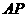 的中点
的中点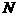 ,连接
,连接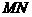 ,由(Ⅰ)知,在菱形
,由(Ⅰ)知,在菱形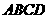 中,由于
中,由于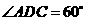 ,则
,则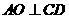 ,又
,又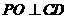 ,则
,则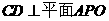 ,即
,即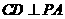 ,
,
又在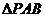 中,中位线
中,中位线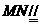
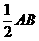 ,
,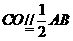 ,则
,则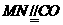 ,则四边形
,则四边形 为
为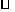 ,所以
,所以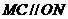 ,在
,在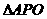 中,
中,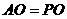 ,则
,则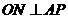 ,故
,故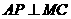 而
而 ,
,
则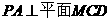
(Ⅲ)由(Ⅱ)知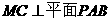 ,则
,则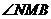 为二面角
为二面角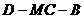 的平面角,在
的平面角,在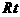
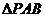 中,易得
中,易得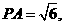
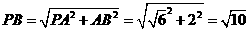 ,
,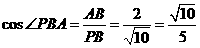 ,
,
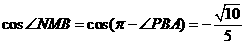 故,所求二面角的余弦值为
故,所求二面角的余弦值为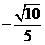
1. 如图, 在直三棱柱ABC-A1B1C1中,AC=3,BC=4,AA1=4,点D是AB的中点, (I)求证:AC⊥BC1; (II)求证:AC 1//平面CDB1;
解析:(1)证明线线垂直方法有两类:一是通过三垂线定理或逆定理证明,二是通过线面垂直来证明线线垂直;(2)证明线面平行也有两类:一是通过线线平行得到线面平行,二是通过面面平行得到线面平行.
答案:解法一:(I)直三棱柱ABC-A1B1C1,底面三边长AC=3,BC=4AB=5,
∴ AC⊥BC,且BC1在平面ABC内的射影为BC,∴ AC⊥BC1;
(II)设CB1与C1B的交点为E,连结DE,∵ D是AB的中点,E是BC1的中点,
∴ DE//AC1, ∵ DE
∵ DE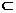 平面CDB1,AC1
平面CDB1,AC1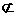 平面CDB1,
平面CDB1,
∴ AC1//平面CDB1;
解法二:∵直三棱柱ABC-A1B1C1底面三边长AC=3,BC=4,AB=5,∴AC、BC、C1C两两垂直,如图,以C为坐标原点,直线CA、CB、C1C分别为x轴、y轴、z轴,建立空间直角坐标系,则C(0,0,0),A(3,0,0),C1(0,0,4),B(0,4,0),B1(0,4,4),D(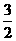 ,2,0)
,2,0)
(1)∵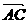 =(-3,0,0),
=(-3,0,0),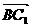 =(0,-4,0),∴
=(0,-4,0),∴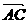 •
•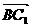 =0,∴AC⊥BC1.
=0,∴AC⊥BC1.
 (2)设CB1与C1B的交战为E,则E(0,2,2).∵
(2)设CB1与C1B的交战为E,则E(0,2,2).∵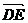 =(-
=(-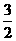 ,0,2),
,0,2),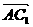 =(-3,0,4),∴
=(-3,0,4),∴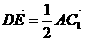 ,∴DE∥AC1.
,∴DE∥AC1.
点评:2.平行问题的转化:
|
|
面面平行 线面平行
线面平行 线线平行;
线线平行;

22. 已知二次函数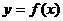 经过点(0,10),其导数
经过点(0,10),其导数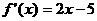 ,当
,当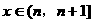 (
(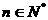 )时,
)时,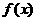 是整数的个数记为
是整数的个数记为 。
。
(1)求数列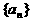 的通项公式;
的通项公式;
(2)令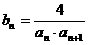 ,求数列
,求数列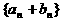 的前n项(
的前n项(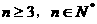 )项和
)项和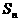 。
。
21.设椭圆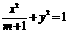 的两个焦点是
的两个焦点是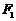 、
、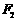 。Ⅰ)若在直线
。Ⅰ)若在直线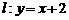 上存在一点
上存在一点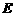 ,且点
,且点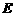 在椭圆上,使得
在椭圆上,使得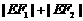 取得最小值,求此最小值及此时椭圆的方程;
取得最小值,求此最小值及此时椭圆的方程;
Ⅱ)在条件(Ⅰ)下的椭圆方程,是否存在斜率为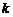 (
(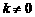 )的直线
)的直线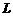 与椭圆交于不同的两点
与椭圆交于不同的两点 、
、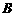 ,满足
,满足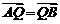 ,且使得过点
,且使得过点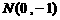 和
和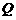 的直线有
的直线有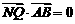 ?若存在,求出
?若存在,求出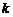 的取值范围;若不存在,说明理由。
的取值范围;若不存在,说明理由。
20. 设事件A发生的概率为p,若在A发生的条件下B发生的概率为p′,则由A产生B的概率为p·p′.根据这一事实解答下题.
一种掷硬币走跳棋的游戏:棋盘上有第0、1、2、…、100,共101站,设棋子跳到第n站时的概率为p ,一枚棋子开始在第0站(即p
,一枚棋子开始在第0站(即p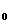 =1),由棋手每掷一次硬币,棋子向前跳动一次.若硬币出现正面则棋子向前跳动一站,出现反面则向前跳动两站.直到棋子跳到第99站(获胜)或第100站(失败)时,游戏结束.已知硬币出现正反面的概率都为.
=1),由棋手每掷一次硬币,棋子向前跳动一次.若硬币出现正面则棋子向前跳动一站,出现反面则向前跳动两站.直到棋子跳到第99站(获胜)或第100站(失败)时,游戏结束.已知硬币出现正反面的概率都为.
(1)求p1,p2,p3,并根据棋子跳到第n+1站的情况,试用pn,pn-1表示pn+1;
(2)求玩该游戏获胜的概率
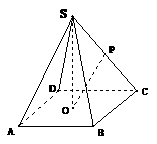
19.如图,已知四棱锥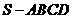 的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,且O到AB、AD的距离分别为2、1。
的底面是边长为4的正方形,S在底面上的射影O落在正方形ABCD内,且O到AB、AD的距离分别为2、1。
(1)求证: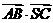 是定值;
是定值;
(2)已知P是SC的中点,且SO=3,问在棱SA上是否存在一点Q,使异面直线OP与BQ所成的角为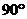 ?若不存在,则说明原因;若存在,则求出AQ的长。
?若不存在,则说明原因;若存在,则求出AQ的长。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com