
题目列表(包括答案和解析)
18.已知正项数列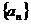 中,
中,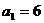 ,点
,点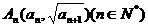 在抛物线
在抛物线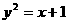 上,有数列
上,有数列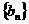 ,点
,点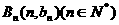 在过点(0,1),以
在过点(0,1),以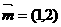 为方向向量的直线
为方向向量的直线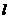 上.
上.
(1)求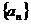 ,
,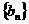 的通项公式;(2)若
的通项公式;(2)若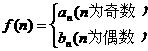 ,问是否存在
,问是否存在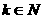 ,使
,使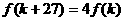 成立.
成立.
解:(1)将点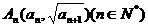 代入
代入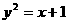 中,得
中,得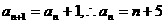
因为直线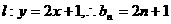 。
。
(2)当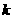 为偶数时,
为偶数时,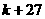 为奇数,所以
为奇数,所以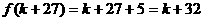
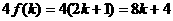 ,由
,由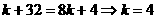 。
。
当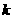 为奇数时,
为奇数时,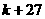 为偶数,
为偶数,
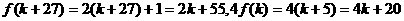
由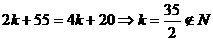 ,故存在唯一的
,故存在唯一的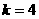 符合题意。
符合题意。
17.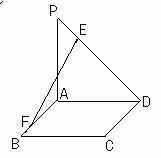 如图,ABCD是矩形,PA
如图,ABCD是矩形,PA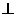 平面ABCD,PA=AD=
平面ABCD,PA=AD=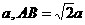 ,E是线段PD上的点,F是线段AB上的点,且
,E是线段PD上的点,F是线段AB上的点,且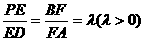 .
.
(1)当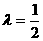 时,求直线EF与平面ABCD所成的角的正弦值;
时,求直线EF与平面ABCD所成的角的正弦值;
(2)是否存在实数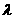 ,使AC
,使AC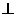 EF?若存在,试求出
EF?若存在,试求出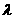 的值.若不存在,请说明理由.
的值.若不存在,请说明理由.
法一:(1)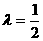 时,
时,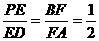 ,又PA
,又PA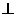 平面ABCD,过E作EM
平面ABCD,过E作EM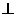 AD于M,则EM
AD于M,则EM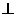 平面ABCD,连FM,则
平面ABCD,连FM,则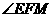 为直线EF与平面ABCD所成的角。
为直线EF与平面ABCD所成的角。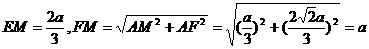 ,在直角三角形EFM中,
,在直角三角形EFM中,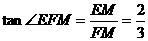 ,所以
,所以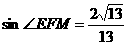 。
。
(2)设存在实数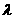 ,使AC
,使AC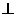 EF,因为EM
EF,因为EM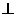 平面ABCD,所以EM
平面ABCD,所以EM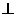 AC,AC
AC,AC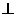 FM,设AC交FM于O点,则
FM,设AC交FM于O点,则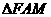 ∽
∽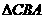 ,所以
,所以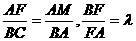 ,所以
,所以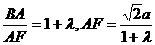 ,
,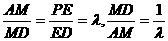 ,所以
,所以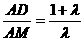 ,从而
,从而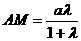 ,所以有
,所以有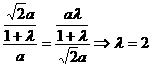
法二:以A为坐标原点,分别以AB、AD、AF所在直线为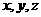 建立空间直角坐标系。具体过程略
建立空间直角坐标系。具体过程略
16.设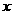 为
为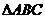 的一个内角,函数
的一个内角,函数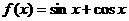 .
.
(1)求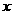 为何值时,
为何值时,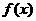 有最大值,并求出该最大值;(2)若
有最大值,并求出该最大值;(2)若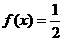 ,求
,求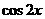 的值;
的值;
解:(1)因为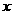 为
为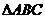 的一个内角,所以
的一个内角,所以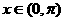 ,
,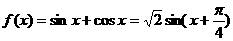
所以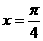 时,
时,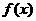 有最大值为
有最大值为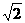 。
。
(2)由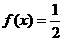 ,所以
,所以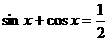 ,两边平方得
,两边平方得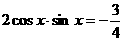 ,即
,即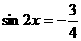
因为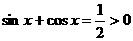 ,所以
,所以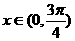 ,又
,又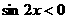 ,所以
,所以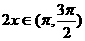
故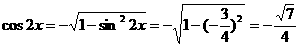
15.定义一种新运算“*”,对任意正整数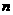 ,满足(1)
,满足(1)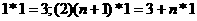 ,则2003*1的值为
6009
,则2003*1的值为
6009
14.当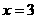 时,不等式
时,不等式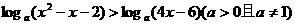 成立,则此不等式的解集为 (2,4)
成立,则此不等式的解集为 (2,4)
13.点P在曲线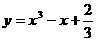 上移动,在点P处的切线的倾斜角为
上移动,在点P处的切线的倾斜角为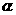 ,则
,则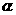 的取值范围是
的取值范围是 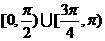 .
.
12.已知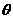 为三角形的内角,
为三角形的内角,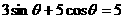 ,则
,则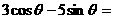 -3
.
-3
.
11.函数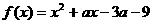 对任意
对任意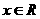 恒有
恒有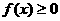 ,则
,则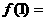 4
4
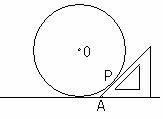
10.如图所示,水平地面上有一个大球,现有如下方法测量球的大小,用一个锐角为45度的三角板,斜边紧靠球面,一条直角边紧靠地面,并使三角板与地面垂直,如果测得PA=5 ,则球的表面积是( B )
,则球的表面积是( B )
 (A)
(A)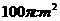 (B)
(B)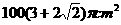
(C)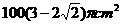 (D)
(D)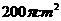
9.将一枚骰子抛掷两次,若先后出现的点数分别为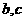 ,则方程
,则方程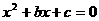 有相等实根的概率为( D )
有相等实根的概率为( D )
(A)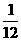 (B)
(B)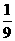 (C)
(C)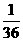 (D)
(D)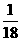
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com