
题目列表(包括答案和解析)
3.(2010重庆文)(8)若直线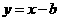 与曲线
与曲线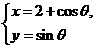 (
(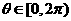 )有两个不同的公共点,则实数
)有两个不同的公共点,则实数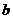 的取值范围为
的取值范围为
(A)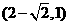 (B)
(B)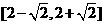
(C) (D)
(D)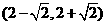
[答案]D
解析: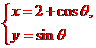 化为普通方程
化为普通方程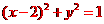 ,表示圆,
,表示圆,
 因为直线与圆有两个不同的交点,所以
因为直线与圆有两个不同的交点,所以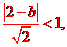 解得
解得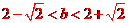
法2:利用数形结合进行分析得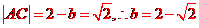
同理分析,可知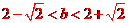
2.(2010安徽文)(4)过点(1,0)且与直线x-2y-2=0平行的直线方程是
(A)x-2y-1=0 (B)x-2y+1=0 (C)2x+y-2=0 (D)x+2y-1=0
[答案]A
[解析]设直线方程为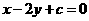 ,又经过
,又经过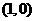 ,故
,故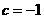 ,所求方程为
,所求方程为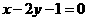 .
.
[方法技巧]因为所求直线与与直线x-2y-2=0平行,所以设平行直线系方程为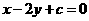 ,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.
,代入此直线所过的点的坐标,得参数值,进而得直线方程.也可以用验证法,判断四个选项中方程哪一个过点(1,0)且与直线x-2y-2=0平行.
1.(2010江西理)8.直线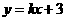 与圆
与圆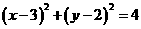 相交于M,N两点,若
相交于M,N两点,若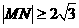 ,则k的取值范围是
,则k的取值范围是
A. 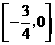 B.
B.
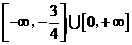 C.
C. 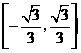 D.
D.
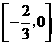
[答案]A
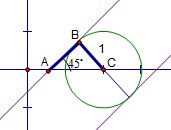
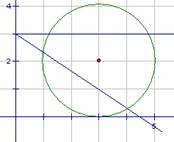 [解析]考查直线与圆的位置关系、点到直线距离公式,重点考察数形结合的运用.
[解析]考查直线与圆的位置关系、点到直线距离公式,重点考察数形结合的运用.
解法1:圆心的坐标为(3.,2),且圆与y轴相切.当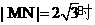 ,由点到直线距离公式,解得
,由点到直线距离公式,解得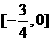 ;
;
解法2:数形结合,如图由垂径定理得夹在两直线之间即可,
不取 ,排除B,考虑区间不对称,排除C,利用斜率估值,选A
,排除B,考虑区间不对称,排除C,利用斜率估值,选A
2010年高考题
12、已知点P(sinx-cosx ,tgx)在第一象限,则在[0,2π)内x的取值范围是
11、若sinθ=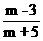 ,cosθ=
,cosθ=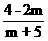 ,θ∈
,θ∈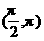 ,则m的取值是( )
,则m的取值是( )
(A)3<m<9 (B)m=8 (C)m>3 (D)m<9
10、已知sin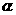 cos
cos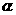 =
=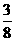 ,且
,且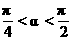 则cos
则cos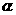 -sin
-sin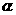 的值为( )
的值为( )
(A)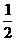 (B)-
(B)-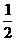 (C)
(C)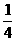 (D)-
(D)-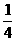
9、已知θ是第二象限的角,且sin4θ+cos4θ=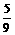 ,那么sin2θ等于( )
,那么sin2θ等于( )
(A)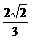 (B)-
(B)-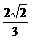 (C)
(C)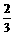 (D)-
(D)-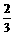
8、若角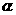 满足条件
满足条件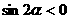 ,
,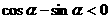 ,则
,则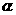 在( )
在( )
(A)第一象限 (B)第二象限 (C)第三象限 (D)第四象限
7、函数y=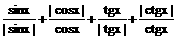 的值域是( )
(A){-2,4} (B){-2,0,4} (C){-2,0,2,4} (D){-4,-2,0,4}
的值域是( )
(A){-2,4} (B){-2,0,4} (C){-2,0,2,4} (D){-4,-2,0,4}
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com