
题目列表(包括答案和解析)
4、已知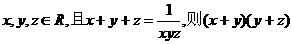 的最小值为 .
的最小值为 .
3、已知函数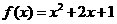 ,若存在实数
,若存在实数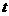 ,当
,当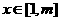 时
时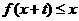 恒成立,则实数
恒成立,则实数 的最大值为
的最大值为
(A) 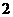 (B)
(B)
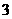 (C)
(C)
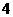 (D)
(D)
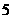
2、命题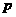 :关于
:关于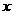 的不等式
的不等式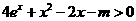 对于一切实数
对于一切实数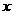 均成立,命题
均成立,命题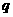 :
: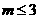 ,则
,则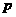 是
是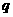 成立的( )。
成立的( )。
(A) 充分而不必要条件 (B) 必要而不充分条件
(C) 充分必要条件 (D) 既不充分也不必要条件
两边夹的方法,对于解决不能通过计算准确求解的不等式问题是一种很好的方法。在以前的高考中也曾出现过。这种方法很好的考查了学生的思维。
例5.已知函数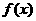 满足
满足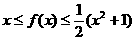 ,对一切实数
,对一切实数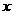 恒成立,则
恒成立,则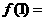
分析:因为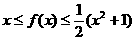 对一切实数
对一切实数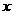 恒成立,不妨令
恒成立,不妨令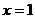 ,则有
,则有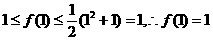 。
。
另外,还有构造法及一些特殊不等式如柯西不等式.有兴趣的同学可以参考一些课外资料学习一下.
跟踪练习:
1、已知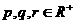 ,则
,则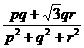 的最大值为( )。
的最大值为( )。
 A、1 B、2 C、
A、1 B、2 C、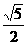 D、
D、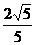
例4. 已知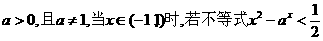 恒成立,则
恒成立,则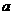 的取值范围为 .
的取值范围为 .
分析: 此不等式是一个超越不等式,要求出a的范围有些同学可能会想到反解a,但是这显然做不到。这样我们不妨将原不等式变形为
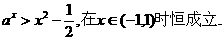
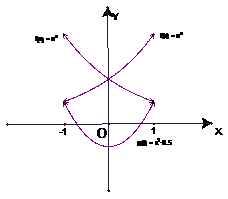 设函数
设函数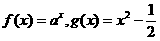 ,这两个函数我们还是较熟悉的。在同一坐标系内,分别作出它们的图像。由函数的单调性及图像可知:
,这两个函数我们还是较熟悉的。在同一坐标系内,分别作出它们的图像。由函数的单调性及图像可知:
当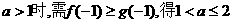
当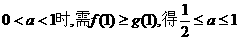 .故
.故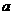 的取值范围为
的取值范围为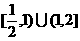 .
.
例3. 设实数a使得不等式|2x−a|+|3x−2a|≥a2对任意实数x恒成立,则满足条件的a所组成的集合是( )
A. 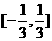 B.
B. 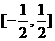 C.
C. 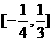 D. [−3,3]
D. [−3,3]
分析:我们可用附值法可若令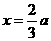 ,则有
,则有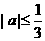 ,排除B、D。由对称性排除C,从而只有A正确。注意若仅令x=0或
,排除B、D。由对称性排除C,从而只有A正确。注意若仅令x=0或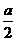 将会得到错误结果。
将会得到错误结果。
我们有更一般的解决方法吗?对k∈R,不妨令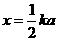 ,(当然也可令
,(当然也可令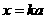 ),则原不等式为
),则原不等式为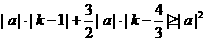 ,
,
由此易知原不等式等价于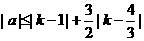 ,对任意的k∈R成立。由于
,对任意的k∈R成立。由于
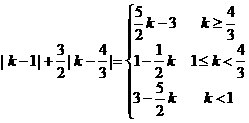 ,
,
所以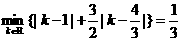 ,从而上述不等式等价于
,从而上述不等式等价于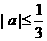 。
。
例2、已知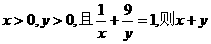 的最小值为
。
的最小值为
。
分析:有些不等式问题中在求最值和范围时要利用常数“1”的代换技巧
解: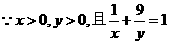 ,
,
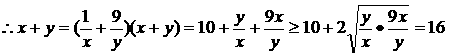 ,
,
当且仅当
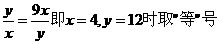 .故最小值为16.
.故最小值为16.
评析:本题除此法外,还可以用三角换元的方法。
例1设x、y、z都是正数,则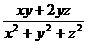 的最大值为( )。
的最大值为( )。
A、1 B、2 C、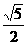 D、
D、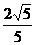
分析:在我们用均值不等式时,经常会用到配凑系数来求最值。显然如果我们直接处理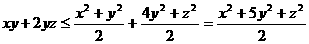 ,显然与分母的比值不是常数。我们很希望通过利用均值不等式将分子中
,显然与分母的比值不是常数。我们很希望通过利用均值不等式将分子中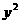 的系数调整为1,如何实现这个目标呢?我们注意到
的系数调整为1,如何实现这个目标呢?我们注意到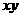 的系数为1,而
的系数为1,而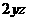 的系数为2。联想到三角函数中的化一公式(或称辅助角公式),
的系数为2。联想到三角函数中的化一公式(或称辅助角公式),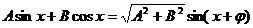 ,(其中
,(其中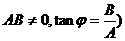 。我们不妨可以借鉴这里所使用的方法来处理,从而对y的系数进行调整。提出
。我们不妨可以借鉴这里所使用的方法来处理,从而对y的系数进行调整。提出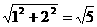 来,这样
来,这样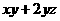
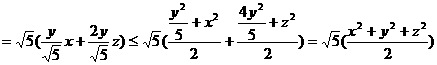 。这样y2的系数调整成1,分子与分母的比值为常数
。这样y2的系数调整成1,分子与分母的比值为常数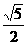 。也实现了我们的最初目的。这里我们处理的手段就是配凑系数。
。也实现了我们的最初目的。这里我们处理的手段就是配凑系数。
解法略。
14.函数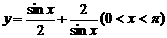 的最小值是
.
的最小值是
.
13.对任意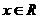 ,不等式
,不等式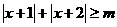 恒成立,则m的取值范围是
.
恒成立,则m的取值范围是
.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com