
题目列表(包括答案和解析)
3.(重庆文,1)圆心在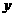 轴上,半径为1,且过点(1,2)的圆的方程为( )
轴上,半径为1,且过点(1,2)的圆的方程为( )
A.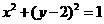 B.
B.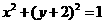
C.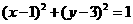 D.
D.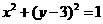
解法1(直接法):设圆心坐标为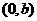 ,则由题意知
,则由题意知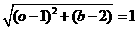 ,解得
,解得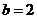 ,故圆的方程为
,故圆的方程为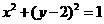 。
。
解法2(数形结合法):由作图根据点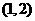 到圆心的距离为1易知圆心为(0,2),故圆的方程为
到圆心的距离为1易知圆心为(0,2),故圆的方程为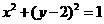
解法3(验证法):将点(1,2)代入四个选择支,排除B,D,又由于圆心在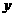 轴上,排除C。
轴上,排除C。
[答案]A
2.(重庆理,1)直线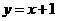 与圆
与圆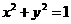 的位置关系为( )
的位置关系为( )
A.相切 B.相交但直线不过圆心 C.直线过圆心 D.相离
[解析]圆心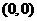 为到直线
为到直线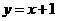 ,即
,即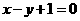 的距离
的距离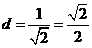 ,而
,而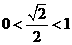 ,选B。
,选B。
[答案]B
1.(辽宁理,4)已知圆C与直线x-y=0 及x-y-4=0都相切,圆心在直线x+y=0上,则圆C的方程为
A.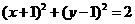 B.
B. 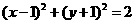
C.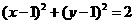 D.
D. 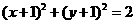
[解析]圆心在x+y=0上,排除C、D,再结合图象,或者验证A、B中圆心到两直线的距离等于半径即可.
[答案]B
12.(2010江苏卷)9、在平面直角坐标系xOy中,已知圆 上有且仅有四个点到直线12x-5y+c=0的距离为1,则实数c的取值范围是___________
上有且仅有四个点到直线12x-5y+c=0的距离为1,则实数c的取值范围是___________
[解析]考查圆与直线的位置关系。 圆半径为2,
圆心(0,0)到直线12x-5y+c=0的距离小于1,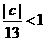 ,
,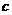 的取值范围是(-13,13)。
的取值范围是(-13,13)。
2009年高考题
11.(2010湖南理)
10.(2010山东理)

[解析]由题意,设所求的直线方程为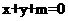 ,设圆心坐标为
,设圆心坐标为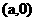 ,则由题意知:
,则由题意知:
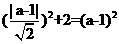 ,解得
,解得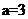 或-1,又因为圆心在x轴的正半轴上,所以
或-1,又因为圆心在x轴的正半轴上,所以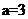 ,故圆心坐标为(3,0),因为圆心(3,0)在所求的直线上,所以有
,故圆心坐标为(3,0),因为圆心(3,0)在所求的直线上,所以有 ,即
,即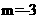 ,故所求的直线方程为
,故所求的直线方程为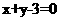 。
。
[命题意图]本题考查了直线的方程、点到直线的距离、直线与圆的关系,考查了同学们解决直线与圆问题的能力。
9.(2010四川文)(14)直线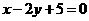 与圆
与圆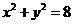 相交于A、B两点,则
相交于A、B两点,则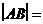 .
.
[答案]2
解析:方法一、圆心为(0,0),半径为2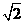 圆心到直线
圆心到直线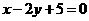 的距离为d=
的距离为d=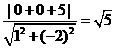 故
故
得|AB|=2
12.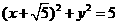 .设圆心为
.设圆心为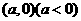 ,则
,则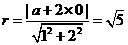 ,解得
,解得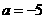 .
.
8.(2010广东理)12.已知圆心在x轴上,半径为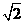 的圆O位于y轴左侧,且与直线x+y=0相切,则圆O的方程是
的圆O位于y轴左侧,且与直线x+y=0相切,则圆O的方程是
7.(2010天津文)(14)已知圆C的圆心是直线x-y+1=0与x轴的交点,且圆C与直线x+y+3=0相切。则圆C的方程为 。
[答案]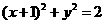
本题主要考查直线的参数方程,圆的方程及直线与圆的位置关系等基础知识,属于容易题。
令y=0得x=-1,所以直线x-y+1=0,与x轴的交点为(-1.0)
因为直线与圆相切,所以圆心到直线的距离等于半径,即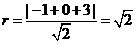 ,所以圆C的方程为
,所以圆C的方程为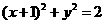
[温馨提示]直线与圆的位置关系通常利用圆心到直线的距离或数形结合的方法求解。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com