3．(2010·湖南高考)在Rt△ABC中，∠C＝90°，AC＝4，则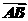·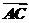等于(　)

A．－16　 　　　　　　　　　 B．－8

C．8　 　　　　　　　　　　　　 D．16

解析：法一：因为cosA＝，

故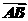·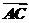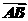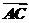＝||||cosA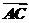＝||²＝16.

法二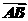：在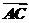上的投影为|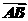|cosA＝||，

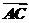故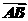·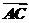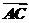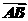＝||||cosA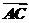＝||²＝16.

答案：D

2．在四边形ABCD中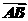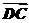，＝，且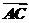·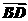＝0，则四边形ABCD是(　)

A．矩形　 　　　　　　　　　　　　 B．菱形

C．直角梯形　 　　　　　　　　 D．等腰梯形

解析：由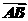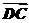＝知四边形ABCD为平行四边形，

又因为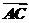·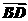＝0，即▱ABCD的两条对角线垂直，

所以四边形ABCD为菱形．

答案：B

1．已知a＝(1，sin²x)，b＝(2，sin2x)，其中x∈(0，π)．若|a·b|＝|a||b|，则tanx的值等于(　)

A．1　　　　　B．－1

C. 　　　　　　　　　　　　　　　　 　D.

解析：由|a·b|＝|a||b|知，a∥b.

所以sin2x＝2sin²x，

即2sinxcosx＝2sin²x，而x∈(0，π)，所以sinx＝cosx，

即x＝，故tanx＝1.

答案：A

8．已知复数z₁＝3－i，z₂是复数－1+2i的共轭复数，则复数－的虚部等于________．

解析：－＝－＝－＝，其虚部为.

7．在复平面内，复数1+i与－1+3i分别对应向量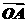和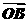，其中O为坐标原点，则| |＝________.

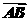解析：由题意知A(1,1)，B(－1,3)，

故|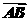|＝＝2.

答案：2

6．若M＝{x|x＝iⁿ，n∈Z}，N＝{x|＞－1}(其中i为虚数单位)，则M∩(∁_RN)＝(　)

A．{－1,1}　 　　　　　　　　　　 B．{－1}

C．{－1,0}　 　　　　　　　　　　 D．{1}

解析：依题意M＝{1，－1，i，－i}，

N＝{x|x＞0或x＜－1}，

所以∁_RN＝{x|－1≤x≤0}，故M∩(∁_RN)＝{－1}．

答案：B

5．若复数z＝cosθ+isinθ且z²+²＝1，则sin²θ＝(　)

A.　 　　　　　　　　　 B.

C.　 　　　　　　　　　 D．－

解析：z²+²＝(cosθ+isinθ)²+(cosθ－isinθ)²＝2cos2θ＝1

⇒cos2θ＝，所以sin²θ＝＝.

答案：B

4．已知复数a＝3+2i，b＝4+xi(其中i为虚数单位)，若复数∈R，则实数x的值为(　)

A．－6 　　　　　　　 　　　 B．6

C.　 　　　　　　　　　 　　　 D．－

解析：由于＝＝

＝∈R，

则8－3x＝0，∴x＝.

答案：C

3．在复平面内，向量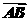对应的复数是2+i，向量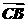对应的复数是－1－3i，则向量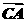对应的复数为(　)

A．1－2i　 　　　　　　　　　　　　 B．－1+2i

C．3+4i　 　　　　　　　　　　　　 D．－3－4i

解析：向量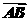对应的复数是2+i，

则对应的复数为－2－i，

∵＝+，

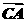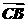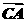∴对应的复数为(－1－3i)+(－2－i)＝－3－4i.

答案：D

2．设复数ω＝－+i，则化简复数的结果是(　)

A．－－i　 　　　　　　　　　 B．－+i

C.+i　 　　　　　　　　　　　　 D.－i

解析：∵ω²＝²＝－－i＝－－i，

∴＝＝－+i.

答案：B