
题目列表(包括答案和解析)
3.在△ABC中,若2cosBsinA=sinC,则△ABC的形状一定是( )
A.等腰直角三角形 B.直角三角形 C.等腰三角形 D.等边三角形
解析:2sinAcosB=sin(A+B)+sin(A-B)又∵2sinAcosB=sinC,
∴sin(A-B)=0,∴A=B
2.若在△ABC中,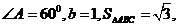 求△ABC外接圆的半径R.
求△ABC外接圆的半径R.
解析: 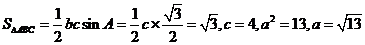
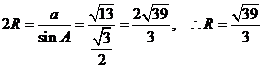
题型2判断三角形形状
[例3]在△ABC中,bcosA=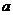 cosB,试判断三角形的形状.
cosB,试判断三角形的形状.
[解题思路]判定三角形形状时,一般考虑两个方向进行变形:(1)一个方向是边,走代数变形之路,通常是正、余弦定理结合使用;(2)另一个方向是角,走三角变形之路.通常是运用正弦定理
[解析]:方法1:利用余弦定理将角化为边.
∵bcosA=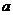 cosB ∴
cosB ∴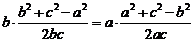
∴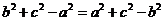 ∴
∴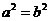 ∴
∴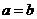
故此三角形是等腰三角形.
方法2:利用正弦定理将边转化为角.
∵bcosA=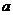 cosB 又b=2RsinB,
cosB 又b=2RsinB,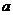 =2RsinA
=2RsinA
∴2RsinBcosA=2RsinAcosB ∴sinAcosB-cosAsinB=0
∴sin(A-B)=0 ∵0<A,B<π,∴-π<A-B<π
∴A-B=0,即A=B故三角形是等腰三角形.
[名师指引]判断三角形形状时一般从角入手,利用三角形内角和定理,实施关于三角形内角的一些变形公式.
[新题导练]
1.在△ABC中,a=1,b=,B=60°,求c.
解析:由余弦定理得 ()2=12+c2-2ccos60°,
∴c2-c-6=0,
解得c1=3,c2=-2(舍去).∴c=3.
3.重难点:通过正弦定理和余弦定理将已知条件中的角化为边或边化为角后,再实施三角变换的转化过程以及解三角形中的分类讨论问题.
(1) 已知两边和其中一对角,.求另一边的对角时要注意分类讨论
问题1: 在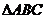 中,A、B的对边分别是
中,A、B的对边分别是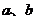 ,且
,且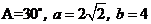 ,那么满足条件的
,那么满足条件的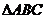 ( )
( )
A、 有一个解 B、有两个解 C、无解 D、不能确定
点拨:在解三角形中涉及到对边对角问题一般用正弦定理,由正弦值定角的原则是大边对大角。由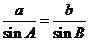 得
得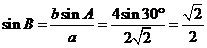 ,又
,又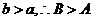 故有两解
故有两解
答案B.
在解三角形时要注意充分利用平面几何的性质
问题2: 已知圆内接四边形ABCD的边长分别为AB=2,BC=6,CD=DA=4,求四边形ABCD的面积
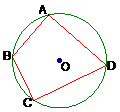 点拨 :如图连结BD,则有四边形ABCD的面积
点拨 :如图连结BD,则有四边形ABCD的面积
S=S△ABD+S△CDB=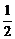 ·AB·ADsinA+
·AB·ADsinA+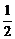 ·BC·CD·sinC
·BC·CD·sinC
∵A+C=180°,∴sinA=sinC
故S=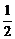 (AB·AD+BC·CD)sinA=
(AB·AD+BC·CD)sinA=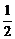 (2×4+6×4)sinA=16sinA
(2×4+6×4)sinA=16sinA
由余弦定理,在△ABD中,BD2=AB2+AD2-2AB·AD·cosA=20-16cosA
在△CDB中,BD2=CB2+CD2-2CB·CD·cosC=52-48cosC
∴20-16cosA=52-48cosC,∵cosC=-cosA,
∴64cosA=-32,cosA=-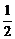 ,
,
又0°<A<180°,∴A=120°故S=16sin120°=8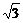

★ 热 点 考 点 题 型 探 析★
考点1: 运用正、余弦定理求角或边
题型1.求三角形中的某些元素
[例1] (2008年广州市海珠区高三上期综练二)已知:A、B、C是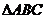 的内角,
的内角,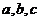 分别是其对边长,向量
分别是其对边长,向量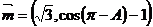 ,
,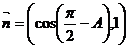 ,
,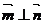 .
.
(Ⅰ)求角A的大小;
(Ⅱ)若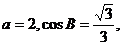 求
求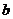 的长.
的长.
[解题思路]已知对边求对角,直接用正弦定理。
解析:(Ⅰ) 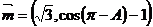 =
=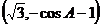 ……1分
……1分
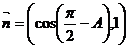 =
=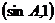 ……2分
……2分
∵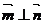
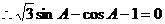 ……4分
……4分
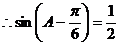 ……6分
……6分
∵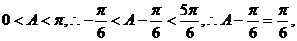 ……7分
……7分
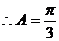 .……8分
.……8分
(Ⅱ)在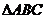 中,
中,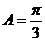 ,
,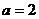 ,
,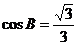
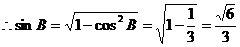 ……9分
……9分
由正弦定理知: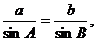 ……10分
……10分
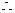
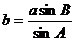 =
=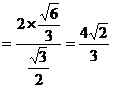 .
.
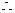
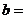
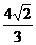 ……12分
……12分
[名师指引]已知两边和其中一边的对角(如a、b、A),应用正弦定理求B,由A+B+C = π求C,要注意解可能有多种情况
[新题导练]
2.难点:根据已知条件,确定边角转换.
1.重点:熟练掌握正弦定理、余弦定理和面积公式,利用内角和定理实现三内角之间的转换,解题时应注意四大定理的正用、逆用和变形用
4.余弦定理:三角形任何一边的平方等于其他两边的平方的和减去这两边与它们夹角的余弦的积的两倍..
形式一: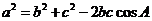
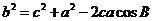 (解三角形的重要工具)
(解三角形的重要工具)
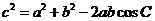
形式二: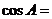
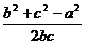 ;
; 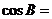
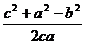 ; cosC=
; cosC=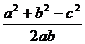
★ 重 难 点 突 破 ★
3.正弦定理:在一个三角形中,各边和它的所对角的正弦的比相等.
形式一: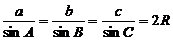 (解三角形的重要工具)
(解三角形的重要工具)
形式二: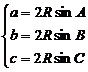 (边角转化的重要工具)
(边角转化的重要工具)
10. 12.用二分法求方程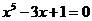 在
在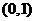 上的近似解,精确到
上的近似解,精确到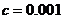 ,写出算法.画出流程图,并写出算法语句.
,写出算法.画出流程图,并写出算法语句.
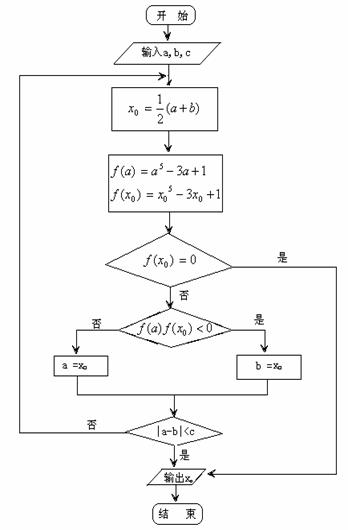
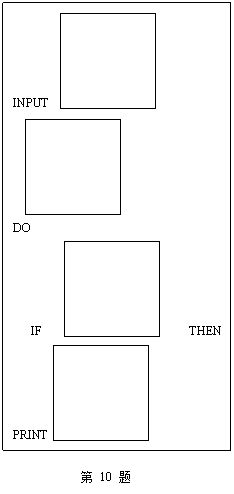 [解析]算法如下:
[解析]算法如下:
第一步:取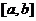 中点
中点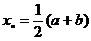 ,将区间一分为二;
,将区间一分为二;
第二步:若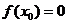 ,则
,则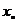 就是方程的根;
就是方程的根;
否则所求根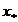 在
在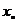 的左侧或右侧;
的左侧或右侧;
若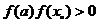 ,则
,则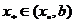 ,以
,以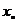 代替
代替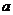 ;
;
若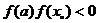 ,则
,则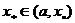 ,以
,以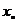 代替
代替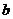 ;
;
第三步:若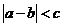 ,计算终止 此时
,计算终止 此时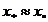 ,
,
否则转到第一步.
算法语句和流程图如图所示:
9.给出以下四个问题:
①输入一个数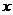 , 输出它的相反数;②求面积为
, 输出它的相反数;②求面积为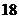 的正方形的周长;③求三个数
的正方形的周长;③求三个数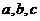 中的最大数;
中的最大数;
④求函数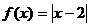 的函数值. 其中不需要用条件语句来描述其算法的有
的函数值. 其中不需要用条件语句来描述其算法的有
[解析]②.仅②不需要分情况讨论,即不需要用条件语句.
综合拔高训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com