1．直线l：ax+y－2－a＝0在x轴和y轴上的截距相等，则a的值是(　)

A．1　 　　　　　　　　　　　　　　　　　　　 B．－1

C．－2或－1　 　　　　　　　　　　　　 D．－2或1

解析：由a+2＝，∴a＝－2或1.

答案：D

12．已知向量m＝(sin，1)，n＝(cos，cos²)．

(1)若m·n＝1，求cos(－x)的值；

(2)记f(x)＝m·n，在△ABC中，角A，B，C的对边分别是a，b，c，且满足(2a－c)cosB＝bcosC，求函数f(A)的取值范围．

解：(1)∵m·n＝1，即sincos+cos²＝1，

即sin+cos+＝1，

∴sin(+)＝.

∴cos(－x)＝cos(x－)＝－cos(x+)

＝－[1－2sin²(+)]

＝2·()²－1＝－.

(2)∵(2a－c)cosB＝bcosC，

由正弦定理得(2sinA－sinC)cosB＝sinBcosC.

∴2sinAcosB－cosBsinC＝sinBcosC，

∴2sinAcosB＝sin(B+C)，

∵A+B+C＝π，

∴sin(B+C)＝sinA，且sinA≠0，

∴cosB＝，B＝，∴0＜A＜.

∴＜+＜，＜sin(+)＜1.

又∵f(x)＝m·n＝sin(+)+，

∴f(A)＝sin(+)+.

故函数f(A)的取值范围是(1，)．

11．设在平面上有两个向量a＝(cosα，sinα)(0°≤α<360°)，b＝(－，)．

(1)求证：向量a+b与a－b垂直；

(2)当向量a+b与a－b的模相等时，求α的大小．

解：(1)证明：因为(a+b)·(a－b)＝|a|²－|b|²＝(cos²α+sin²α)－(+)＝0，

故a+b与a－b垂直．

(2)由|a+b|＝|a－b|，两边平方得

3|a|²+2a·b+|b|²＝|a|²－2a·b+3|b|²，

所以2(|a|²－|b|²)+4a·b＝0，

而|a|＝|b|，所以a·b＝0，

则(－)×cosα+×sinα＝0，即cos(α+60°)＝0，

∴α+60°＝k·180°+90°，即α＝k·180°+30°，k∈Z，

又0°≤α＜360°，则α＝30°或α＝210°.

10．已知向量a＝(1,2)，b＝(2，－2)．

(1)设c＝4a+b，求(b·c)a；

(2)若a+λb与a垂直，求λ的值；

(3)求向量a在b方向上的投影．

解：(1)∵a＝(1,2)，b＝(2，－2)，

∴c＝4a+b＝(4,8)+(2，－2)＝(6,6)．

∴b·c＝2×6－2×6＝0，∴(b·c)a＝0a＝0.

(2)a+λb＝(1,2)+λ(2，－2)＝(2λ+1,2－2λ)，

由于a+λb与a垂直，

∴2λ+1+2(2－2λ)＝0，∴λ＝.

(3)设向量a与b的夹角为θ，

向量a在b方向上的投影为|a|cosθ.

∴|a|cosθ＝＝＝－＝－.

9．给出以下四个命题：

①对任意两个向量a，b都有|a·b|＝|a||b|；

②若a，b是两个不共线的向量，且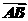＝λ₁a+b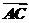，＝a+λ₂b(λ₁，λ₂∈R)，则A、B、C共线⇔λ₁λ₂＝－1；

③若向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，则a+b与a－b的夹角为90°.

④若向量a、b满足|a|＝3，|b|＝4，|a+b|＝，则a，b的夹角为60°.

以上命题中，错误命题的序号是________．

解析：①错，∵|a·b|＝|a||b|·|cosθ|≤|a||b|.

②错．∵A、B、C共线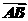，∴＝k，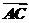

∴∴λ₁λ₂＝1.

④错，∵|a+b|²＝13，

∴|a|²+|b|²+2a·b＝13，

即a·b＝|a||b|·cosθ＝－6，

∴cosθ＝－，∴θ＝120°.

答案：①②④

8．已知向量a＝(2，－1)，b＝(x，－2)，c＝(3，y)，若a∥b，(a+b)⊥(b－c)，M(x，y)，N(y，x)，则向量的模为________．

解析：∵a∥b，∴x＝4，∴b＝(4，－2)，

∴a+b＝(6，－3)，b－c＝(1，－2－y)．∵(a+b)⊥(b－c)，

∴(a+b)·(b－c)＝0，即6－3×(－2－y)＝0，∴y＝－4，

∴M(4，－4)，N(－4,4)．

故向量＝(－8,8)，||＝8.

答案：8

7．力F的大小为50 N，与水平方向的夹角为30°(斜向上)，使物体沿水平方向运动了20 m，则力F所做的功为________．

解析：设木块的位移为s，

则F·s＝|F|·|s|cos30°＝50×20×＝500(J)．

答案：500 J

6．若△ABC的三个内角A，B，C成等差数列，且(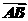+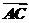)·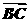＝0，则△ABC一定是(　)

A．等腰直角三角形　 　　　　　　　　　　 B．非等腰直角三角形

C．等边三角形　 　　　　　　　　　　　　　　 D．钝角三角形

解析：由题意可知，在△ABC中，BC边上的中线又是BC边上的高，因此△ABC是等腰三角形，而三个内角A，B，C成等差数列，故角B为60°，所以△ABC一定是等边三角形．

答案：C

5．设向量a＝(cosα，sinα)，b＝(cosβ，sinβ)，其中0<α<β<π，若|2a+b|＝|a－2b|，则β－α＝(　)

A.　 　　　　　　　　　 B．－

C.　 　　　　　　　　　 D．－

解析：由|2a+b|＝|a－2b|得3|a|²－3|b|²+8a·b＝0，

而|a|＝|b|＝1，故a·b＝0，

∴cosαcosβ+sinαsinβ＝0，

即cos(α－β)＝0，由于0<α<β<π，

故－π<α－β<0，∴α－β＝－，即β－α＝.

答案：A

4．在锐角△ABC中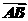，＝a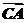，＝b，S_△ABC＝1，且|a|＝2，|b|＝，则a·b等于(　)

A．－2　 　　　　　　　　　　 B．2

C．－　 　　　　　　　　　　 D.

解析：S_△ABC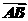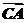＝||||sinA＝×2×sinA＝1，

∴sinA＝，

∵A为锐角，∴A＝.

∴a·b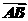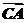＝·＝|a||b|cos(π－A)

＝2×cos＝－2.

答案：A