
题目列表(包括答案和解析)
1. 已知集合
已知集合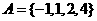 ,
,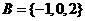 ,则
,则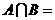 ▲
.
▲
.
(11)设f(x)是定义R上的奇函数,当x≤ 0时,f(x)=2x2-x,f(1)=___________
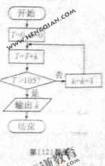
(12)如图所示,程序框图(算法流程图)的输出结果是___________
(13)函数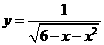 的定义域是___________
的定义域是___________
(14)已知向量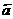 ,
,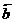 满足(
满足(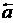 +2
+2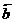 ) • (
) • (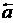 -
-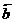 ),|
),|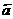 |=1,|
|=1,|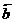 |=2则
|=2则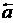 与
与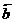 的夹角为___________
的夹角为___________
(15)设 若
若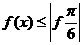 对一切
对一切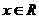 恒成立,则
恒成立,则
①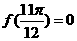
②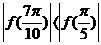
③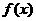 既不是奇函数也不是偶函数
既不是奇函数也不是偶函数
④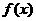 的单调递增区间是
的单调递增区间是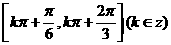
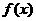 过点(a,b)的直线相交
过点(a,b)的直线相交
以上结论正确的是_____________________________(写出正确结论的编号)
(1)设i是虚数单位,复数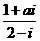 为纯复数,则是数
为纯复数,则是数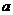 为
为
(A)
2
(B) -2
(C) -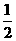 (D)
(D) 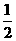
(2)集合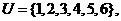
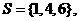
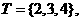 则
则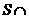 ()等于
()等于
(A)
(B) 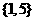
(C) 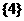 (
D)
(
D) 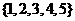
(3) 油长是
(A)2 (B) 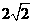 (C)4
(D)
(C)4
(D) 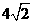
(4)若直线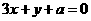 过圆
过圆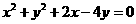 的圆心,则
的圆心,则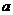 的值为
的值为
(A)-1 (B) 1 (C)3 (D)-3
(5)若点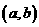 在
在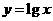 图像上,
图像上,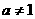 ,则下列点也在此图像上的是
,则下列点也在此图像上的是
(A)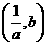 (B)
(B)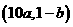 (C)
(C)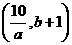 (D)
(D)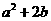
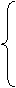 (6)设变量
(6)设变量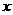 ,
,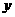 满足
满足 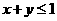 则
则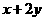 的最大值和最小值分别为
的最大值和最小值分别为
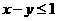
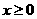
(A)1,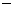 1
(B)2,
1
(B)2, 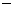 2
(C)1,
2
(C)1, 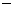 2
(D)2,
2
(D)2,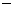 1
1
(7)若数列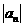 的通项公式是
的通项公式是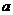 n=(-1)n(3
n=(-1)n(3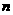 -2),则
-2),则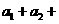 …
…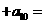
(A)15
(B)12
(C)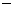 12
(D)
12
(D) 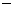 15
15
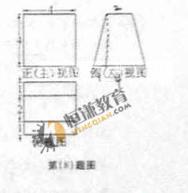 (8)一个空间几何体的三视图如图所示,则该几何体的表面积为
(8)一个空间几何体的三视图如图所示,则该几何体的表面积为
(A)48 (B)32+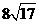 (C)48+
(C)48+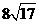 (D)80
(D)80
(9)从六边形的6个顶点中随机选择4个顶点,则以它们作为顶点的四边形是矩形的概率等于
(A)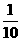 (B)
(B)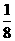
(C)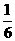 (D)
(D)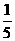
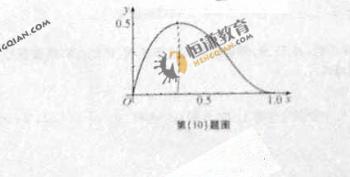
(10)函数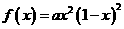 在区间
在区间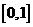 上的图像如图所示,则
上的图像如图所示,则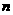 可能是
可能是
(A)1 (B)2 (C)3 (D)4
2011年普通高等学校招生全国统一考试(安徽卷)
数学(文科)
第 Ⅱ卷 (非选择题 共100分)
请用0.5毫米黑色墨水签字笔答题,在试题卷上答题无效
(16)(本小题满分12分)
**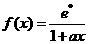
 ,其中
,其中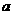 为正实数
为正实数
(Ⅰ)当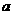
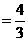 时,求
时,求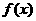 的极值点;
的极值点;
(Ⅱ)若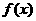 为
为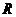 上的单调函数,求
上的单调函数,求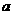 的取值范围。
的取值范围。
(17)(本小题满分12分)
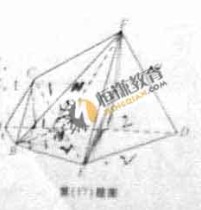
如图,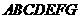 为多面体,平面
为多面体,平面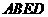 与平面
与平面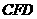 垂直,点
垂直,点 在线段
在线段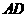 上,
上,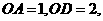 △
△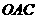 ,△
,△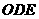 ,△
,△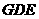 都是正三角形。
都是正三角形。
(Ⅰ)证明直线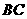 ∥
∥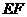 ;
;
(Ⅱ)求梭锥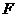 -
-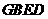 的体积。
的体积。
(18)(本小题满分13分)
在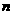 +2数列中,加入
+2数列中,加入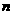 个实数,使得这
个实数,使得这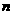 +2个数构成递增的等比数列,将这
+2个数构成递增的等比数列,将这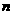 +2个数,令
+2个数,令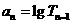 ,
,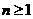
(Ⅰ)求数列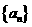 的等项公式;
的等项公式;
(Ⅱ)设求数列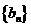 的前
的前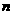 项和
项和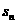 .
.
(19)(本小题满分12分)
(Ⅰ)设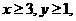 证明
证明
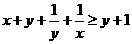
(Ⅱ)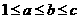 ,证明
,证明
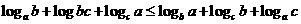
(20)(本小题满分13分)
工作人员需进入核电站完成某项具有高辐射危险的任务,每次只派一个人进去,且每个人只需一次,工作时间不超过10分钟,如果有一个人10分钟内不能完成任务则撤出,再派下一个人。现在一共只有甲、乙、丙一个人可派,他们各自能完成任务的概率分别p1,p2,p3,假设p1,p2,p3,互相相等,且规定各人能否完成任务的事件相互独立.
(Ⅰ)如果按甲在先,乙次之,丙最后的顺序派人,球任务能被完成的概率。若改变三个人被派出的先后顺序,任务能被完成的概率是否发生变化?
(Ⅱ)若按某指定顺序派人,这三个人各自能完成任务的概率依次为q1,q2,q3,其中q1,q2,q3是p1,p2,p3的一个排列,求所需要派出人员数目X的分布列和均值(数字期望)EX;
(Ⅲ)假定l>p1>p2>p3,试分析以怎样的先后顺序派出人员,可使所需派出的人员数目的均值(数字期望)达到最小。
(21)(本小题满分13分)
若A=0,点A的坐标为(1,1),点B在抛物线y=x上运动,点Q满足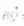 =
=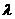
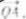 ,经过点Q与x轴垂直的直线交抛物线于点M,点P满足
,经过点Q与x轴垂直的直线交抛物线于点M,点P满足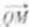 =
=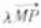 ,求点P的轨迹方程。
,求点P的轨迹方程。
(11)如图所示,程序框图(算法流程图)的输出结果是____________
(12)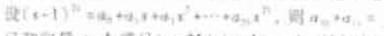 ________________
________________
(13)已知向量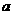 、
、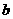 满足
满足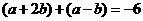 ,且
,且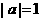 ,
,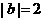 ,则
,则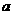 与
与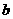 的夹角为_____________________
的夹角为_____________________
(14)已知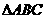 的一个内角为120o,并且三边长构成公差为4的等差数列,则
的一个内角为120o,并且三边长构成公差为4的等差数列,则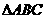 的面积为_______________
的面积为_______________
(15)在平面直角坐标系中,如果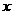 与???就称点
与???就称点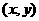 ??题中正确的是_____________(写出所有正确命题的编号).
??题中正确的是_____________(写出所有正确命题的编号).
①存在这样的直线,既不与坐标轴平行又不经过任何整点
②如果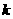 与
与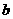 都是无理数,则直线
都是无理数,则直线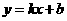 不经过任何整点
不经过任何整点
③直线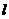 经过无穷多个整点,当且仅当
经过无穷多个整点,当且仅当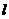 经过两个不同的整点
经过两个不同的整点
④直线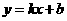 经过无穷多个整点的充分必要条件是:
经过无穷多个整点的充分必要条件是: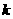 与
与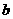 都是有理数
都是有理数
⑤存在恰经过一个整点的直线
(1)设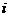 是虚数单位,复数
是虚数单位,复数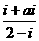 为纯虚数,则实数a为
为纯虚数,则实数a为
(A)2
(B)-2 (C)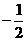 (D)
(D)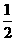
(2)双曲线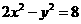 的实轴长是
的实轴长是
(A)2 (B)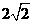 (C)4 (D)
(C)4 (D)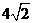
(3)设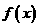 是定义在R上的奇函数,当
是定义在R上的奇函数,当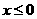 时,
时,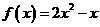 ,则
,则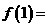
(A)-3 (B)-1 (C)1 (D)3
(4)设变量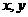 满足
满足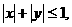 则
则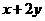 的最大值和最小值分别为
的最大值和最小值分别为
(A)1,-1 (B)2,-2 (C)1,-2 (D)2,-1
(5) 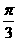 到圆
到圆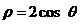 的圆心的距离为
的圆心的距离为
(A)2
(B) 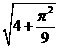 (C)
(C)
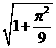 (D)
(D) 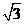
(6)一个空间几何体得三视图如图所示,则该几何体的表面积为
(A)48 
(B)32+8,17
(C)48+8,17
(D)50
(7)命题“所有能被2整除的数都是偶数”的否定是
(A)所有不能被2整除的数都是偶数
(B)所有能被2整除的数都不是偶数
(C)存在一个不能被2整除的数都是偶数
(D)存在一个不能被2整除的数都不是偶数
(8)设集合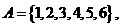
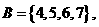 则满足
则满足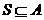 且
且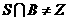 的集合
的集合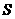 为
为
(A)57 (B)56 (C)49 (D)8
(9)已知函数 为实数,若
为实数,若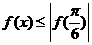 对
对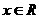 恒成立,
恒成立,
且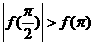 ,则
,则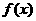 的单调递增区间是
的单调递增区间是
(A)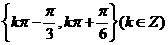 (B)
(B)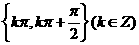
(C)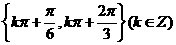 (D)
(D)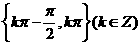
(10)函数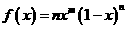 在区间
在区间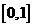 上的图像如图所示,则
上的图像如图所示,则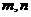 得知可能是
得知可能是
(A)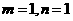 (B)
(B) 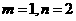
(C) 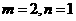 (D)
(D)
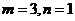
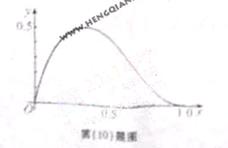
第Ⅱ卷 (非选择题 共100分)
请用0.5毫米黑色墨水签字笔在答题卡上作答,在试题卷上答题无效。
(17)(本小题满分10分)(注意:在试题卷上作答无效)
△ ABC的内角A、B、C的对边分别为a、b、c.已知A-C=90°,a+c=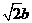 ,求C.
,求C.
(18)(本小题满分12分)(注意:在试题卷上作答无效)
根据以往统计资料,某地车主购买甲种保险的概率为0.5,购买乙种保险但不购买甲种保险的概率为0.3.设各车主购买保险相互独立.
(Ⅰ)求该地1位车主至少购买甲、乙两种保险中的1种概率;
(Ⅱ)X表示该地的100位车主中,甲、乙两种保险都不购买的车主数.求X的期望.
(19)(本小题满分12分)(注意:在试题卷上作答无效)
如图,棱锥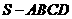 中,
中,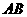 ∥
∥ ,
,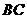 ⊥
⊥ ,侧面
,侧面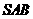 为等边三角形,
为等边三角形,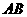 =
=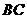 =2,
=2, =
=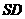 =1。
=1。
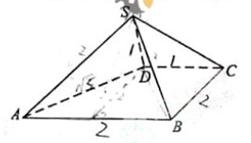 (I)证明:
(I)证明: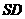 ⊥平面
⊥平面 ;
;
(II)求 与平面
与平面 所成的角的大小。
所成的角的大小。
(20)(本小题满分12分)(注意:在试题卷上作答无效)
设数列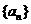 满足
满足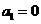 且
且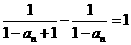 。
。
(I)求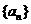 的通项公式;
的通项公式;
(II)设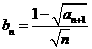 ,记
,记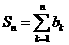 ,证明:
,证明: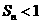 。
。
 (21)(本小题满分12分)(注意:在试题卷上答无效)
(21)(本小题满分12分)(注意:在试题卷上答无效)
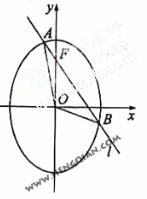
已知O为坐标原点,F为椭圆C: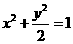 在
在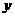 轴正半轴上的焦点,过F且斜率为-
轴正半轴上的焦点,过F且斜率为-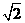 的直线
的直线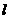 与C交于A、B两点,点P满足
与C交于A、B两点,点P满足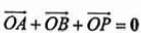 .
.
(Ⅰ)证明:点P在C上;
(Ⅱ)设点P关于点O的对称点为Q,证明:A、P、B、Q四点在同一圆上。
(22)(本小题满分12分)(注意:在试题卷上答无效)
(Ⅰ)设函数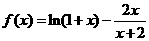 ,证明:当
,证明:当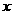 >0时,
>0时,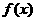 >0;
>0;
(Ⅱ)从编号1到100的100张卡片中每次随机抽取一张,然后放回,用这种方式连续抽取20次,设抽得的20个号码互补相同的概率为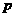 .证明:
.证明: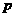 <(
<(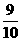 )19<
)19<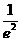 .
.
(13)(1-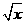 )20的二项展开式中,x 的系数与x9的系数之差为____________________.
)20的二项展开式中,x 的系数与x9的系数之差为____________________.
(14)已知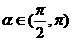 ,sin
,sin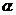 =
=
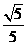 ,则tan2
,则tan2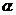 =______________
=______________
(15)已知F1、F2分别为双曲线C: 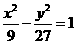 的左、右焦点,点
的左、右焦点,点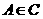 ,点M的坐标为(2,0),AM为∠F1AF2的平分线,则
,点M的坐标为(2,0),AM为∠F1AF2的平分线,则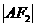 ______________
______________
(16)已知E、F分别在正方形ABCD、A1B1C1D1楞BB1,CC1上,且B1F=2EB,CF=2FC1,则面AEF与面ABC所成的二面角的正切值等于_______________。
(17)(本小题满分12分)
在 △ABC中,内角A,B,C的对边分别为a,b,c.已知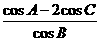 =
=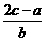 。
。
(Ⅰ)求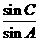 的值;
的值;
(Ⅱ)若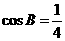 , △ABC的周长为5,求b的长。
, △ABC的周长为5,求b的长。
(18)(本小题满分12分)
甲、乙两校各有3名教师报名支教,其中甲校2男1女,乙校1男2女。
(Ⅰ)若从甲校和乙校报名的教师中各任选1名,写出所有可能的结果,并求选出的2名教师性别相同的概率;
(Ⅱ)若从报名的6名教师中任选2名,写出所有可能的结果,并求选出的2名教师来自同一学校的概率。
(19)(本小题满分12分)
如图,在四棱台ABCD-A1B2C3D4中,D1D⊥平面ABCD是平行四边形,AB=2AD,AD=A1B1, ∠ BAD= ,
,
(Ⅰ)证明:AA1⊥ BD;
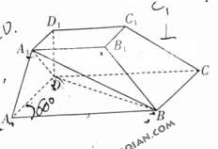
(Ⅱ)证明:CC1∥ABD
(20)(本小题满分12分)
数列﹛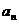 ﹜中
﹜中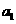 、
、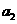 、
、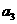 分别是下表第一、二、三行中的某一个数,且
分别是下表第一、二、三行中的某一个数,且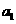 、
、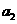 、
、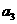 中的任何两个数不在下表的同一列.
中的任何两个数不在下表的同一列.
|
|
第一列 |
第二列 |
第三列 |
|
第一行 |
3 |
2 |
10 |
|
第二行 |
6 |
4 |
14 |
|
第三行 |
9 |
8 |
18 |
(Ⅰ)求数列﹛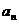 ﹜的通项公式;
﹜的通项公式;
(Ⅱ)若数列﹛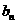 ﹜满足:
﹜满足: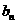 =
=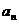 +
+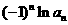 ,求数列﹛
,求数列﹛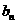 ﹜的前2
﹜的前2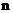 项和
项和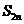 .
.
(21)(本小题满分12分)
 某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端为半球形,按照设计要求容器的容积为
某企业拟建造如图所示的容器(不计厚度,长度单位:米),其中容器的中间为圆柱形,左右两端为半球形,按照设计要求容器的容积为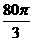 立方米,且
立方米,且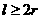 ,假设该容器的建造费用仅与其表面积有关。已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米费用为
,假设该容器的建造费用仅与其表面积有关。已知圆柱形部分每平方米建造费用为3千元,半球形部分每平方米费用为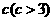 千元。设该容器的建造费用为
千元。设该容器的建造费用为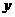 千元。
千元。
(I)写出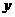 关于
关于 的函数表达式,并求该函数的定义域;
的函数表达式,并求该函数的定义域;
(II)求该容器的建造费用最小时的 。
。
(22)(本小题满分14分)
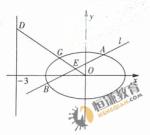 在平面直角坐标系xOy中,已知椭圆C:
在平面直角坐标系xOy中,已知椭圆C: 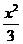 +
+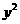 =1.如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于A,B两点,线段AB的中点为E,射线OE交椭圆C于点C,交直线x=-3于点D(-3,m).
=1.如图所示,斜率为k(k>0)且不过原点的直线l交椭圆C于A,B两点,线段AB的中点为E,射线OE交椭圆C于点C,交直线x=-3于点D(-3,m).
(Ⅰ)求m2+k2的最小值;
(Ⅱ)若 2=
2=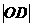 •
•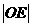 ,
,
(i)求证:直线l过定点;
(ii)试问点B,G能否关于x轴对称?若能,求出此时△ABG的外接圆方程;若不能,请说明理由。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com