
题目列表(包括答案和解析)
2.我们知道,函数 的图象经过适当变换可以得到
的图象经过适当变换可以得到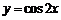 的图象,则这种变换可以是
的图象,则这种变换可以是
A.沿x轴向右平移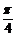 个单位 B.沿x轴向左平移
个单位 B.沿x轴向左平移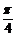 个单位
个单位
C.沿x轴向左平移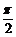 个单位 D.沿x轴向右平移
个单位 D.沿x轴向右平移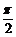 个单位
个单位
解析: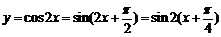 选B
选B
考点2 确定函数解析式问题
题型1:分析图形定参数
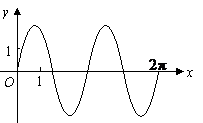 例1.(08海南、宁夏省) 已知函数
例1.(08海南、宁夏省) 已知函数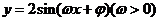 )在区间
)在区间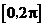 的图像如下:那么
的图像如下:那么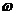 =( )
=( )
A.1 B.2
C.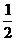 D.
D.
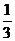
[解题思路]在解析式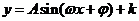 中
中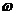 的值由周期确定,从图象分析周期为
的值由周期确定,从图象分析周期为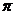
[解析]由图象知函数的周期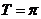 ,所以
,所以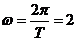
答案:B
[名师指引]确定函数 的解析式就是确定其中的参数
的解析式就是确定其中的参数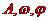 等,从图像的特征上寻找答案,它的一般步骤是:
等,从图像的特征上寻找答案,它的一般步骤是: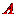 主要由最值确定,
主要由最值确定, 是由周期确定,周期通过特殊点观察求得,
是由周期确定,周期通过特殊点观察求得,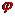 可由点在函数图像上求得,确定
可由点在函数图像上求得,确定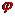 值时,注意它的不唯一性,一般要求
值时,注意它的不唯一性,一般要求 中最小的
中最小的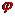 .
.
题型2.分析图象特征确定参数再求值
例2.(广东省实验中学2008学年高三第二次阶段测试试
已知向量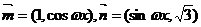 ,(
,(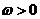 ),函数
),函数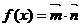 且f(x) 图像上一个最高点的坐标为
且f(x) 图像上一个最高点的坐标为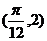 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为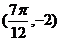 .
.
( 1 )求f(x)的解析式。
(2)在△ABC中,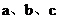 是角
是角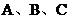 所对的边,且满足
所对的边,且满足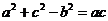 ,求角B的大小以及f(A)取值范围。
,求角B的大小以及f(A)取值范围。
[解题思路]将条件代入求参数,分析角之间的关系求值.
解析:(Ⅰ)
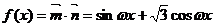 ………………………1分
………………………1分
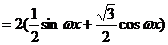 ………………………2分
………………………2分
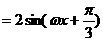 …………………………………3分
…………………………………3分
∵f(x) 图像上一个最高点的坐标为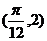 ,与之相邻的一个最低点的坐标为
,与之相邻的一个最低点的坐标为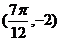 .
.
∴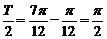 ,所以
,所以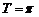 ,于是
,于是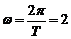 …………………4分
…………………4分
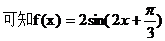 …………………………5分
…………………………5分
(2)∵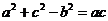 ,∴
,∴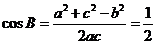 ,…………………7分
,…………………7分
又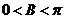 ,∴
,∴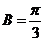 …………………8分
…………………8分
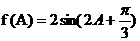 , ∵
, ∵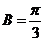 ,∴
,∴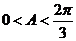 ,
,
可知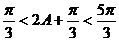 …………………10分
…………………10分
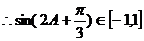
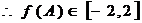 …………………12分
…………………12分
[名师指引].按确定 的解析式的一般步骤定参数.
的解析式的一般步骤定参数.
题型3. 分析图表确定参数再研究函数的性质
例3. 已知函数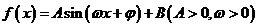 的一系列对应值如下表:
的一系列对应值如下表:
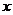
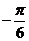
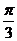
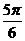
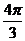
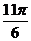
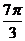
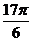
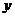
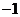
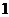
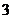
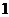
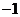
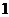
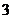
(1)根据表格提供的数据求函数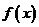 的一个解析式;
的一个解析式;
(2)根据(1)的结果,若函数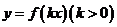 周期为
周期为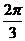 ,当
,当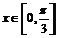 时,方程
时,方程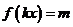 恰有两个不同的解,求实数
恰有两个不同的解,求实数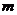 的取值范围;
的取值范围;
[解题思路]分析图表发现周期性、最值、对称点坐标确定参数.借助数形结合讨论方程的解.
解:(1)设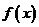 的最小正周期为
的最小正周期为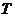 ,得
,得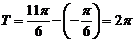 …………………….. 2分
…………………….. 2分
 由
由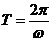 得
得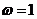
又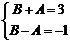 ,解得
,解得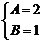 …………………….. 3分
…………………….. 3分
令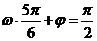 ,即
,即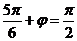 ,解得
,解得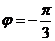
∴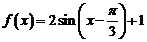 ……………………..
5分
……………………..
5分
(2)∵函数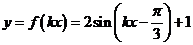 的周期为
的周期为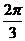
又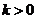 ∴
∴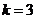 ……………………..
6分
……………………..
6分
令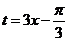 ,∵
,∵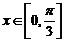 ∴
∴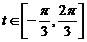 ……………………..
8分
……………………..
8分
如图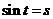 在
在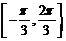 上有两个不同的解的充要条件是
上有两个不同的解的充要条件是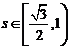
∴方程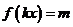 在
在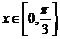 时恰好有两个不同的解的充要条件是
时恰好有两个不同的解的充要条件是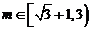 ,
,
即实数的取值范围是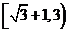 …………………….. 12分
…………………….. 12分
[名师指引]高考中三角函数的大题往往在知识的交汇处入手.
[新题导练]
1.(2008·东莞五校联考题)将函数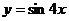 的图像向左平移
的图像向左平移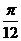 个单位,得到
个单位,得到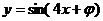 的图像,则
的图像,则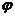 等于( )
等于( )
A、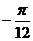 B、
B、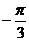 C、
C、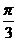 D、
D、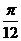
解析.C.[将函数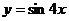 的图像向左平移
的图像向左平移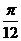 个单位,得到
个单位,得到
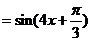 ]
]
3.重难点:合理利用三角变换公式化简三角函数解析式,分析图象特征求参数值,研究三角函数的性质以及解析一些实际问题。
(1).三角函数的性质要熟记。
问题1 (广东省五校2008年高三上期末联考)定义行列式运算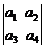 =
=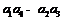 . 将函数
. 将函数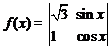 的图象向左平移
的图象向左平移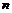 (
(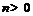 )个单位,所得图象对应的函数为偶函数,则
)个单位,所得图象对应的函数为偶函数,则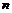 的最小值为
的最小值为
A.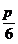 B.
B.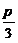 C.
C.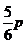 D.
D.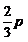
点拨:本题考查了信息的处理、迁移和应用能力以及三角函数的基础知识.

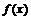 =2cos(x+
=2cos(x+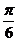 ) 左移 n 2cos(x+n+
) 左移 n 2cos(x+n+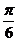 )
, 因此,n=
)
, 因此,n=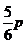 选C
选C
(2)对三角函数图像的对称性和平移变换要熟练掌握
问题2. (潮州市2008~2009学年度第一学期高三级期末质量检测)
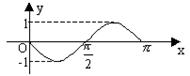 已知函数
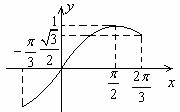
已知函数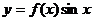 的一部分图象如右图所示,则函数
的一部分图象如右图所示,则函数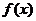 可以是
可以是
A 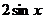 B
B 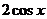
C 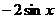 D
D
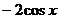
点拨:用代入法,结合周期为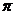 及对称性可知选D
及对称性可知选D
(3)重视三角函数的应用题
问题3. 某港口水的深度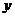 (米)是时间
(米)是时间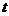 (
(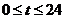 ,单位:时)的函数,记作
,单位:时)的函数,记作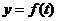 , 下面是某日水深的数据:
, 下面是某日水深的数据:
|
t/h |
0 |
3 |
6 |
9 |
12 |
15 |
18 |
21 |
24 |
|
y/m |
10.0 |
13.0 |
9.9 |
7.0 |
10.0 |
13.0 |
10.1 |
7.0 |
10.0 |
经常期观察,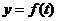 的曲线可以近似的看成函数
的曲线可以近似的看成函数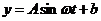 的图象,根据以上的数据,可得函数
的图象,根据以上的数据,可得函数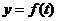 的近似表达式为
.
的近似表达式为
.
解析:从表可以看出,当t=0时,y=10,且函数的最小正周期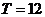
 ∴b=10,由
∴b=10,由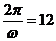 得
得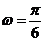 ,由
,由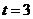 时
时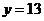 得
得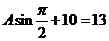 ∴
∴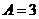 ,∴
,∴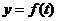 的近似表达式为
的近似表达式为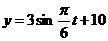 ,
,
★热 点 考 点 题 型 探 析
考点1 函数图象变换问题
题型:将几何条件转化为参数的值.
[例1](2008·广东省惠州市高三第二次调研考试 )将函数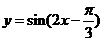 的图象先向左平移
的图象先向左平移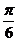 ,然后将所得图象上所有点的横坐标变为原来的
,然后将所得图象上所有点的横坐标变为原来的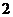 倍(纵坐标不变),则所得到的图象对应的函数解析式为( ).
倍(纵坐标不变),则所得到的图象对应的函数解析式为( ).
A.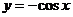 B.
B.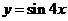 C.
C.  D.
D.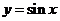
[解题思路]直接按变换法则进行转化
[解析]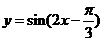 的图象先向左平移
的图象先向左平移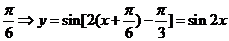 ,横坐标变为原来的
,横坐标变为原来的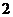 倍
倍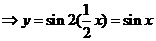 .选
.选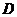 .
.
[名师指引]三角函数图象变换问题一般步骤是先平移再伸缩.
[新题导练]
2.难点:将三角函数式化为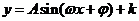 的过程以及已知
的过程以及已知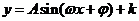 的图象求参数
的图象求参数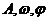 的过程
的过程
1.重点:熟练掌握平移、伸缩、振幅等变换法则处理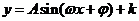 与
与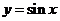 图象间的关系
图象间的关系
10. (汕头金山中学09届高三11月考)在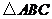 中,内角
中,内角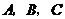 对边的边长分别是
对边的边长分别是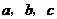 ,已知
,已知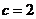 ,
,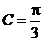 .
.
(Ⅰ)若 的面积等于
的面积等于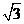 ,求
,求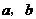 ;
;
(Ⅱ)若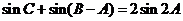 ,求
,求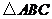 的面积.
的面积.
解:(Ⅰ)由余弦定理及已知条件得,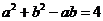 ,
,
又因为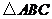 的面积等于
的面积等于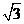 ,所以
,所以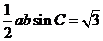 ,得
,得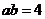 .
.
联立方程组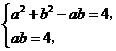 解得
解得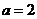 ,
,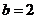 .
.
(Ⅱ)由题意得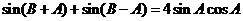 ,
,
即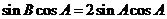 ,当
,当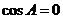 时,
时,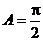 ,
,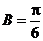 ,
,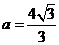 ,
,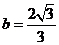 ,
,
当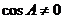 时,得
时,得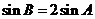 ,由正弦定理得
,由正弦定理得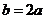 ,
,
联立方程组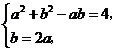 解得
解得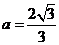 ,
,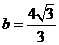 .
.
所以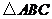 的面积
的面积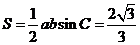 .
.
9. 在△ABC中,若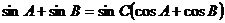 .
.
(1)判断△ABC的形状;
(2)在上述△ABC中,若角C的对边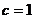 ,求该三角形内切圆半径的取值范围。
,求该三角形内切圆半径的取值范围。
解:(1)由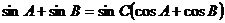
可得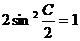
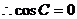 即C=90°
即C=90°
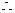 △ABC是以C为直角顶点得直角三角形
△ABC是以C为直角顶点得直角三角形
(2)内切圆半径
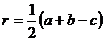
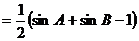
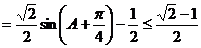
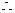 内切圆半径的取值范围是
内切圆半径的取值范围是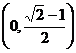
8.在锐角三角形中,边a、b是方程x2-2x+2=0的两根,角A、B满足:
2sin(A+B)-=0,求△ABC的面积。
解:由2sin(A+B)-=0,得sin(A+B)=, ∵△ABC为锐角三角形
∴A+B=120°, C=60°, 又∵a、b是方程x2-2x+2=0的两根,∴a+b=2,
a·b=2, ∴c2=a2+b2-2a·bcosC=(a+b)2-3ab=12-6=6,
∴c=, 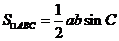 =×2×= 。
=×2×= 。
7.在△ABC中,已知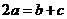 ,
,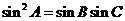 ,试判断△ABC的形状。
,试判断△ABC的形状。
解:由正弦定理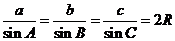 得:
得: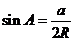 ,
,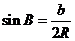 ,
,
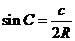 。
。
所以由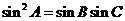 可得:
可得: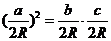 ,即:
,即: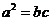 。
。
又已知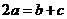 ,所以
,所以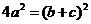 ,所以
,所以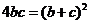 ,即
,即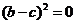 ,
,
因而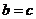 。故由
。故由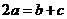 得:
得: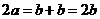 ,
,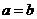 。所以
。所以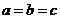 ,△ABC
,△ABC
为等边三角形。
6.在△ABC中,已知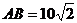 ,A=45°,BC=
,A=45°,BC=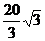 ,求角C。
,求角C。
解:由正弦定理得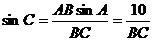 ,又BC=
,又BC=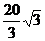 时,故 sinC=
时,故 sinC=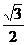 ;
;
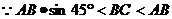
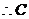 有两解
有两解 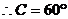 或120°
或120°
综合拔高训练
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com