
题目列表(包括答案和解析)
20、设M为部分正整数组成的集合,数列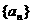 的首项
的首项 ,前n项和为
,前n项和为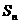 ,已知对任意整数k属于M,当n>k时,
,已知对任意整数k属于M,当n>k时,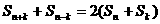 都成立
都成立
(1)设M={1},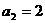 ,求
,求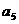 的值;
的值;
(2)设M={3,4},求数列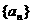 的通项公式。
的通项公式。
19、已知a,b是实数,函数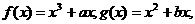
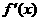 和
和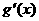 是
是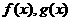 的导函数,若
的导函数,若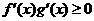 在区间I上恒成立,则称
在区间I上恒成立,则称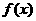 和
和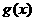 在区间I上单调性一致
在区间I上单调性一致
(1)设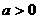 ,若函数
,若函数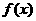 和
和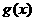 在区间
在区间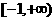 上单调性一致,求实数b的取值范围;
上单调性一致,求实数b的取值范围;
(2)设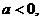 且
且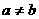 ,若函数
,若函数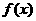 和
和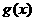 在以a,b为端点的开区间上单调性一致,求|a-b|的最大值
在以a,b为端点的开区间上单调性一致,求|a-b|的最大值
18、如图,在平面直角坐标系 中,M、N分别是椭圆
中,M、N分别是椭圆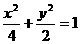 的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k
的顶点,过坐标原点的直线交椭圆于P、A两点,其中P在第一象限,过P作x轴的垂线,垂足为C,连接AC,并延长交椭圆于点B,设直线PA的斜率为k
(1)当直线PA平分线段MN,求k的值;
 (2)当k=2时,求点P到直线AB的距离d;
(2)当k=2时,求点P到直线AB的距离d;
(3)对任意k>0,求证:PA⊥PB
17、请你设计一个包装盒,如图所示,ABCD是边长为60cm的正方形硬纸片,切去阴影部分所示的四个全等的等腰直角三角形,再沿虚线折起,使得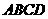 四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm
四个点重合于图中的点P,正好形成一个正四棱柱形状的包装盒,E、F在AB上是被切去的等腰直角三角形斜边的两个端点,设AE=FB=xcm
(1)若广告商要求包装盒侧面积S(cm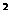 )最大,试问x应取何值?
)最大,试问x应取何值?
(2)若广告商要求包装盒容积V(cm )最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
)最大,试问x应取何值?并求出此时包装盒的高与底面边长的比值。
P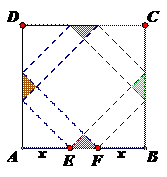

16、如图,在四棱锥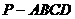 中,平面PAD⊥平面ABCD,
中,平面PAD⊥平面ABCD,
AB=AD,∠BAD=60°,E、F分别是AP、AD的中点
求证:(1)直线EF‖平面PCD;
(2)平面BEF⊥平面PAD
15、在△ABC中,角A、B、C所对应的边为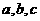
(1)若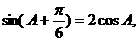 求A的值;
求A的值;
(2)若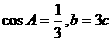 ,求
,求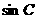 的值.
的值.
(11)设函数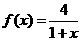 ,若f(a)=2,则实数a=________________________
,若f(a)=2,则实数a=________________________
(12)若直线与直线x-2y+5=0与直线2x+my-6=0互相垂直,则实数m=_____________________
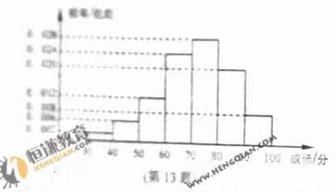
(13)某小学为了解学生数学课程的学习情况,在3000名学生中随机抽取200名,并统计这200名学生的某此数学考试成绩,得到了样本的频率分布直方图(如图)。根据频率分布直方图3000名学生在该次数学考试中成绩小于60分的学生数是_____________________
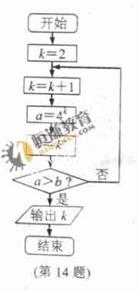
(14)某程序框图如图所示,则该程序运行后输出的k的值是_____________________。
(15)若平面向量α、β 满足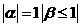 ,且以向量α、β为邻边的平行四边形的面积为
,且以向量α、β为邻边的平行四边形的面积为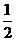 ,则α和β的夹角 θ的取值范围是____________________________。
,则α和β的夹角 θ的取值范围是____________________________。
(16)若实数x,y满足x2+y2+xy=1,则x+y的最大值是___________________________。
(17)若数列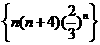 中的最大项是第k项,则k=_______________。
中的最大项是第k项,则k=_______________。
解答题,共72分。解答应写出文字说明、证明过程或演算步骤。
(18)(本题满分14分)已知函数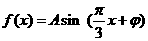 ,
,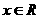 ,
,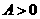 ,
,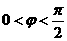 .
.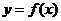 的部分图像,如图所示,
的部分图像,如图所示,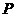 、
、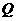 分别为该图像的最高点和最低点,点
分别为该图像的最高点和最低点,点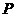 的坐标为
的坐标为 .
.
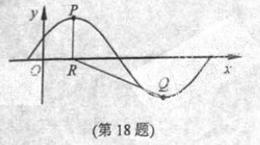
(Ⅰ)求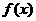 的最小正周期及
的最小正周期及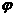 的值;
的值;
(Ⅱ)若点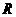 的坐标为
的坐标为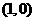 ,
,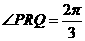 ,求
,求 的值.
的值.
(19)(本题满分14分)已知公差不为0的等差数列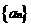 的首项
的首项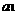
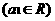 ,且
,且 ,
,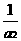 ,
,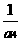 成等比数列.
成等比数列.
(Ⅰ)求数列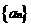 的通项公式;
的通项公式;
(Ⅱ)对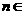 N*,试比较
N*,试比较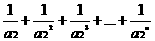 与
与 的大小.
的大小.
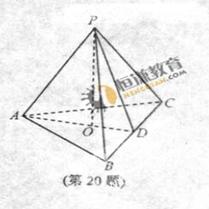
(20)(本题满分14分)如图,在三棱锥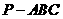 中,
中,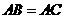 ,
,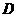 为
为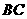 的中点,
的中点,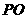 ⊥平面
⊥平面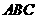 ,垂足
,垂足 落在线段
落在线段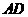 上.
上.
(Ⅰ)证明: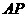 ⊥
⊥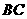 ;
;
(Ⅱ)已知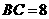 ,
,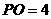 ,
,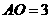 ,
,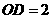 .求二面角
.求二面角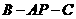 的大小.
的大小.
(21)(本小题满分15分)设函数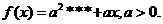
(Ⅰ)求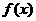 的单调区间
的单调区间
(Ⅱ)求所有实数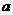 ,使
,使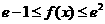 对
对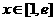 恒成立。
恒成立。
注: 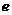 为自然对数的底数。
为自然对数的底数。
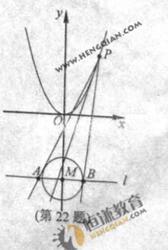
(22)(本小题满分15分)如图,设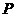 是抛物线
是抛物线 :
:
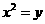 上的动点。过点
上的动点。过点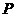 做圆
做圆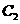 的两条切线,交直线
的两条切线,交直线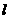 :
: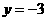 于
于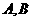 两点。
两点。
(Ⅰ)求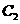 的圆心
的圆心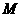 到抛物线
到抛物线  准线的距离。
准线的距离。
(Ⅱ)是否存在点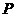 ,使线段
,使线段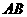 被抛物线
被抛物线 在点
在点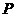 处得切线平分,若存在,求出点
处得切线平分,若存在,求出点 的坐标;若不存在,请说明理由。
的坐标;若不存在,请说明理由。
(1)
若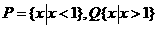 ,则
,则
(A)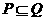 (B)
(B)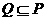 (C)
(C)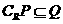 (D)
(D)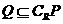
(2)若复数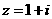 ,
,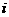 为虚数单位,则
为虚数单位,则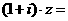
(A)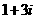 (B)
(B) (C)
(C)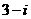 (D)3
(D)3
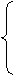 x+2y-5≥0
x+2y-5≥0
(3)若实数x,y满足不等式组 2x+y-7≥0,则3x:4y的最小值是
x≥0,y≥0
(A)13 (B)15 (C)20 (D)28
(4)若直线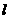 不平行于平面
不平行于平面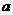 ,且
,且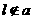 ,则
,则
(A)
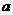 内存在直线与异面
(B)
内存在直线与异面
(B) 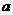 内不存在与
内不存在与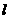 平行的直线
平行的直线
(C)
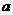 内存在唯一的直线与
内存在唯一的直线与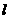 平行
(D)
平行
(D) 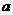 内的直线与
内的直线与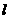 都相交
都相交
(5)在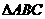 中,角A,B,C,所对的边分别为a,b,c.若
中,角A,B,C,所对的边分别为a,b,c.若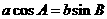 ,则
,则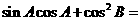
(A)- 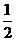 (B)
(B)
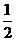 (C) -1
(D) 1
(C) -1
(D) 1
(6)若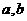 为实数,则“
为实数,则“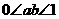 ”是“
”是“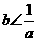 ”的
”的
(A)充分而不必要条件 (B)必要而不充分条件
(C)充分必要条件 (D)既不充分也不必要条件
(7)几何体的三视图如图所示,则这个几何体的直观图可以是
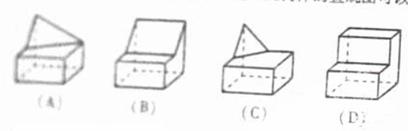
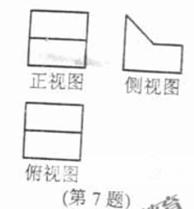
(8)从已有3个红球、2个白球的袋中任取3个球,则所取的3个球中至少有1个白球的概率是
(A)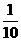 (B)
(B)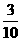 (C)
(C)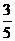 (D)
(D)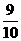
(9)已知椭圆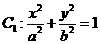 (a>b>0)与双曲线
(a>b>0)与双曲线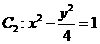 有公共的焦点,C2的一条渐近线与C1C2的长度为直径的圆相交于A,B两点。若C1恰好将线段AB三等分,则
有公共的焦点,C2的一条渐近线与C1C2的长度为直径的圆相交于A,B两点。若C1恰好将线段AB三等分,则
(A)a2 =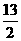 (B)a2=13
(C)b2=
(B)a2=13
(C)b2=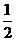 (D)b2=2
(D)b2=2
(10)设函数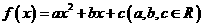 ,若
,若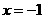 为函数
为函数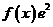 的一个极值点,则下列图象不可能为
的一个极值点,则下列图象不可能为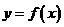 的图象是
的图象是
非选择题部分 (共100分)
请用0.5毫米黑色墨水签字笔或钢笔将答案写在答题纸上,不能答在试题卷上
若需在答题纸上作图,可先使用铅笔作图,确定后必须使用黑色字迹的签字笔或钢笔描黑
21.(本小题满分14分)
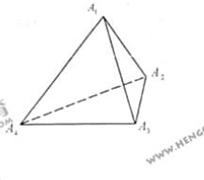 (1)如图,对于任意给定的四面体
(1)如图,对于任意给定的四面体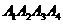 ,找出依次排列的四个相互平行的
,找出依次排列的四个相互平行的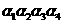 ,使得
,使得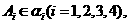 且其中每相邻两个平面间的距离都相等;
且其中每相邻两个平面间的距离都相等;
(2)给定依次排列的四个相互平行的平面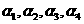 ,其中每相邻两个平面间的距离为
,其中每相邻两个平面间的距离为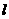 ,若一个正四面体
,若一个正四面体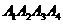 的四个顶点满足:
的四个顶点满足: 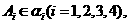 求该正四面体
求该正四面体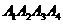 的体积
的体积
20.(本小题满分13分)
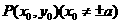 是双曲线E:
是双曲线E: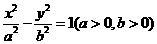 上一点,M,N分别是双曲线E的左右顶点,直线PM,PN的斜率之积为
上一点,M,N分别是双曲线E的左右顶点,直线PM,PN的斜率之积为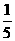 。
。
(1)求双曲线的离心率;
(2)过双曲线E的右焦点且斜率未1的直线交双曲线于A,B两点,O为坐标原点,C为双曲线上一点,满足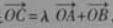 ,求
,求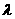 的值。
的值。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com