
题目列表(包括答案和解析)
7. (中山市高三级2008-2009学年度第一学期期末统一考试)
已知向量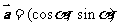 ,
, 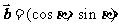 ,
, 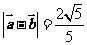 .
.
(Ⅰ) 求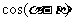 的值;
的值;
(Ⅱ) 若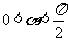 ,
, 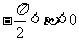 , 且
, 且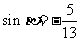 , 求
, 求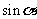
解:(Ⅰ)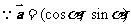 ,
, 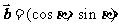 ,
,
 .
.
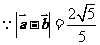 ,
, 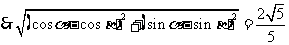 ,
,
即
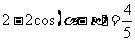 ,
, 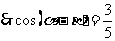 .
.
(Ⅱ)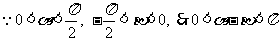 ,
,
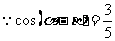 ,
, 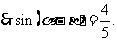
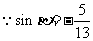 ,
, 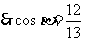 ,
,
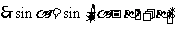
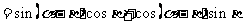
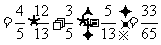 .
.
6. (广东省四校联合体08年第一次联考)设函数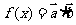 ,其中向量
,其中向量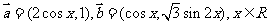 ,若函数
,若函数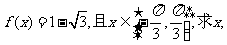
解:(1)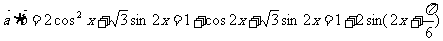

综合拔高训练
5. 设向量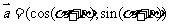 ,
,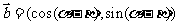 ,且
,且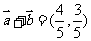 .
.
(1)求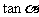 ;
;
(2)求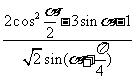 .
.
解:(1)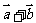
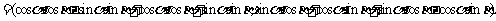
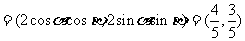
∴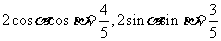
∴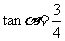
(2)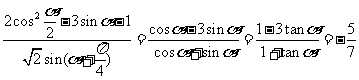 .
.
5.求值: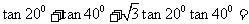 _____________
_____________
解析: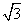 .
.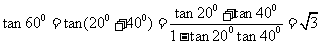
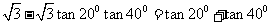
4.设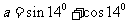 ,
,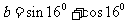 ,
,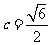 ,
,
则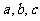 大小关系( )
大小关系( )
A
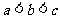 B
B

C
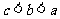 D
D
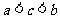
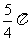 C.
C. 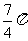 D.
D. 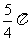 或
或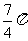
解析:D 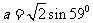 ,
,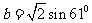 ,
,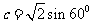
3.(广东深圳外国语学校2008-2009学年高三第二次月考)已知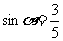 ,则
,则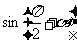 的值为( )
的值为( )
A.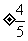 B.
B.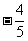 C.
C.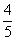 D.
D. 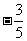
解析: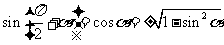 =
= 选A
选A
2.( 汕头金山中学2008-2009学年度上学期高三期末考试)
已知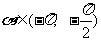 ,且
,且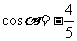 ,则
,则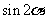 等于( )
等于( )
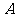 .
.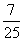
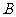 .
.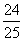
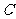 .
.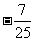
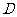 .
.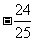
解析:由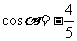 且
且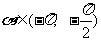 知
知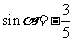 故
故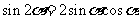 =
=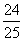 选B
选B
6.求证: 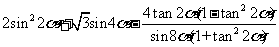 .=
.=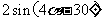
证明:左边=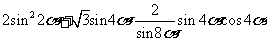 =
=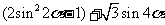
= =
=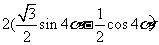 =
=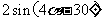 =右边
=右边
[方法技巧] 利用万能公式得出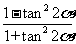 =
=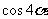 ,
,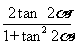 =
=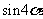 可简化过程.
可简化过程.
★抢 分 频 道
基础巩固训练
1已知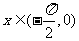 ,
,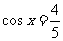 ,则
,则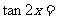 ( )
( )
A
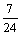 B
B
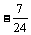 C
C
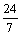 D
D
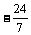
解析:D 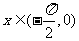 ,
,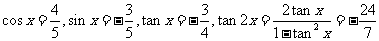
5.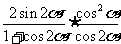 =( )
=( )
A、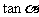 B、
B、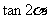 C、1
D、
C、1
D、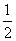
B[解析]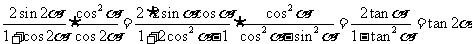
4.在△ABC中,角A,B,C所对边分别为a,b,c,且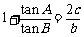 ,求角A;
,求角A;
解析: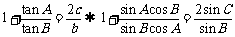 ,即
,即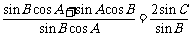 ,
,
∴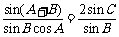 ,∴
,∴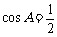 .∵
.∵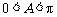 ,∴
,∴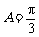 .
.
考点2: 三角式的化简与证明
题型1:利用正、余弦定理和三角函数的恒等变换进行化简求值.
例1.
化简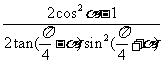
[解题思路]对三角函数式化简结果的一般要求:①函数种类最少;②项数最少;③函数次数最低;④能求值的求出值;⑤尽量使分母不含三角函数;⑥尽量使分母不含根式.
[解析]原式=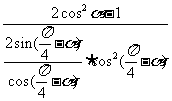 =
=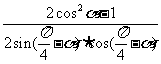
=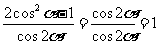
[名师指引]在三角式的化简方向一般为降次,消项.
例2:证明tan-tan=
[解题思路]细心观察已知等式中的角,发现它们有隐含关系:+=2x,-=x
 -=x ∴sinx=sincos-cossin ①
-=x ∴sinx=sincos-cossin ①
又cosx+cos2x=2coscos ②
①÷②即得:
=-=tan-tan.
[名师指引]三角恒等式的证明在高考中出现较少,方法与化简类似.
[新题导练]
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com