1．已知抛物线的顶点在原点，焦点在y轴上，抛物线上的点P(m，－2)到焦点的距离为4，则m的值为(　)

A．4　　　　　　　　　　　 B．－2

C．4或－4 　　　　　　　　　　　 D．12或－2

解析：设标准方程为x²＝－2py(p>0)，

由定义知P到准线距离为4，

故+2＝4，∴p＝4，

∴方程为x²＝－8y，代入P点坐标得m＝±4.

答案：C

12．已知某校高三文科班学生的化学与物理的水平测试成绩抽样统计如下表，若抽取学生n人，成绩分为A(优秀)、B(良好)、C(及格)三个等级，设x，y分别表示化学成绩与物理成绩．例如：表中化学成绩为B等级的共有20+18+4＝42人，已知x与y均为B等级的概率是0.18.

(1)求抽取的学生人数；

(2)设在该样本中，化学成绩优秀率是30%，求a，b的值；

(3)在物理成绩为C等级的学生中，已知a≥10，b≥8，求化学成绩为A等级的人数比C等级的人数少的概率.

y 人数 x	A	B	C
A	7	20	5
B	9	18	6
C	a	4	b

解：(1)由题意可知＝0.18，得n＝100.

故抽取的学生人数是100.

(2)由(1)知n＝100，所以＝0.3，故a＝14，

而7+9+a+20+18+4+5+6+b＝100，故b＝17.

(3)由(1)易知a+b＝31，且a≥10，b≥8，

满足条件的(a，b)有(10,21)，(11,20)，(12,19)，…，

(23,8)，共有14组，其中b>a的有6组，

则所求概率为P＝＝.

11．一汽车厂生产A，B，C三类轿车，每类轿车均有舒适型和标准型两种型号，某月的产量如下表(单位：辆)：

按类型用分层抽样的方法在这个月生产的轿车中抽取50辆，其中有A类轿车10辆．

(1)求z的值；

(2)用分层抽样的方法在C类轿车中抽取一个容量为5的样本．将该样本看成一个总体，从中任取2辆，求至少有1辆舒适型轿车的概率；

(3)用随机抽样的方法从B类舒适型轿车中抽取8辆，经检测它们的得分如下：9.4,8.6,9.2,9.6,8.7,9.3,9.0，8.2.把这8辆轿车的得分看作一个总体，从中任取一个数，求该数与样本平均数之差的绝对值不超过0.5的概率．

解：(1)设该厂本月生产轿车为n辆，由题意得

＝，所以n＝2 000，

则z＝2 000－(100+300)－(150+450)－600＝400.

(2)设所抽样本中有a辆舒适型轿车，由题意＝，得a＝2.

因此抽取的容量为5的样本中，有2辆舒适型轿车，3辆标准型轿车．

用A₁，A₂表示2辆舒适型轿车，用B₁，B₂，B₃表示3辆标准型轿车，用E表示事件“在该样本中任取2辆，其中至少有1辆舒适型轿车”，则基本事件空间包含的基本事件有：(A₁，A₂)，(A₁，B₁)，(A₁，B₂)，(A₁，B₃)，(A₂，B₁)，(A₂，B₂)，(A₂，B₃)，(B₁，B₂)，(B₁，B₃)，(B₂，B₃)，共10个．

事件E包含的基本事件有：(A₁，A₂)，(A₁，B₁)，(A₁，B₂)，(A₁，B₃)，(A₂，B₁)，(A₂，B₂)，(A₂，B₃)，共7个，

故P(E)＝，即所求概率为.

(3)样本平均数＝(9.4+8.6+9.2+9.6+8.7+9.3+9.0+8.2)＝9.

设D表示事件“从样本中任取一数，该数与样本平均数之差的绝对值不超过0.5”，则基本事件空间中有8个基本事件，事件D包括的基本事件有：9.4,8.6，9.2，8.7,9.3,9.0，共6个，所以P(D)＝＝，

即所求概率为.

10．某单位有工程师6人，技术员12人，技工18人，要从这些人中抽取一个容量为n的样本．如果采用系统抽样法和分层抽样方法抽取，不用剔除个体；如果样本容量增加一个，则在采用系统抽样时，需要在总体中先剔除1个个体．求样本容量n.

解：总体容量为6+12+18＝36(人)．当样本容量是n时，由题意知，系统抽样的间隔为，分层抽样的比例是，抽取工程师×6＝(人)，抽取技术员×12＝(人)，抽取技工×18＝(人)．所以n应是6的倍数，36的约数，即n＝6,12,18,36.

当样本容量为(n+1)时，系统抽样的间隔为，因为必须是整数，所以n只能取6，即样本容量n＝6.

9．最近网络上流行一种“QQ农场游戏”，这种游戏通过虚拟软件模拟种植与收获的过程．为了了解本班学生对此游戏的态度，高三(6)班计划在全班60人中展开调查，根据调查结果，班主任计划采用系统抽样的方法抽取若干名学生进行座谈，为此先对60名学生进行编号为：01,02,03，…，60，已知抽取的学生中最小的两个编号为03,09，则抽取的学生中最大的编号为________．

解析：由最小的两个编号为03,09可知，抽取人数的比例为，即抽取10名同学，其编号构成首项为3，公差为6的等差数列，故最大编号为3+9×6＝57.

答案：57

8．(2010·广东高考)某单位200名职工的年龄分布情况如图，现要从中抽取40名职工作样本．用系统抽样法，将全体职工随机按1-200编号，并按编号顺序平均分为40组(1-5号，6-10号，…，196-200号)．若第5组抽出的号码为22，则第8组抽出的号码应是________．若用分层抽样方法，则40岁以下年龄段应抽取________人．

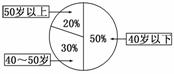
解析：法一：由系统抽样知第1组抽出的号码为2，则第8组抽出的号码为2+5×7＝37；当用分层抽样抽取，则40岁以下年龄段应抽取×40＝20名．

法二：由系统抽样知，第5组抽出的号码为22，而分段间隔为5，则第6组抽取的应为27，第7组抽取的应为32，第8组抽取的号码应为37.

由图知40岁以下的人数为100人，则抽取的比例为＝，

∴100×＝20为抽取人数．

答案：37　20

7．某大学共有学生5 600人，其中专科生1300人、本科生3 000人、研究生1 300人，现采用分层抽样的方法调查学生利用因特网查找学习资料的情况，抽取的样本为280人，则在专科生、本科生与研究生这三类学生中分别抽取的人数为________．

解析：由已知可得＝＝＝，

∴x＝z＝65，y＝150.

答案：65,150,65

6．(2010·东城模拟)在100个零件中，有一级品20个，二级品30个，三级品50个，从中抽取20个作为样本．

①采用随机抽样法：抽签取出20个样本；

②采用系统抽样法：将零件编号为00,01，……，99，然后平均分组抽取20个样本

③采用分层抽样法：从一级品，二级品，三级品中抽取20个样本．

下列说法中正确的是(　)

A．无论采用哪种方法，这100个零件中每一个零件被抽到的概率都相等

B．①②两种抽样方法，这100个零件中每一个零件被抽到的概率都相等；③并非如此

C．①③两种抽样方法，这100个零件中每一个零件被抽到的概率都相等；②并非如此

D．采用不同的抽样方法，这100个零件中每一个零件被抽到的概率是各不相同的

解析：上述三种方法均是可行的，每个个体被抽到的概率均等于＝.

答案：A

5．(2010·山东烟台)某高中共有学生2 000名，各年级的男生、女生人数如下表．已知在全校学生中随机抽取1名，抽到二年级女生的概率是0.19，现用分层抽样的方法在全校抽取64名学生，则应在三年级抽取的学生人数为(　)

A.24 　　　　　　　 　　 B．18

C．16　 　　　　　　　　　　　 D．12

解析：根据题意可知二年级女生的人数应为2 000×0.19＝380人，故一年级共有750人，二年级共有750人，这两个年级均应抽取64×＝24人，则应在三年级抽取的学生人数为64－24×2＝16人．

答案：C

4．某工厂在12月份共生产了3600双皮靴，在出厂前要检查这批产品的质量，决定采用分层抽样的方法进行抽取，若从一、二、三车间抽取的产品数分别为a、b、c，且a、b、c构成等差数列，则第二车间生产的产品数为(　)

A．800　 　　　　　　　 B．1 000

C．1 200　 　　　　　　 D．1 500

解析：因为a、b、c成等差数列，所以2b＝a+c，即第二车间抽取的产品数占抽样产品总数的三分之一，根据分层抽样的性质可知，第二车间生产的产品数占总数的三分之一，即为1 200双皮靴．

答案：C