
题目列表(包括答案和解析)
5.(2007·广东)若函数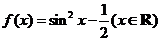 ,则
,则 是(D )
是(D )
A.最小正周期为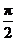 的奇函数 B.最小正周期为
的奇函数 B.最小正周期为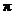 的奇函数
的奇函数
C.最小正周期为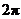 的偶函数 D.最小正周期为
的偶函数 D.最小正周期为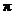 的偶函数
的偶函数
[剖析]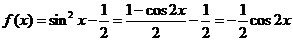 ,
,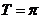 ,且为偶函数.
,且为偶函数.
[答案]D.
4. 已知向量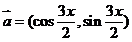 ,
,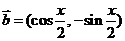 ,且
,且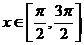
(1)求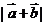 的取值范围;
的取值范围;
(2)若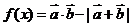 ,试求
,试求 的取小值,并求此时
的取小值,并求此时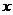 的值。
的值。
解: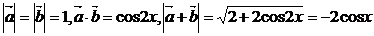
(1)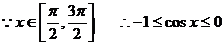
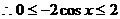
即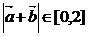 ………………………………6分
………………………………6分
(2)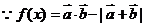
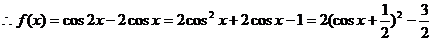
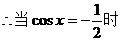
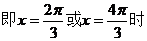
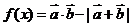 的最小值为 -
的最小值为 -
考点3 周期性与奇偶性问题
题型 .研究三角函数的奇偶性和求周期
[例1](潮南区08-09学年度第一学期期末高三级质检第(1)(3)问)
已知函数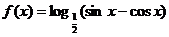 (1)求f(x)的定义域;(2)判断f(x)的奇偶性。
(1)求f(x)的定义域;(2)判断f(x)的奇偶性。
[解题思路]用奇偶性的定义和性质进行判断
解析:(1)要使f(x)有意义,必须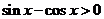 ,即
,即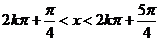
得f(x)的定义域为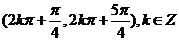
(2)因f(x)的定义域为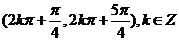 ,关于原点不对称,所以f(x)为非奇非偶函数.
,关于原点不对称,所以f(x)为非奇非偶函数.
[名师指引]讨论函数的奇偶性,其前提条件是函数的定义域必须关于原点对称.
若函数f(x)为奇函数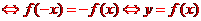 的图像关于原点对称.
的图像关于原点对称.
若函数f(x)为偶函数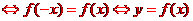 的图像关于y轴对称.
的图像关于y轴对称.
[例2](08江苏卷)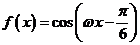 的最小正周期为
的最小正周期为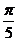 ,其中
,其中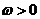 ,则
,则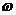 = .
= .
[解题思路]代公式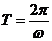
解析: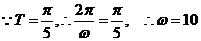
[名师指引]先将解析式化为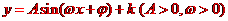 的形式,再用公式
的形式,再用公式
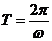 进行处理.
进行处理.
[新题导练]
3.设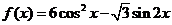 .求
.求 的最大值及最小正周期.
的最大值及最小正周期.
解: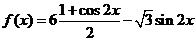
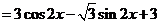
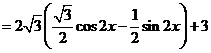
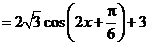 .
.
故 的最大值为
的最大值为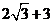 ;最小正周期
;最小正周期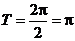 .
.
2.( 广东省北江中学2009届高三上学期12月月考)已知函数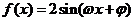 对任意
对任意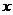 都有
都有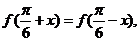 则
则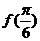 等于( )
等于( )
 A.
A. 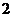 或
或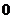 B.
B. 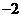 或
或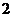 C.
C. 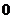 D.
D. 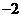 或
或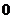
解析: 由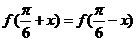 ,函数图象关于
,函数图象关于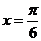 ,
,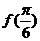 是最大值或最小值选B
是最大值或最小值选B
考点2 值域与最值问题
题型1.化为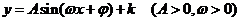 的形式
的形式
[例1]. (2009年广东省广州市高三年级调研测试)
已知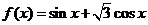
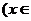 R
R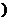 .
.
(1)求函数 的最小正周期;
的最小正周期;
(2)求函数 的最大值,并指出此时
的最大值,并指出此时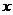 的值.
的值.
[解题思路]利用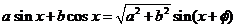 对解析式进行化简,再进一步处理.
对解析式进行化简,再进一步处理.
解:(1)∵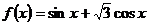
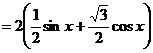
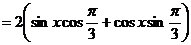
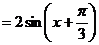
∴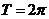 .
.
(2) 当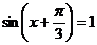 时,
时,  取得最大值, 其值为2
.
取得最大值, 其值为2
.
此时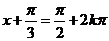 ,即
,即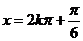
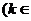 Z
Z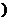 .
.
[名师指引]研究三角函数的图象与性质一般先将解析式化为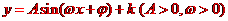 的形式,再研究函数的性质. 利用整体代换的思想求出函数的最大值和最小值是解题的关键.
的形式,再研究函数的性质. 利用整体代换的思想求出函数的最大值和最小值是解题的关键.
题型2.通过换元用二次函数的知识研究值域或最值.
[例2]
|
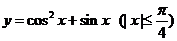 的最大值和最小值.
的最大值和最小值.
[解题思路]将余弦化为正弦,再换元处理.
[解析]设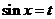 ,则
,则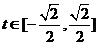
所以
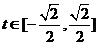
故当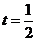 即
即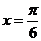 时,
时,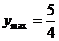 ,当
,当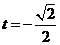 即
即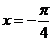 时,
时,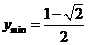 .
.
[名师指引]若函数出现既有一次项又有二项,一般都要利用二次函数的思想.
[新题导练]
1.画出函数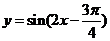 在区间
在区间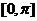 上的图像.
上的图像.
[解析](1)列表如下:
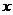 |
0 |
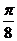 |
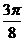 |
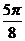 |
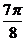 |
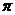 |
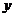 |
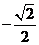 |
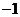 |
0 |
1 |
0 |
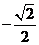 |
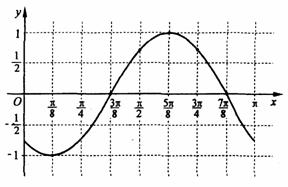 (2)描点、连线(如图3-3-3)
(2)描点、连线(如图3-3-3)
3.重难点:合理利用三角变换公式化简三角函数解析式,利用三角函数图象与性质处理与不等关系相关的问题
(1)利用单调性处理不等关系
问题1. (08四川)设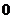 ≤
≤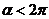 ,若
,若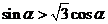 ,则
,则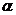 的取值范围是
的取值范围是
(A)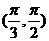 (B)
(B)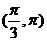 (C)
(C)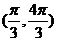 (D)
(D)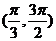
点拨:处理三角函数的问题,除于记住定义域、值域和最值、单调性、奇偶性、周期性之外,还要记对称轴、对称中心、正负区间.
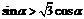 ,即
,即 ,即
,即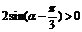 ,即
,即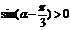 ;
;
又由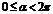 ,得
,得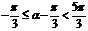 ;综上,
;综上,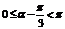 ,即
,即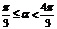 .选C.
.选C.
(2)研究三角函数的性质
问题2. (08安徽卷)已知函数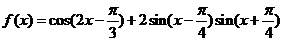
(Ⅰ)求函数 的最小正周期和图象的对称轴方程
的最小正周期和图象的对称轴方程
(Ⅱ)求函数 在区间
在区间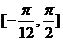 上的值域
上的值域
点拨:处理三角函数的图象与性质的问题关键是将解析式化为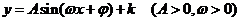 的形式;求三角函数的值域先考虑角的范围,再借助于图象.
的形式;求三角函数的值域先考虑角的范围,再借助于图象.
解:(1)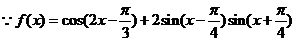
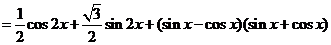
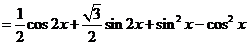
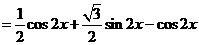
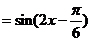
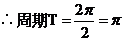 ,由
,由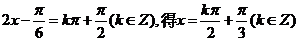
 函数图象的对称轴方程为
函数图象的对称轴方程为 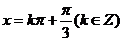
(2)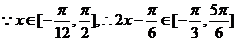
因为 在区间
在区间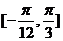 上单调递增,在区间
上单调递增,在区间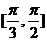 上单调递减,
上单调递减,
所以 当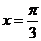 时,
时, 取最大值 1
取最大值 1
又 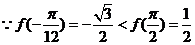 ,当
,当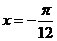 时,
时, 取最小值
取最小值
所以 函数  在区间
在区间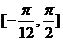 上的值域为
上的值域为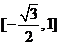
★热 点 考 点 题 型 探 析
考点1 作三角函数的图象
题型1:作正弦函数的图象
[例1](2007·天津改编)画出函数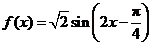 在一个周期内的图像.
在一个周期内的图像.
[解题思路]三角函数作图的三个主要步骤(列表、描点、连线).五个特殊点的选取.
[解析](1)列表如下:
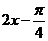 |
0 |
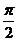 |
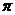 |
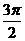 |
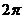 |
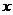 |
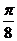 |
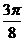 |
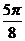 |
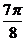 |
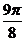 |
 |
0 |
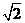 |
0 |
-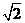 |
0 |
(2)描点、连线(如图3-3-2)
|
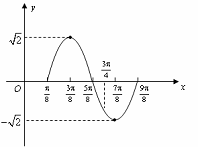
[名师指引]五点法作图的技巧:
函数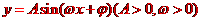 的图像在一个周期内的五点横向间距必相等,为
的图像在一个周期内的五点横向间距必相等,为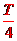 ,于是五点横坐标依次为
,于是五点横坐标依次为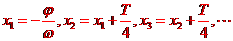 ,这样,不仅可以快速求出五点坐标,也可在求得
,这样,不仅可以快速求出五点坐标,也可在求得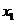 的位置后,用圆规截取其他四点,从而准确作出图像.
的位置后,用圆规截取其他四点,从而准确作出图像.
题型2.借助于三角函数的图象处理有关问题
问题2. (2007·天津)设函数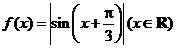 ,则
,则 ( )
( )
A、在区间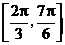 上是增函数 B、在区间
上是增函数 B、在区间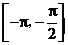 上是减函数
上是减函数
C、在区间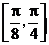 上是增函数 D、在区间
上是增函数 D、在区间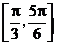 上是减函数
上是减函数
[解题思路]作出图象,一目了然
[解析]函数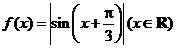 的图象如下图
的图象如下图
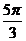
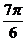
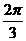
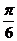
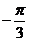
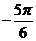
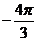
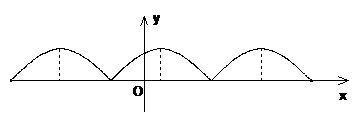
选 A.
[名师指引]数形结合在处理三角函数的单调性的有关问题时起到关键作用.
[新题导练]
2.难点:化简三角函数式的过程.
1.重点:熟练掌握利用三角恒等变换化简三角函数解析式式,熟悉正弦函数和余弦函数的图象与性质。
9.扇形的中心角为120°,则此扇形的面积与其内切圆的面积之比为________.
解析:设内切圆的半径为r,
扇形半径为R,则(R-r)sin60°=r.
∴R=(1+)r,
∴==()2=(1+)2=.
8.在直角坐标系中,O是原点,A(,1),将点A绕O逆时针旋转90°到B点,则B点坐标为__________.
解析:依题意知OA=OB=2,∠AOx=30°,∠BOx=120°,
所以x=2cos120°=-1,y=2sin120°=,即B(-1,).
答案:(-1,)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com