
题目列表(包括答案和解析)
1.(2008年佛山)证明:若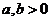 ,则
,则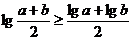
[解析]当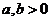 时,
时,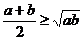 ,
,
两边取对数,得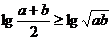 ,
,
又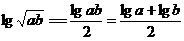
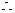 当
当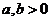 时
时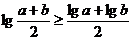
2.比较复杂的命题,有时需要多种证明方法综合运用,各取所长。
★热点考点题型探析★
考点1 综合法
题型:用综合法证明数学命题
[例1 ] (东莞2007-2008学年度第一学期高三调研测试)
对于定义域为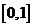 的函数
的函数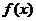 ,如果同时满足以下三条:①对任意的
,如果同时满足以下三条:①对任意的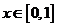 ,总有
,总有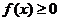 ;②
;②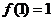 ;③若
;③若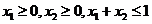 ,都有
,都有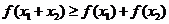 成立,则称函数
成立,则称函数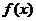 为理想函数.
为理想函数.
(1) 若函数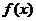 为理想函数,求
为理想函数,求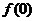 的值;
的值;
(2)判断函数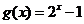 (
(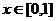 )是否为理想函数,并予以证明;
)是否为理想函数,并予以证明;
[解题思路]证明函数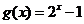 (
(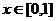 )满足三个条件
)满足三个条件
[解析](1)取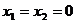 可得
可得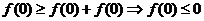 .
.
又由条件①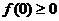 ,故
,故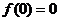 .
.
(2)显然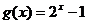 在[0,1]满足条件①
在[0,1]满足条件①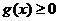 ;
;
也满足条件②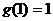 .若
.若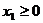 ,
,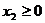 ,
,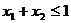 ,则
,则
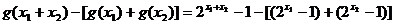
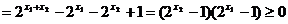 ,即满足条件③,
,即满足条件③,
故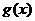 理想函数.
理想函数.
[名师指引]紧扣定义,逐个验证
[新题导练]
1.从命题的特点、形式去选择证明方法
①一般地,结论中出现“至多”“至少”“唯一”等词语,或否定性命题,或要讨论的情况很复杂的,可以考虑用反证法②一般地,含分式、根式的不等式,或从条件出发思路不明显的命题,可以考虑用分析法③命题的结论有明确的证明方向的,适宜用综合法
问题1:对于任意非零实数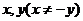 ,等式
,等式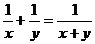 总不成立
总不成立
点拨:从命题的形式特点看,适合用反证法证明
3.假设原命题的结论不成立,经过正确的推理,最后得出矛盾,由此说明假设错误,从而证明了原命题成立,这样的方法叫反证法;它是一种间接的证明方法.用这种方法证明一个命题的一般步骤:(1) 假设命题的结论不成立; (2) 根据假设进行推理,直到推理中导出矛盾为止
(3) 断言假设不成立(4) 肯定原命题的结论成立
★重难点突破★
重点:能熟练运用三种证明方法分析问题或证明数学命题
难点:运用三种方法提高分析问题和解决问题的能力
重难点:在函数、三角变换、不等式、立体几何、解析几何等不同的数学问题中,选择好证明方法并运用三种证明方法分析问题或证明数学命题
2. 分析法是从要证明的结论出发,逐步寻求推证过程中,使每一步结论成立的充分条件,直到最后,把要证明的结论归结为判定一个明显成立的条件(已知条件、定义、公理、定理等)为止的证明方法。
1. 综合法是由原因推导到结果的证明方法,它是利用已知条件和某些数学定义、公理、定理等,经过一系列的推理论证,最后推导出所要证明的结论成立的证明方法。
21. (12分)若函数y=f(x)是周期为2的偶函数,当x∈[2,3]时,f(x)=x-1.在y=f(x)的图象上有两点A、B,它们的纵坐标相等,横坐标都在区间[1,3]上,定点C的坐标为(0,a)(其中2<a<3),
(1) 求当x∈[1,2]时,f(x)的解析式;
(2) 定点C的坐标为(0,a)(其中2<a<3),求△ABC面积的最大值.
[解:析](1)∵f(x)是以2为周期的周期函数,当x∈[2,3]时,f(x)=x-1,
∴当x∈[0,1]时,f(x)=f(x+2)=(x+2)-1=x+1. …………1分
∵f(x)是偶函数,∴当x∈[-1,0]时,f(x)=f(-x)=-x+1, …………2分
当x∈[1,2]时,f(x)=f(x-2)=-(x-2)+1=-x+3. …………4分
(2)设A、B的横坐标分别为3-t,t+1,1≤t≤2,则|AB|=(t+1)-(3-t)=2t-2, …………6分
∴△ABC的面积为S=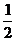 (2t-2)·(a-t)=-t2+(a+1)t-a(1≤t≤2)=-(t-
(2t-2)·(a-t)=-t2+(a+1)t-a(1≤t≤2)=-(t-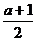 )2+
)2+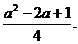
∵2<a<3,∴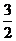 <
<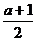 <2.当t=
<2.当t=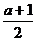 时,S最大值=
时,S最大值=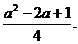 …………12分
…………12分
20.(14分)设函数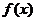 是定义在
是定义在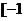 ,0)∪(0,
,0)∪(0,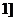 上的奇函数,当xÎ
上的奇函数,当xÎ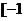 ,0)时,
,0)时,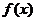 =
=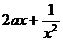 .
.
(1) 求当xÎ(0,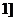 时,
时,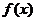 的表达式;
的表达式;
(2) 若a>-1,判断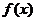 在(0,
在(0, 上的单调性,并证明你的结论.
上的单调性,并证明你的结论.
[解析](1)设xÎ(0, ,则
,则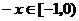 ,…………2分
,…………2分
所以f(-x)=
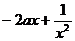 ,…………4分
,…………4分
又因为f(-x)=-f(x),所以f(x)=
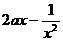 xÎ(0,
xÎ(0,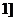 .
…………6分
.
…………6分
(2) xÎ(0,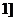 时,f(x)=
时,f(x)= 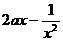 ,
,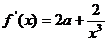 ,
…………10分
,
…………10分
x3Î(0,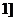 ,
,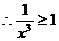 ,
…………12分
,
…………12分
又a>-1,所以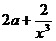 >0,即
>0,即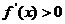 ,所以f(x)在(0,
,所以f(x)在(0,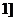 上递增. …………14分
上递增. …………14分
19. (高州中学09届模拟14分)已知函数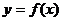 ,若存在
,若存在 ,则
,则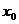
称是函数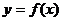 的一个不动点,设
的一个不动点,设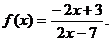
(Ⅰ)求函数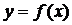 的不动点;
的不动点;
(Ⅱ)对(Ⅰ)中的二个不动点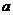 、
、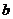 (假设
(假设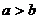 ),求使
),求使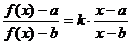
恒成立的常数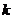 的值;
的值;
解:(Ⅰ)设函数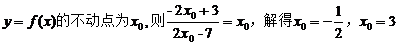 …7分
…7分
(Ⅱ)由(Ⅰ)可知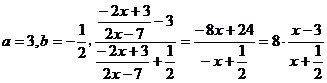
可知使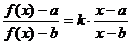 恒成立的常数
恒成立的常数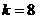 . ……………………14分
. ……………………14分
18.(14分) 已知函数y=f(x)=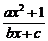 (a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<
(a,b,c∈R,a>0,b>0)是奇函数,当x>0时,f(x)有最小值2,其中b∈N且f(1)<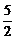 .试求函数f(x)的解析式
.试求函数f(x)的解析式
[解析]∵f(x)是奇函数,∴f(-x)=-f(x),
即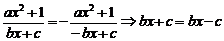 ∴c=0, ……………4分
∴c=0, ……………4分
∵a>0,b>0,x>0,∴f(x)=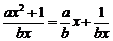 ≥2
≥2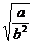 , …………6分
, …………6分
当且仅当x=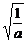 时等号成立,于是2
时等号成立,于是2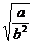 =2,∴a=b2, …………8分
=2,∴a=b2, …………8分
由f(1)<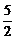 得
得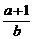 <
<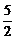 即
即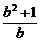 <
<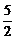 , ………10分
, ………10分
∴2b2-5b+2<0,解得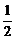 <b<2, …………12分
<b<2, …………12分
又b∈N,∴b=1,∴a=1,∴f(x)=x+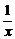 . …………14分
. …………14分
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com