6．设p：函数f(x)＝2^|x－a|在区间(4，+∞)上单调递增，如果“綈p”是真命题．那么实数a的取值范围是(　)

A．[4，+∞)　 　　　　　　　　 B．(4，+∞)

C．[2，+∞)　 　　　　　　　　 D．(2，+∞)

解析：f(x)＝故f(x)在[a，+∞)上是增函数．若p真，则a≤4，∴“綈p”为真时，a>4.

答案：B

5．(2011·咸阳模拟)已知p：x²－x<0，那么命题p的一个必要不充分条件是(　)

A．0<x<1　 　　　　　　　　　　　 B．－1<x<1

C. <x<　 　　　　　　　　　　　　 D. <x<2

解析：由x²－x<0得0<x<1.

设p的一个必要不充分条件为q，则p⇒q，但q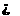p.

答案：B

4．有下列命题：

①“若xy＝0，则|x|+|y|＝0”的逆命题；

②“若a＞b，则a+c＞b+c”的否命题；

③“矩形的对角线互相垂直”的逆否命题．

其中真命题共有(　)

A．1个　 　　　　　　　　　　　　　 B．2个

C．3个　 　　　　　　　　　　　　　 D．4个

解析：①是真命题，②是真命题，③是假命题．

答案：B

3．下列说法中正确的是(　)

A．一个命题的逆命题为真，则它的逆否命题一定为真

B．“a>b”与“a+c>b+c”不等价

C．“a²+b²＝0，则a，b全为0”的逆否命题是“若a，b全不为0，则a²+b²≠0”

D．一个命题的否命题为真，则它的逆命题一定为真

解析：否命题和逆命题是互为逆否命题，有着一致的真假性．

答案：D

2．“k＝1”是“直线x－y+k＝0与圆x²+y²＝1相交”的(　)

A．充分而不必要条件　 　　　　　　　　 B．必要而不充分条件

C．充分必要条件　 　　　　　　　　　　　　 D．既不充分也不必要条件

解析：当k＝1时，圆心到直线的距离d＝＝<1.此时直线与圆相交，所以充分性成立．反之，当直线与圆相交时，d＝<1，|k|<，不一定k＝1，所以必要性不成立．

答案：A

1．(2011·聊城模拟)已知p：>2，q：<1，则q是p的(　)

A．充分不必要条件　　 B．必要不充分条件

C．充要条件　 　　　　　　　　 　　D．既不充分又不必要条件

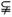解析：p：0<x<，q：0≤x<1，　 [0,1)．

答案：B

7．定义在R上的函数f(x)既是偶函数又是周期函数，若f(x)的最小正周期是π，且当x∈[0，]时，f(x)＝sinx，则f()的值为________．

解析：f()＝f(－)＝f()＝sin＝.

6．若函数y＝2cosωx在区间[0，]上递减，且有最小值1，则ω的值可以是(　)

A．2　 　　　　　　　　　　　　　　　 B.

C．3　 　　　　　　　　　　　　　　　 D.

解析：由y＝2cosωx在[0，π]上是递减的，且有最小值为1，则有f(π)＝1，即2×cos(ω×π)＝1⇒cosω＝.检验各数据，得出B项符合．

答案：B

5．已知函数f(x)＝sinωx+cosωx(ω>0)，y＝f(x)的图象与直线y＝2的两个相邻交点的距离等于π，则f(x)的单调递增区间是(　)

A.kπ－，kπ+，k∈Z

B.kπ+，kπ+，k∈Z

C.kπ－，kπ+，k∈Z

D.kπ+，kπ+，k∈Z

解析：f(x)＝sinωx+cosωx＝2sin(ωx+)(ω>0)．

∵f(x)图象与直线y＝2的两个相邻交点的距离等于π，恰好是f(x)的一个周期，∴＝π，ω＝2.f(x)＝2sin(2x+)．

故其单调增区间应满足2kπ－≤2x+≤2kπ+(k∈Z)．kπ－≤x≤kπ+(k∈Z)．

答案：C

4．已知函数y＝sinx的定义域为[a，b]，值域为[－1，]，则b－a的值不可能是(　)

A.　 　　　　　　　　　 B.

C．π　 　　　　　　　　 D.

解析：画出函数y＝sinx的草图(图略)，分析知b－a的取值范围为[，]．

答案：A