
题目列表(包括答案和解析)
2.难点:能利用超几何分布, 二项分布及n次独立重复实验解决一些简单的实际问题
1.重点:理解超几何分布及其导出过程.了解条件概率和两个事件相互独立的概念,能理解n次独立重复实验的模型及二项分布.
7. 超几何分布:
一般地,在含有M件次品的N件产品中,任取n件,其中恰有X件次品,则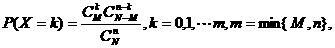 其中,
其中,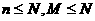 。
。
称分布列

X 0 1 … m
 P
P 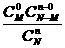
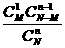 …
… 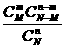
 为超几何分布列, 称X服从____________
为超几何分布列, 称X服从____________
答案: 超几何分布。
★ 重 难 点 突 破 ★
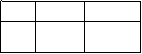
6. 两点分布:
 X 0 1
X 0 1
P 1-p p
特别提醒: 若随机变量X的分布列为两点分布, 则称X服从两点分布,而称P(X=1)为成功率.
5.离散型随机变量的二项分布:在一次随机试验中,某事件可能发生也可能不发生,在n次独立重复试验中这个事件发生的次数ξ是一个随机变量.如果在一次试验中某事件发生的概率是P,那么在n次独立重复试验中这个事件恰好发生k次的概率是
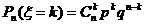 ,(k=0,1,2,…,n,
,(k=0,1,2,…,n,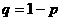 ).
).
于是得到随机变量ξ的概率分布如下:
|
ξ |
0 |
1 |
… |
k |
… |
n |
|
P |
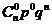 |
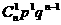 |
… |
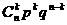 |
… |
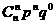 |
由于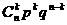 恰好是二项展开式
恰好是二项展开式
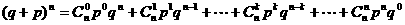
中的各项的值,所以称这样的随机变量ξ服从____________,
记作ξ-B(n,p),其中n,p为参数,并记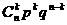 =b(k;n,p).
=b(k;n,p).
答案:二项分布
4.如果在1次试验中某事件发生的概率是P,那么在n次独立重复试验中这个事件恰好发生k次的概率计算公式:________________________
答案:Pn(k)=C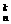 Pk(1-P)n-k,其中,k=0,1,2,…,n.
Pk(1-P)n-k,其中,k=0,1,2,…,n.
3.独立重复试验: 在同样的条件下,重复地、各次之间____________的一种试验.在这种试验中,每一次试验只有____________结果,即某事件要么发生,要么不发生,并且任何一次试验中发生的概率都是一样的.
答案: 相互独立地进行, 两种
2. 相互独立事件:如果事件A(或B)是否发生对事件B(或A)发生的概率没有影响,这样的两个事件叫做相互独立事件。
特别提醒:
①如果事件A、B是相互独立事件,那么,A与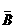 、
、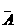 与B、
与B、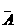 与
与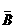 都是相互独立事件
都是相互独立事件
②两个相互独立事件同时发生的概率,等于每个事件发生的概率的积。我们把两个事件A、B同时发生记作A·B,则有P(A·B)= P(A)·P(B)
推广:如果事件A1,A2,…An相互独立,那么这n个事件同时发生的概率,等于每个事件发生的概率的积。即:P(A1·A2·…·An)= P(A1)·P(A2)·…·P(An)
1.条件概率:称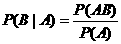 为在事件A发生的条件下,事件B发生的概率。
为在事件A发生的条件下,事件B发生的概率。
特别提醒:
①0 P(B|A)
P(B|A) 1;
1;
②P(B∪C|A)=P(B|A)+P(C|A)。
157.对于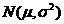 ,取值小于x的概率
,取值小于x的概率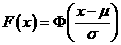 .
.
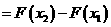
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com