
题目列表(包括答案和解析)
6、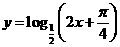 的单调递减区间是( )
的单调递减区间是( )
A、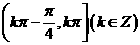 B、
B、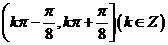
C、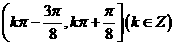 D、
D、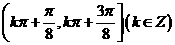
5、化简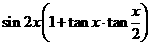 的结果为( )
的结果为( )
A、 B、
B、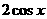 C、
C、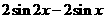 D、
D、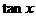
4、函数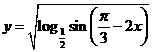 的定义域是( )
的定义域是( )
A、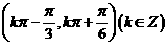 B、
B、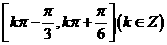
C、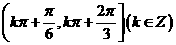 D、
D、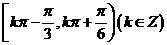
3、函数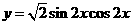 是( )
是( )
A、周期为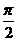 的奇函数
B、周期为
的奇函数
B、周期为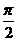 的偶函数
的偶函数
C、周期为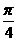 的奇函数
D、周期为
的奇函数
D、周期为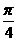 的偶函数
的偶函数
2、已知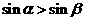 ,则下列命题正确的是( )
,则下列命题正确的是( )
A、若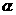 、
、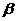 为第一象限角,则
为第一象限角,则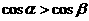
B、若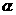 、
、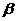 为第二象限角,则
为第二象限角,则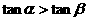
C、若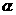 、
、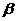 为第三象限角,则
为第三象限角,则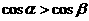
D、若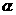 、
、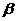 为第四象限角,则
为第四象限角,则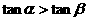
1、已知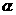 是第二象限角,
是第二象限角,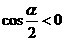 ,则
,则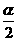 是( )
是( )
A、第一象限角 B、第二象限角 C、第三象限角 D、第四象限角
9. 已知三角函数值求角
(1)反正弦概念
反正弦的定义
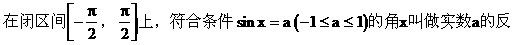

理解反正弦概念须注意以下几点:

arcsina无意义。
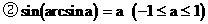
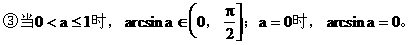
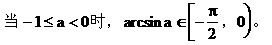
(2)反余弦概念
反余弦的定义
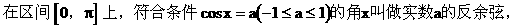
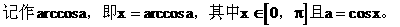
理解反余弦定义须注意:

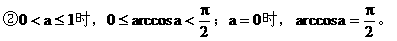
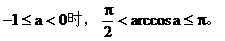
(3)反正切概念
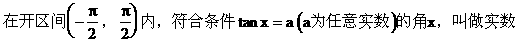

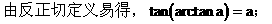
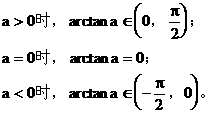
[典型例题]
例1. 试求函数y=sinx+cosx+2sinxcosx+2的最大值和最小值。
解: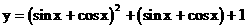
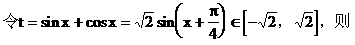
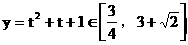
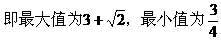
说明:本题主要通过换元将三角问题转化为代数问题。
例2. 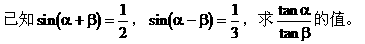
解: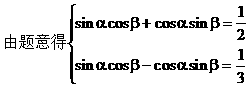
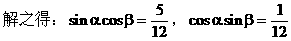
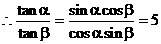
说明:本题关键是将sinαcosβ与cosαsinβ看成一个整体,通过解方程组而求解。
例3. 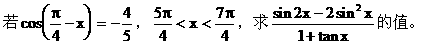
解: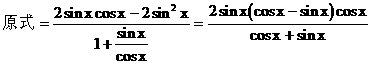
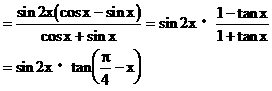
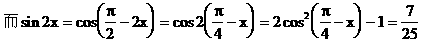
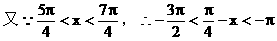
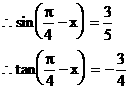
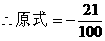
说明: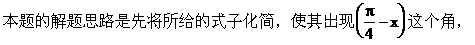
然后再求值。
例4. 
(1)求f(x)的最小正周期。
(2)求f(x)取得最值时x的值。
(3)求f(x)单调递增区间。
解: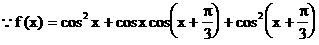
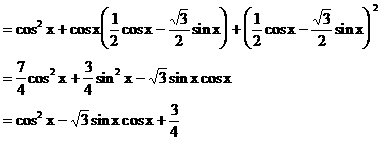
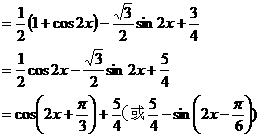
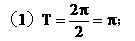
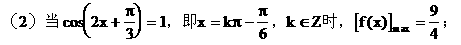
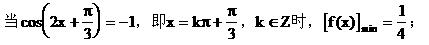
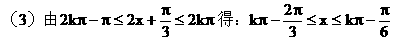
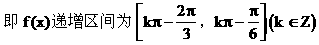
例5. 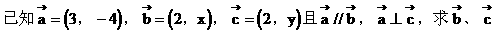

解: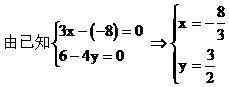
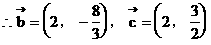
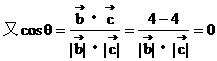
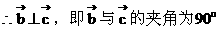
例6. 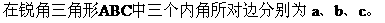
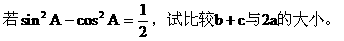
解: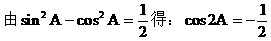
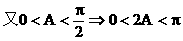
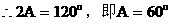
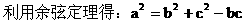
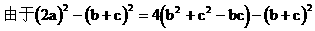
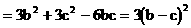
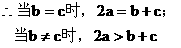
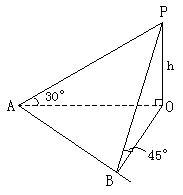
例7. 如图在地面上有一旗杆OP,为了测得它的高h,在地面上选一基线AB,AB=20m,在A点测得P点仰角∠OAP=30°,在B点测得P点的仰角∠OBP=45°,又测得∠AOB=60°,求旗杆的高度。
解: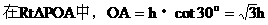
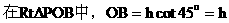
在△AOB中,运用余弦定理:
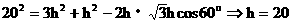
答:旗杆的高度为20m。
[复习测试]
7. 三角函数的图象和性质
[要点1]用“五点法”作图。五个特殊点。
[要点2]正弦函数、余弦函数性质。研究函数性质通常从五个方面研究:定义域、值域、单调性、奇偶性、周期性。
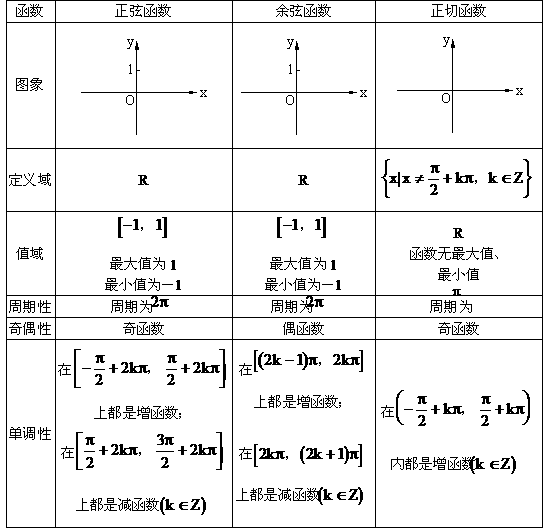
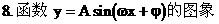
(1)五点法画图
(2)变换
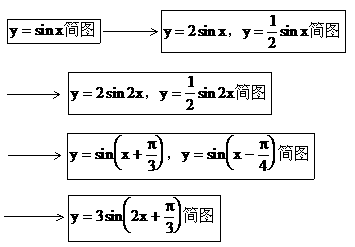
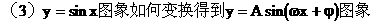
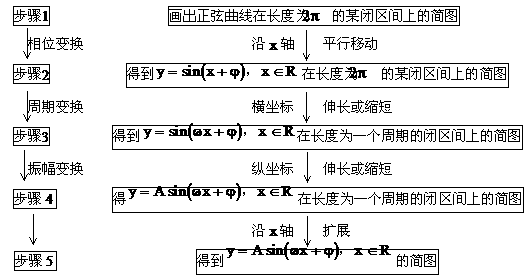
6. 两角和与差的正弦、余弦、正切
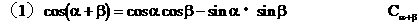
(2)变换α与β的取值及运用公式与同角三角函数关系式得:
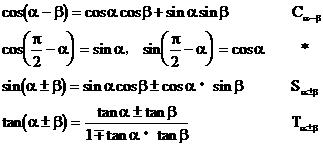
说明:(1)对于公式(*)初中要求α、β为锐角,事实上可以取任意角。
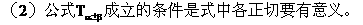
倍角公式:
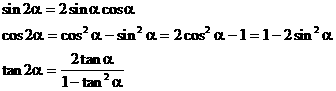
它们的内在联系及其推导线索如下:
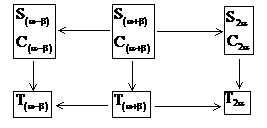
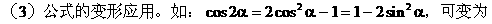
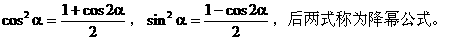
5. 诱导公式
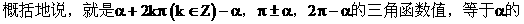
同名函数值,前面加上一个把α看成锐角时原函数值的符号。
此外,我们还证明了诱导公式
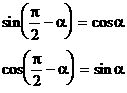
对于α为任意角都能成立。
(1)[0°,360°]间的角用[0°,90°]间的角表示。
若0°≤α≤90°,则[90°,180°]间的角可表示为180°-α。
[180°,270°]间的角可表示为180°+α,
[270°,360°]间的角可表示为360°-α。
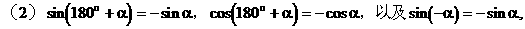
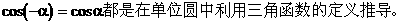
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com