
题目列表(包括答案和解析)
8.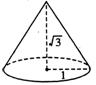 如图所示,圆锥的底面半径为1,高为
如图所示,圆锥的底面半径为1,高为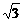 ,则圆锥的表面积为( )
,则圆锥的表面积为( )
A.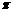 B.
B.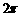 C.
C.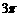 D.
D.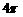
分析:设圆锥的母线长为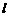 ,则
,则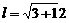 ,所以圆锥的表面积为
,所以圆锥的表面积为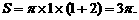
答案:C
7.已知某几何体的俯视图如图所示的矩形,正视图(或称主视图)是一个底边长为8,高为4的等腰三角形,侧视图(或称左视图)是一个底边长为6、高为4的等腰三角形。
(1)求该几何体的体积V;
(2)求该几何体的侧面积S。
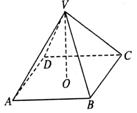 解:由三视图可知该几何体是一个底面边长分别为6、8的矩形,高为4的四棱锥。设底面矩形为ABCD。如图所示,
解:由三视图可知该几何体是一个底面边长分别为6、8的矩形,高为4的四棱锥。设底面矩形为ABCD。如图所示,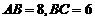 ,高
,高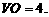
(1)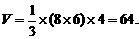
(2)设四棱锥侧面VAD、VBC是全等的等腰三角形,侧面VAB、VCD也是全等的等腰三角形,
在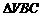 中,BC边上的高为
中,BC边上的高为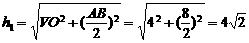 ,
,
在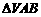 中,AB边上的高为
中,AB边上的高为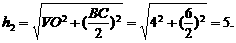
所以此几何体的侧面积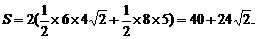
点评:高考试题中对面积和体积的考查有三种方式,一是给出三视图,求其面积或体积;二是与的组合体有关的面积和体积的计算;三是在解答题中,作为最后一问。
6.如果一个空间几何体的正视图与侧视图均为全等的等边三角形,俯视图为一个半径为1的圆及其圆心,那么这个几何体的体积为( )
A.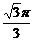 B.
B.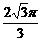 C.
C.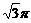 D.
D.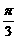
分析:由三视图知该几何体是圆锥,且轴截面是等边三角形,其边长等于底面直径2,则圆锥的高是轴截面等边三角形的高为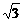 ,所以这个几何体的体积为
,所以这个几何体的体积为
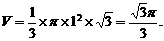
 答案:A
答案:A
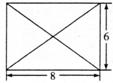
5.若一个正三棱柱的三视图如图所示,则这个正三棱柱的表面积为( )
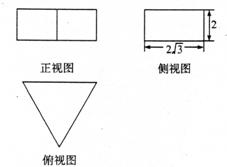
A.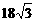 B.
B.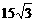 C.
C.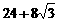 D.
D.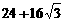
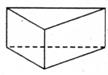 分析:该正三棱柱的直观图如图所示,且底面等边三角形的高为
分析:该正三棱柱的直观图如图所示,且底面等边三角形的高为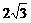 ,正三棱柱的高为2,则底面等边三角形的边长为4,所以该正三棱柱的表面积为
,正三棱柱的高为2,则底面等边三角形的边长为4,所以该正三棱柱的表面积为
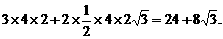
答案:C
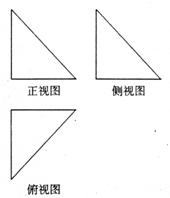
4.如图所示,一个空间几何体的正视图、侧视图、俯视图为全等的等腰直角三角形,如果直角三角形的直角边长为1,那么这个几何体的体积为( )
A.1 B.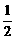 C.
C.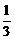 D.
D.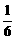
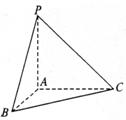 活动:让学生将三视图还原为实物图,讨论和交流该几何体的结构特征。
活动:让学生将三视图还原为实物图,讨论和交流该几何体的结构特征。
分析:根据三视图,可知该几何体是三棱锥,图中所示为该三棱锥的直观图,并且侧棱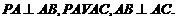 则该三棱锥的高是PA,底面三角形是直角三角形,所以这个几何体的体积为
则该三棱锥的高是PA,底面三角形是直角三角形,所以这个几何体的体积为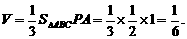
答案:D
点评:本题订考查几何体的三视图和体积,给出几何体的三视图,求该几何体的体积或面积时,首先根据三视图确定该几何体的结构特征,再利用公式求得,此类题目成为新课标高考的热点,应引起重视。
3.三棱锥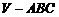 的中截面是
的中截面是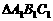 ,则三棱锥
,则三棱锥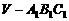 与三棱锥
与三棱锥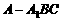 的体积之比是( )
的体积之比是( )
A.1:2 B.1:4 C.1:6 D.1:8
 分析:中截面将三棱锥的高分成相等的两部分,所以截面与原底面的面积之比为1:4,将三棱锥
分析:中截面将三棱锥的高分成相等的两部分,所以截面与原底面的面积之比为1:4,将三棱锥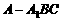 转化为三棱锥
转化为三棱锥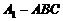 ,这样三棱锥
,这样三棱锥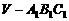 与三棱锥
与三棱锥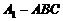 的高相等,底面积之比为1:4,于是其体积之比为1:4。
的高相等,底面积之比为1:4,于是其体积之比为1:4。
答案:B
2.两个平行于圆锥底面的平面将圆锥的高分成相等的三段,那么圆锥被分成的三部分的体积的比是( )
A.1:2:3 B.1:7:19 C.3:4:5 D.1:9:27
分析:因为圆锥的高被分成的三部分相等,所以两个截面的半径与原圆锥底面半径之比为1:2:3,于是自上而下三个圆锥的体积之比为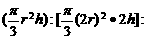
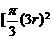 ·
·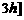
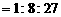 ,所以圆锥被分成的三部分的体积之比为
,所以圆锥被分成的三部分的体积之比为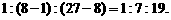
答案:B
1.已知圆柱和圆锥的高、底面半径均分别相等。若圆柱的底面半径为 ,圆柱侧面积为S,求圆锥的侧面积。
,圆柱侧面积为S,求圆锥的侧面积。
解:设圆锥的母线长为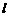 ,因为圆柱的侧面积为S,圆柱的底面半径为
,因为圆柱的侧面积为S,圆柱的底面半径为 ,即
,即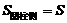 ,根据圆柱的侧面积公式可得:圆柱的母线(高)长为
,根据圆柱的侧面积公式可得:圆柱的母线(高)长为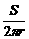 ,由题意得圆锥的高为
,由题意得圆锥的高为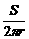 ,又圆柱的底面半径为
,又圆柱的底面半径为 ,根据勾股定理,圆锥的母线长
,根据勾股定理,圆锥的母线长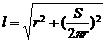 ,根据圆锥的侧面积公式得
,根据圆锥的侧面积公式得
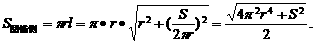
4.圆台的上、下底面半径分别为2,4,母线长为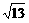 ,则这个圆台的体积V= 。
,则这个圆台的体积V= 。
3.长、宽、高分别为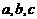 的长方体的表面积S= 。
的长方体的表面积S= 。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com