
题目列表(包括答案和解析)
4.棱锥定义:
3.棱柱定义:
2.点动成 , 动成面,面动成 ;
1. 平面的三个性质 、 , ;
4.要注意集合语言与其他数学语言互译的准确性
事实上,各种数学语言形态间的互译,可为我们在更广阔的思维领域里寻找问题的解决途径,因而这种互译是我们在解题过程中常常必须做的事情。
对于用集合语言叙述的问题,求解时往往需要转译成一般的代数语言或几何语言。
[例]已知集合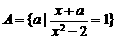 有唯一实数解,用列举法表示集合A。
有唯一实数解,用列举法表示集合A。
解:集合A表示方程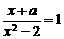 ①
①
即方程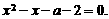 ②
②
有等根时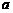 的取值集合。
的取值集合。
方程②有等根的条件是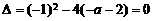 ,
,
解得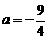 .因此
.因此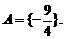
以上解法对吗?为什么?
[解析]不对,不难看出,将A转译为方程②有等根时,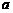 的取值集合是不准确的。
的取值集合是不准确的。
转译时忽视了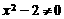 ,即
,即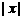
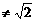 这一隐含条件。可见,与方程①等价的应是混合组
这一隐含条件。可见,与方程①等价的应是混合组
|
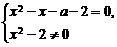
因此,在讨论方程②有唯一实根时,必须照顾到③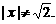 由于方程①为分式方程,可能有增根,当条件②的两实根中有一个是方程①的增根
由于方程①为分式方程,可能有增根,当条件②的两实根中有一个是方程①的增根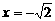 或
或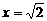 时,方程也只有一个实根,正确解法是:
时,方程也只有一个实根,正确解法是:
方程①等价于混合组。
(1)当②有等根时,同上解得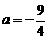 ,此时
,此时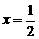 ,适合③;
,适合③;
(2)当②有两个不等的实根时,由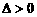 ,可得
,可得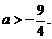
当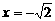 为①的增根时,由②得
为①的增根时,由②得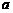
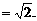
当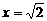 为①的增根时,由②得
为①的增根时,由②得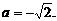
∵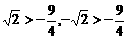 ,
,
∴由(1)、(2)得
[点评]集合语言转译成其他语言,转译的准确与否直接关系到解题的成功与失败。集合语言与其他语言转译过程中,根据问题的需要也可能转译成图形语言,利用数形结合解题,根据解题需要,有时也可能将其他语言转译为集合语言。
3.要注意空集的特殊性和特殊作用
空集是一个特殊的重要集合,它不含任何元素,是任何集合的子集,是任何非空集合的真子集。显然,空集与任何集合的交集为空集,与任何集合的并集仍等于这个集合。当题设中隐含有空集参与的集合关系时,其特殊性是很容易被忽视的,从而引发解题失误。
[例]已知集合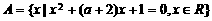 ,
,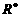 为正实数集合,若
为正实数集合,若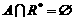 ,求
,求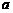 的取值范围。
的取值范围。
[解析]由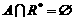 知A中元素为非正数,即方程
知A中元素为非正数,即方程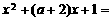 0没有正解。
0没有正解。
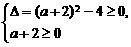 解得
解得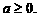
上面这个结果是不完整的,上述的解答只注意到A为非空集合的情形,当A为空集时仍满足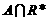 =
=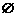 。
。
此时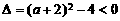 ,解得
,解得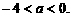
综合以上两种情况可得
[点评]从以上解答应看到:解决有关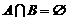 、
、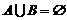 、
、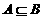 等集合问题易忽视空集的情况而出现漏解。这需要在解题过程中要全方位、多角度审视问题。
等集合问题易忽视空集的情况而出现漏解。这需要在解题过程中要全方位、多角度审视问题。
2.充分注意集合元素的互异性
集合元素的互异性,是集合的重要属性,教学实践告诉我们,集合中元素的互异性常常被学生在解题中所忽略,从而导致解题的失败,下面再结合例题进一步讲解以强化对集合元素互异性的认识。
[例]若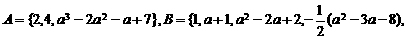
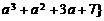 且
且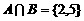 ,试求实数
,试求实数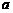 的值。
的值。
[解析]∵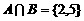 ,∴
,∴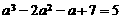 ,由此求得
,由此求得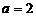 或
或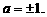
至此不少学生认为大功告成,事实上,这只是保证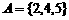 ,集合B中的元素是什么,它是否满足元素的互异性,有待于进一步考查。
,集合B中的元素是什么,它是否满足元素的互异性,有待于进一步考查。
当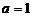 时,
时,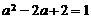 ,与元素的互异性相违背,故应舍去
,与元素的互异性相违背,故应舍去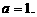
当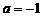 时,
时,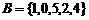 ,与
,与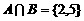 相矛盾,故又舍去
相矛盾,故又舍去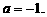
当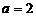 时,
时,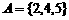 ,
,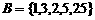 ,此时
,此时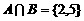 ,满足。
,满足。
∴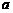 =2为所求。
=2为所求。
[点评]集合中的这类问题求解都要注意检验,使其舍去不合条件的解。
1.要注意正确理解运用集合概念
把集合作为一种数学语言,以表达一定范围或具有某些特性的元素。例如,方程(或方程组)的解集,不等式(或不等式组)的解集,具有某种性质或满足某些条件的数集、点集、向量集(以后会学)等,因集合元素的任意性,使得集合语言有着广泛的应用性。
[例](1)已知集合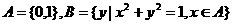 ,则A与B的关系为( )
,则A与B的关系为( )
A.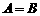 B.
B.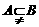 C.
C.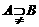 D.
D.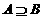
(2)已知集合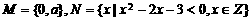 ,若
,若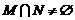 ,则
,则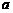 为( )
为( )
A.1 B.2 C.1或2 D.不为零的任意实数
[解析](1)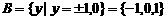 ∴
∴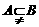 .选B。
.选B。
(2)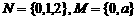 ,∵
,∵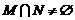 .
.
∴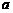 取不为零的任意实数,故选D。
取不为零的任意实数,故选D。
10.奇偶性的判断步骤:(1)称求函数的定义域,若定义域关于坐标原点对称,继续以下步骤,若不对称,则为非奇非偶函数;(2)计算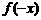 的值;(3)判断
的值;(3)判断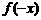 与
与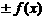 中的哪一个相等;(4)下结论。
中的哪一个相等;(4)下结论。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com