
题目列表(包括答案和解析)
10.给出下列说法:
①函数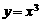 的图象关于原点成中心对称;
的图象关于原点成中心对称;
②函数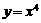 的图象关于y轴成轴对称;
的图象关于y轴成轴对称;
③函数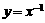 在
在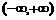 上是减函数.
上是减函数.
其中正确说法的个数是( )
A.0 B.1 C.2 D.3
9.函数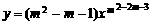 是幂函数,且
是幂函数,且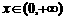 时为减函数,则实数m的值为( )
时为减函数,则实数m的值为( )
A.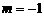 或2 B.
或2 B.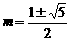 C.
C.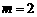 D.
D.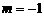
8.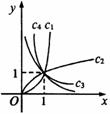 图中曲线是幂函数
图中曲线是幂函数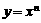 在第一象限内的图象,已知n取
在第一象限内的图象,已知n取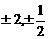 四个值,则相应曲线
四个值,则相应曲线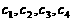 的n值依次为( )
的n值依次为( )
A.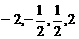 B.
B.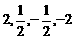
C.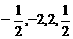 D.
D.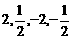
7.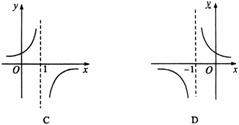
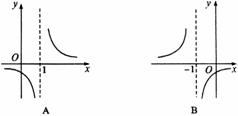
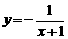 的图象是( B )
的图象是( B )
6.当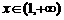 时,下列函数的图象全在直线
时,下列函数的图象全在直线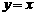 下方的偶函数是( )
下方的偶函数是( )
A.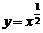 B.
B.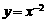 C.
C.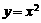 D.
D.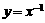
5.如图所示,幂函数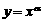 在第一象限的图象,比较0,
在第一象限的图象,比较0,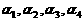 ,1的大小( )
,1的大小( )
 A.
A.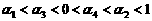
B.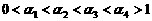
C.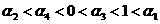
D.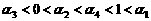
4.下列函数中是幂函数的为( )
①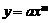 (a、m为非零常数,且
(a、m为非零常数,且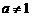 );②
);②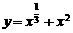 ;③
;③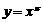 ;④
;④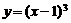
A.①③④ B.③ C.③④ D.全不是
3.在函数y=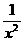 ,y=2x3,y=x2+x,y=1中,幂函数有( )
,y=2x3,y=x2+x,y=1中,幂函数有( )
A.0个 B.1个 C.2个 D.3个
1.使x2>x3成立的x的取值范围是( )
A.x<1且x≠0 B.0<x<1
C.x>1 D.x<1
 2.若四个幂函数y=
2.若四个幂函数y=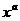 ,y=
,y=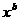 ,y=
,y=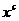 ,y=
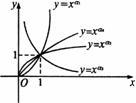
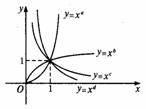
,y= 在同一坐标系中的图象如右图,则a、b、c、d的大小关系是( )
在同一坐标系中的图象如右图,则a、b、c、d的大小关系是( )
A.d>c>b>a
B.a>b>c>d
C.d>c>a>b
D.a>b>d>c
[考题1]作出函数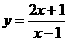 的图象,并指出此函数的定义域、值域,若此函数的图象是中心对称图形,则指出它的对称中心的坐标。
的图象,并指出此函数的定义域、值域,若此函数的图象是中心对称图形,则指出它的对称中心的坐标。
[解析]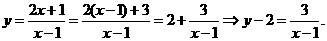
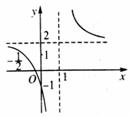 则
则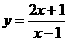 可以看做是将函数
可以看做是将函数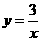 的图象向右平移一个单位后再向上平移2个单位,如图。
的图象向右平移一个单位后再向上平移2个单位,如图。
定义域为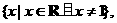
值域为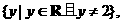
对称中心为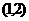 .
.
[点评]对于函数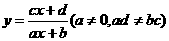 ,它的图象是双曲线,它的两条渐近线方程分别为
,它的图象是双曲线,它的两条渐近线方程分别为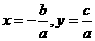 ,对称中心为
,对称中心为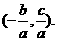 这个结论非常有价值,例如,我们要作
这个结论非常有价值,例如,我们要作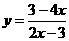 的图象,两条渐近线
的图象,两条渐近线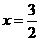 ,
,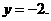 再用一点
再用一点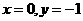 确定双曲线的位置即可作出
确定双曲线的位置即可作出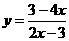 的草图。
的草图。
[考题2](1)在如图所示的函数图象中,表示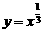 的是( )
的是( )
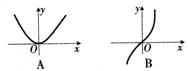
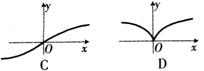
[解析]函数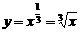 是奇函数,图象在第一、三象限,且
是奇函数,图象在第一、三象限,且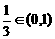 ,所以在第一象限的图象向上凸,故选C。
,所以在第一象限的图象向上凸,故选C。
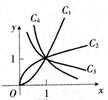 (2)如图,幂函数
(2)如图,幂函数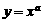 在第一象限内的图象,已知
在第一象限内的图象,已知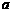 取
取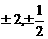 四个值,则相应于曲线
四个值,则相应于曲线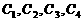 的
的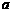 依次为( )
依次为( )
A.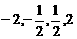 B.
B.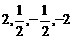
C.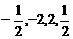 D.
D.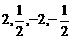
[分析]根据幂函数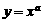 在第一象限内的图象特征,在区间
在第一象限内的图象特征,在区间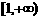 上,当
上,当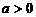 时,
时,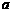 越大,
越大,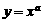 的增长速度就越快,所以
的增长速度就越快,所以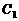 的
的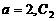 的
的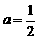 .在区间
.在区间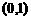 上,当
上,当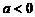 ,
,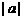 越大,图象越陡峭。所以
越大,图象越陡峭。所以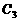 的
的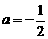 ,
,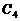 的
的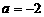 .故选B。
.故选B。
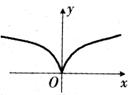
(3)如图所示是函数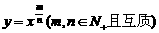 的图象,则( )
的图象,则( )
 A.
A.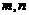 是奇数,且
是奇数,且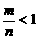
B. 是偶数,
是偶数,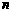 是奇数,且
是奇数,且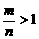
C. 是偶数,
是偶数,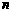 是奇数,且
是奇数,且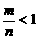
D.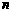 是偶数,
是偶数, 是奇数,且
是奇数,且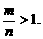
分析:由图象在第一象限的特点,知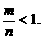 又由函数图象关于
又由函数图象关于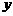 轴对称,知
轴对称,知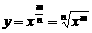 是偶函数,所以
是偶函数,所以 是偶数,
是偶数,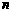 是奇数。故选C。
是奇数。故选C。
[考题3]已知函数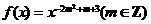 为偶函数,且
为偶函数,且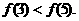
(1)求 的值,并确定
的值,并确定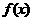 的解析式;
的解析式;
(2)若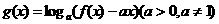 ,是否存在实数
,是否存在实数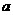 ,使
,使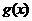 在区间[2,3]上为增函数。
在区间[2,3]上为增函数。
[分析]问题的解决往往依赖于对条件或结论的转化,对于(1),应首先转化较为复杂的条件,如果从偶函数的角度开始转化,不论是用偶函数的定义还是用幂函数中的偶函数,都难以找到进一步转化的途径,但从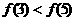 入手,就不难把转化继续进行下去,对于(2),对于(1)中没有附加的条件,因而可以利用(1)的结论转化(2)的附加条件,并利用单调函数的性质使问题得到解决。
入手,就不难把转化继续进行下去,对于(2),对于(1)中没有附加的条件,因而可以利用(1)的结论转化(2)的附加条件,并利用单调函数的性质使问题得到解决。
[解析](1)由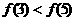 得
得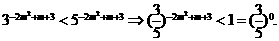
∵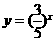 在
在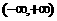 上为减函数,
上为减函数,
∴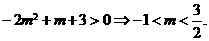
∵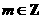 ,∴
,∴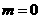 或
或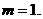
当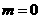 时,
时,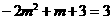 ;
;
当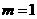 时,
时,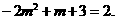
而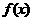 为偶函数,∴
为偶函数,∴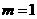 ,此时
,此时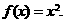
(2)假设存在实数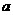 ,使
,使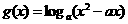 在区间
在区间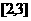 上为增函数。
上为增函数。
则由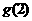 与
与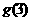 存在,得
存在,得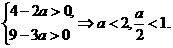
令 ,则
,则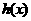 开口向上,对称轴
开口向上,对称轴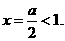
∴当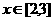 ,
,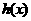 为增函数,又由
为增函数,又由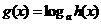 在区间
在区间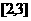 上为增函数,得
上为增函数,得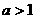 ,∴
,∴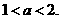
[点评]该题亦可分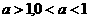 两种情况讨论求解。
两种情况讨论求解。
[考题4](1)求下列函数的定义域和值域。
①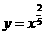 ;②
;②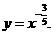
[解析]①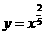 的定义域为实数集
的定义域为实数集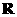 ,值域为
,值域为 .
.
②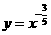 的定义域为
的定义域为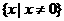 ,值域为
,值域为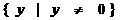
(2)函数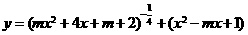 的定义域是全体实数,则实数
的定义域是全体实数,则实数 的取值范围是( )
的取值范围是( )
A.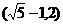 B.
B.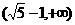
C.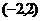 D.
D.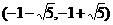
[解析]函数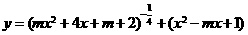 有意义的条件是
有意义的条件是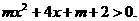
因此,要使函数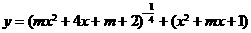 的定义域为全体实数,需满足
的定义域为全体实数,需满足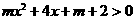 对一切实数都成立。
对一切实数都成立。
即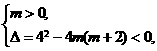 解得
解得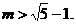
∴选B。
[点评]幂函数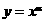 的定义域和值域也是与
的定义域和值域也是与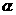 的取值密切相关,
的取值密切相关,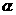 的正负和分母的奇偶都是制约
的正负和分母的奇偶都是制约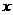 的取值范围的因素,因此要具体情况具体分析,或结合图象的位置与形状加以考虑。
的取值范围的因素,因此要具体情况具体分析,或结合图象的位置与形状加以考虑。
[考题5]已知函数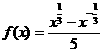 ;
;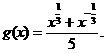
(1)证明: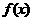 是奇函数,并求
是奇函数,并求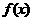 的单调区间;
的单调区间;
(2)分别计算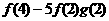 和
和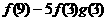 的值,由此概括出涉及函数
的值,由此概括出涉及函数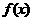 和
和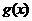 对所有不等于零的实数
对所有不等于零的实数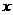 都成立的一个等式,并加以证明。
都成立的一个等式,并加以证明。
[解析](1)函数定义域为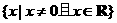 ,
,
∵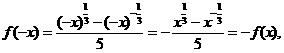
∴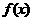 为奇函数,
为奇函数,
设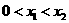 ,则
,则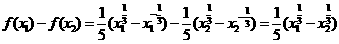
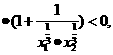
∴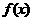 在
在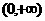 上是增函数,又
上是增函数,又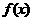 是奇函数.
是奇函数.
∴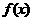 在
在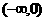 上也是增函数.
上也是增函数.
故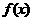 在
在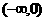 和
和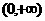 上单调递增.
上单调递增.
(2)解: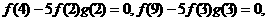
猜想: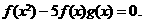
∵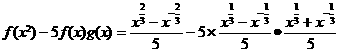
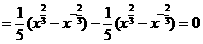 ,
,
∴等式成立。
[考题6]比较下列各组数的大小;
(1)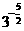 和
和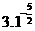 ;(2)
;(2)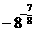 和
和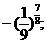
(3)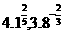 和
和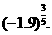
[解析]第(1)组可利用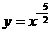 的单调性比较,第(2)组可利用
的单调性比较,第(2)组可利用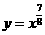 的单调性比较,第(3)组可利用
的单调性比较,第(3)组可利用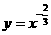 的单调性比较。
的单调性比较。
(1)函数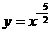 在
在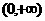 上为减函数,又
上为减函数,又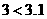 ,所以
,所以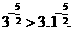
(2)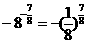 ,函数
,函数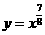 在
在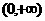 上为增函数,又
上为增函数,又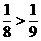 ,则
,则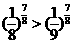 ,从而
,从而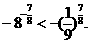
(3)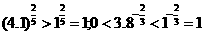 ;
;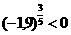 ;
;
所以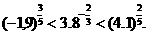
[点评]比较大小题,要综合考虑函数的性质,特别是单调性的应用,更善于运用“搭桥”法进行分组,常数0和1是常用的参数。
[考题7]若 ,试求
,试求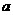 的取值范围。
的取值范围。
[分析]由函数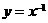 的图象及单调性可解.
的图象及单调性可解.
[解析]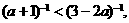
∴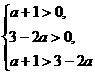 或
或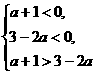 或
或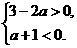
解得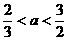 或
或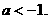
[点评]考虑要全面,谨防考虑不周导致误解。
[考题8]若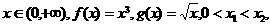
求证:(1)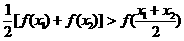 ;
;
(2)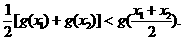
[证明](1)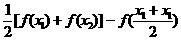
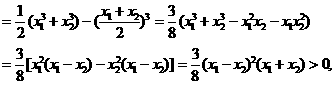
∴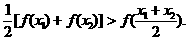
(2)∵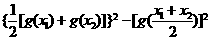
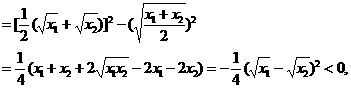
∴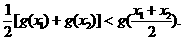
[点评]本题即凸凹函数的一个重要性质,从图形上可体现出来.
[考题9]某工厂从1949年的年产值100万元增加到40年后1989年的500万元,如果每年年增长率相同,则每年年产值增长率是多少?
[解析]自然对数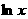 是以
是以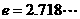 为底的对数,本题中增长率
为底的对数,本题中增长率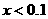 ,可用自然对数的近似公式
,可用自然对数的近似公式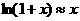 ,取
,取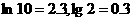 来计算。
来计算。
解法一:设每年年产值增长率为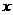 ,
,
根据题意,有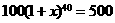 ,即
,即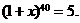
两边取自然对数,得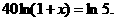
又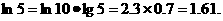
利用已知条件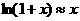
得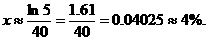
解法二:同解法一,列出关系式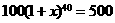 ,即
,即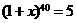 ,两边取常用对数,得
,两边取常用对数,得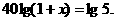
∴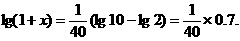
由换底公式,得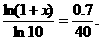
由已知条件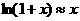 得
得
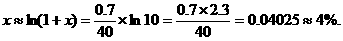
答:每年的年产值增长率为4%。
[点评]若没有条件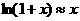 ,可用计算器直接计算。
,可用计算器直接计算。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com