2、通过对数函数的性质应用，进一步理解对数函数性质

1、结合函数的定义域和值域加深对对数函数和性质的认识。

3、已知f(x)满足f(x² – 3) = log₆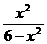(a > 0且a≠1)

(1)求f(x)的解析式；

(2)判断f(x)的奇偶性；

(3)讨论f(x)的单调性.

高一年级数学导学提纲

对数函数(3)

执笔人：徐江梅　 审核人：纪尧兵

复习目标：

2、若log_a(a² + 1) < log_a2a < 0，那么a的取值范围为　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

A　 (0，1)　　　　　　　　　　 B　 (0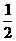，)　　　　　　　　　 C　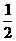 (，1)　　　　　　　　　 D　 (1，+∞)

备用练习：对数函数(二)

1、方程log₂(x + 4) = 2^x的实数解的个数为　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　 )

A　 0　　　　　　　　　　　　　　　　　　 B　 1　　　　　　　　　　　　　　　　　　 C　 2　　　　　　　　　　　　　　　　　　 D　 3

例1、探究函数y=log₃(x+2)的图象与函数y=log₃x的图象间的关系

思考：函数y=log_a(x+b)与函数y=log_ax(a>0且a≠1,b≠0)的图象之是有什么关系？

例2、画出函数y = log₂|x|的图象，并根据图象写出它的单调区间。

2、练习

(1)P70　　　　 第1到8题

(2)方程a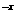= log_ax(a > 0且a≠1)的实数解个数是　　　　　　　　　　　　　　　　　　　　 (　　 )

A　 0个　　　　　　　　　　　　　　　 B　 1个　　　　　　　　　　　　　　　 C　 2个　　　　　　　　　　　　　　　 D　 3个

(3)函数f(x) = log₂(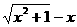)是　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 (　　 )

A　 奇函数　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　　 B　 偶函数　　　　　　　　　　　　

C　 既奇函数又偶函数　　　　　　　　　　　　　　　　　　　　　　　　 D　 非奇非偶函数

(4)函数y = log_ax在[2，10]上的最大值与最小值的差为1，则常数a = 　　　　　　　　　　　　

(1)如何由函数y=2^x的图象得到函数y=2^x+a的图象，以及函数y=2^x+b的图象？

(2)以上变化规律对于对数函数是否也运用？

2、对数函数的特性以及函数的通性在解决有关问题中的应用

教学难点

会有对数式的较为复杂的函数的单调性和奇偶性的判断和证明

教学过程

1、函数图象的平移和翻转变化

2、能运用函数的通性通讯对数函数的特征，讨论研究会有对数式的复合函数的性质

教学重点