
题目列表(包括答案和解析)
4.已知不恒为零的函数f(x)对任意实数x、y满足f(x+y)+f(x-y)=2[f(x)+f(y)],则函数f(x)是( )
(A)奇函数非偶函数 (B)偶函数非奇函数
(C)既是奇函数又是偶函数 (D)非奇非偶函数
3、.已知函数f(x)对一切实数x、y满足:f(0)≠0,
f(x+y)=f(x)f(y),且当x<0时,f(x)>1,则当x>0时,f(x)的取值范围是( )
(A)(1,+∞) (B)(-∞,1)
(C)(0,1) (D)(-1,+∞)
2. 若对任意实数x、y总有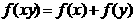 ,则下列各式中错误的是( )
,则下列各式中错误的是( )
(A)f(1)=0
(B)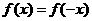
(C)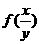 = f(x)-f(y)
(D)
= f(x)-f(y)
(D)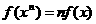 (n∈N)
(n∈N)
1.已知: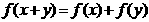 对任意实数
对任意实数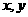 都成立,则( )
都成立,则( )
(A)f(0)=0 (B)f(0)=1
(C)f(0)=0或1 (D)以上都不对
[例1]已知函数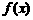 对任意
对任意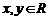 ,总有
,总有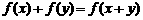 ,且当
,且当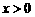 时,
时,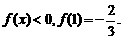
(1)求证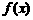 在R上是减函数;
在R上是减函数;
(2)求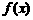 在
在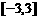 上的最大值和最小值。
上的最大值和最小值。
[解析](1)令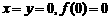 ,令
,令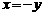 可得
可得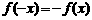 ,
,
在R上任取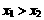
则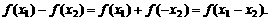
∵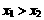 ,∴
,∴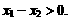
又∵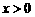 时,
时,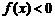 ,∴
,∴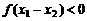 ,
,
即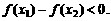
同定义可知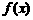 在R上为单调递减函数。
在R上为单调递减函数。
(2)∵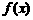 在R上是减函数,∴
在R上是减函数,∴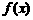 在
在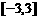 上也是减函数。
上也是减函数。
∴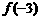 最大,
最大,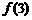 最小。
最小。
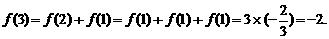
∴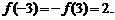
即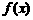 在
在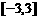 上最大值为2,最小值为
上最大值为2,最小值为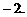
[点评]抽象函数的性质要紧扣定义,并同时注意特殊值的应用。
[例2]已知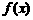 的定义域为R,对任意
的定义域为R,对任意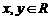 ,有
,有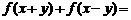
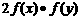 ,且
,且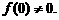
(1)求证: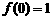 ;
;
(2)求证: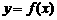 为偶函数。
为偶函数。
[解析](1)由题意得: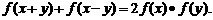
令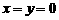 ,则
,则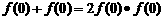 ,则
,则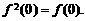
∵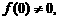 ∴
∴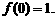
(2)令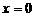 ,则
,则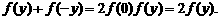
∴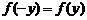 . ∴函数
. ∴函数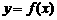 是偶函数。
是偶函数。
[点评]对于这类问题的求解,充分运用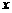 、
、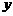 为任意实数这一条件,对
为任意实数这一条件,对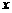 、
、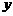 取定一些特殊值,如
取定一些特殊值,如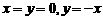 等。
等。
[例3]、定义在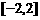 上的偶函数
上的偶函数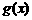 ,当
,当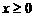 时,
时,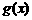 单调递减,若
单调递减,若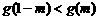 成立,求
成立,求 的取值范围。
的取值范围。
[解]因为函数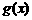 在
在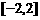 上是偶函数,
上是偶函数,
则由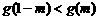 ,
,
可得到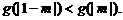
因为偶函数图象关于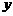 轴对称,
轴对称,
所以有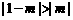 .又当
.又当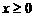 时,
时,
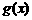 单调递减,得到
单调递减,得到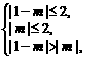 解之得
解之得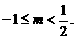
[点评]利用偶函数这一特性解决有关抽象函数的问题可以避免分类讨论。
[例题4]函数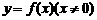 是奇函数,且当
是奇函数,且当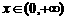 时是增函数,若
时是增函数,若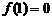 ,求不等式
,求不等式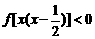 的解集。
的解集。
[分析]注意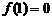 ,不等式可转化为
,不等式可转化为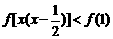 ,联系
,联系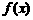 在
在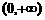 上递增,不难得出
上递增,不难得出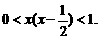
还要注意,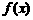 是奇函数,它在对称区间上的单调性相同,且
是奇函数,它在对称区间上的单调性相同,且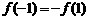 =0,于是又得
=0,于是又得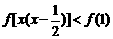 ,即
,即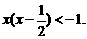
分别解两个不等式即可。
[解析]解不等式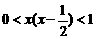 ,得
,得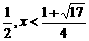 或
或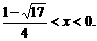
解不等式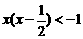 ,得
,得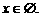
∴原不等式的解集是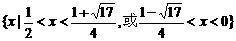
[点评]在关于原点对称的两个区间上,奇函数的单调性相同,偶函数的单调性相反。
到目前为止常见抽象函数与我们已学过的具体函数的对应关系如下表:
|
抽象函数模型 |
具体函数模型(举其中一例) |
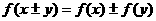 |
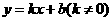 |
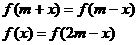 |
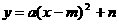 |
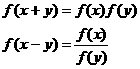 |
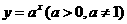 |
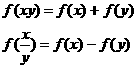 |
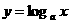 ,( ,(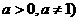 |
(三)、|同步练习:
1.设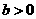 ,二次函数
,二次函数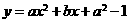 的图象为下列之一:
的图象为下列之一:
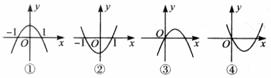
则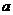 的值为( )
的值为( )
A.1 B.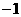 C.
C.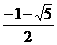 D.
D.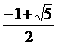
[解析]∵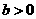 ,∴图象①②不可能,又③④过原点O,∴
,∴图象①②不可能,又③④过原点O,∴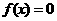 ,即
,即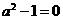 ,故
,故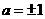 ,又
,又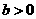 ,如果
,如果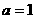 ,则
,则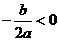 ,与③④图象矛盾. ∴
,与③④图象矛盾. ∴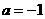 ,故选B。
,故选B。
2.方程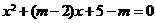 的两根都大于2,则
的两根都大于2,则 的取值范围是( )
的取值范围是( )
A.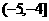 B.
B.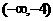 C.
C.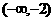 D.
D.
[解析]令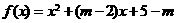 要使
要使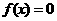 的两根都大于2,则
的两根都大于2,则
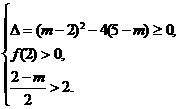
解得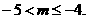
故选A。
3、已知关于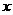 的方程
的方程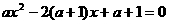 ,探究
,探究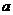
为何值时(1)方程有一根(2)方程有一正一负两根(3)两根都大于1(4)一根大于1一根小于1
答案:(1)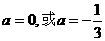 (2)
(2)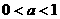 (3)无解(4)
(3)无解(4)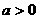
4、若关于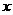 的方程
的方程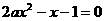 在(0,1)内恰有一解,求实数
在(0,1)内恰有一解,求实数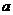 的取值范围。。
的取值范围。。
答案: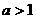
5、已知二次函数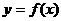 的两个零点
的两个零点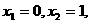 且其图象的顶点恰好在
且其图象的顶点恰好在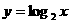 的图象上。
的图象上。
(1)求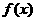 的解析式。
的解析式。
(2)设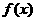 在
在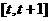 的最小值为
的最小值为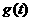 ,求
,求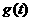 的表达式
的表达式
答案:(1)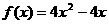
(2)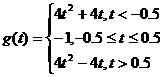
6.设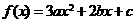 ,若
,若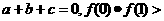 0,求证:
0,求证:
(1)方程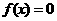 有实根;
有实根;
(2)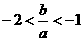 ;
;
(3)设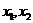 是方程
是方程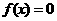 的两个实根,则
的两个实根,则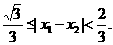
[解析](1)若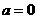 ,则
,则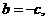
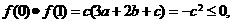
与已知矛盾,
∴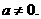
方程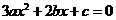 的判别式
的判别式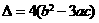 ,
,
由条件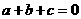 ,消去
,消去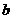 ,得
,得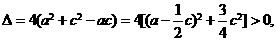
故方程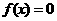 有实根.
有实根.
(2)由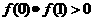 ,得
,得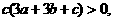
由条件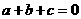 ,消去
,消去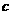 ,得
,得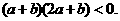
∵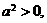
∴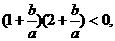
故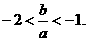
(3)由条件,知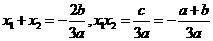 ,
,
∴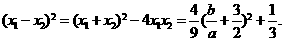
∵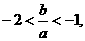
∴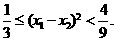
故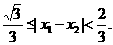
7.已知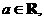 二次函数
二次函数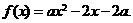 设不等式
设不等式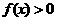 的解集为A,又知集合
的解集为A,又知集合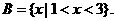 若
若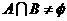 ,求
,求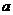 的取值范围。
的取值范围。
[解析]由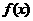 为二次函数
为二次函数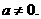
令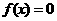 解得其两根为
解得其两根为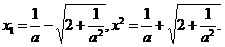
由此可知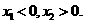
(1)当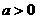 时,
时,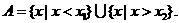
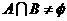 的充要条件是
的充要条件是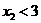 ,即
,即
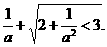
解得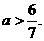
(2)当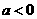 时,
时,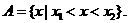
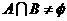 的充要条件是
的充要条件是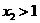 ,即
,即
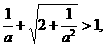
解得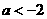 .
.
综上,使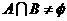 成立的
成立的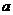 的取值范围为
的取值范围为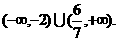
8、(1)求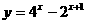 的值域
的值域
(2)关于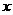 的
的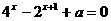 方程有解,求实数的
方程有解,求实数的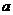 范围。
范围。
解析:本题是可转化为二次函数区间最值问题的题目。
答案:(1)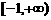 (2)
(2)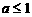
第五篇、抽象函数问题
一 定义:是指概括总结出一类函数所具有的共同特性,而没有给出具体的解析式(或图象)的一类函数,中学阶段的抽象函数,一般是以所学的基本函数为背景,概括其共同的本质特征而形成的。因此,在学习中要注意总结概括基本函数的共同特征,从特殊到一般,从具体到抽象,建立抽象函数与具体函数的对应关系。
例1、求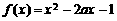 在区间
在区间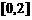 上的最大值和最小值。
上的最大值和最小值。
[分析]解决这类问题的关键是判别函数的定义域各区间上的单调性,再利用函数的单调性解决问题。
[解析]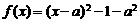 ,对称轴为
,对称轴为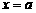 .
.
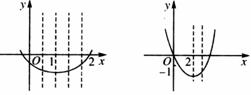
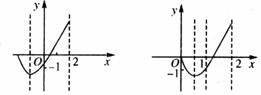 (1)当
(1)当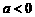 时,由图(1)可知,
时,由图(1)可知,
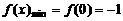 ,
,
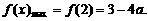
(1) (2)
(2)当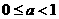 时,由图(2)可知,
时,由图(2)可知,
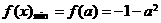 ,
,
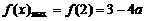
(3)当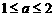 时,由图(3)可知,
时,由图(3)可知,
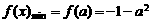 ,
,
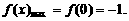
(3) (4)
(4)当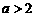 时,由图(4)可知,
时,由图(4)可知,
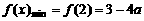 ,
,
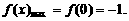
[点评](1)利用单调性求最值或值域应先判断函数在给定区间上的单调性。
(2)求解二次函数在某区间上的最值,应判断它的开口方向、对称轴与区间的关系,若含有字母应注意分类讨论,解题时最好结合图象解答。
例2、已知函数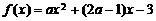 在区间
在区间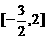 上的最大值为1,求实数
上的最大值为1,求实数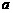 的值。
的值。
[解析]首先应搞清二次项系数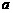 是否为零,如果
是否为零,如果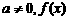 的最大值与二次函数系数
的最大值与二次函数系数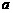 的正负有关,也与对称轴
的正负有关,也与对称轴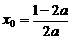 的位置有关,解答时必须用讨论法。
的位置有关,解答时必须用讨论法。
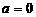 时,
时,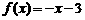 ,
,
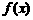 在
在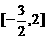 上不能取得1,故
上不能取得1,故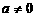 .
.
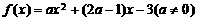 的对称轴方程为
的对称轴方程为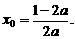
(1)令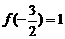 ,解得
,解得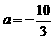 ,
,
此时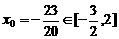 ,
,
因为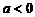 ,
,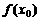 最大,所以
最大,所以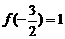 不合适。
不合适。
(2)令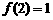 ,解得
,解得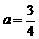 ,
,
此时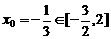 ,
,
因为 ,且距右端点2较远,所以
,且距右端点2较远,所以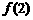 最大,合适。
最大,合适。
(3)令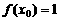 ,得
,得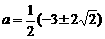 ,
,
验证后知只有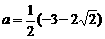 才合适。
才合适。
综上所述,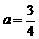 ,或
,或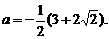
[点评]这里函数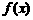 的最大值一是与
的最大值一是与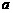 的符号有关。另外也与对称轴和区间的端
的符号有关。另外也与对称轴和区间的端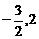 的远近有关,不分情况讨论就无法确定
的远近有关,不分情况讨论就无法确定
例3、(1)关于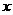 的方程
的方程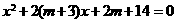 有两个实根,且一个大于1,一个小于1,求
有两个实根,且一个大于1,一个小于1,求 的取值范围;
的取值范围;
(2)关于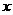 的方程
的方程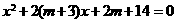 有两实根,在
有两实根,在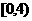 内,求
内,求 的取值范围;
的取值范围;
(3)关于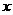 的方程
的方程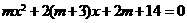 有两实根,且一个大于4,一个小于4,求
有两实根,且一个大于4,一个小于4,求 的取值范围.
的取值范围.
[解析](1)令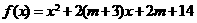 ,∵对应抛物线开口向上,∴方程有两个实根,且一个大于1,一个小于1等价于
,∵对应抛物线开口向上,∴方程有两个实根,且一个大于1,一个小于1等价于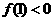 (思考:需要
(思考:需要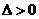 吗?),即
吗?),即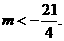
(2)令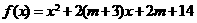 ,原命题等价于
,原命题等价于
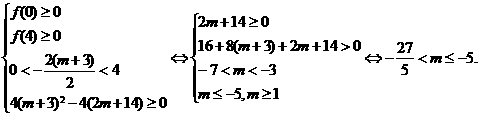
(3)令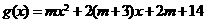 ,依题得
,依题得
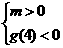 或
或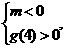 得
得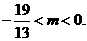
[评注]求解二次方程根的分布问题,结合二次函数图象,主要考虑三个方面的问题(1)判别式(2)对称轴(3)区间端点函数值
例4:已知二次函数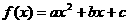 .
.
(1)若a>b>c, 且f(1)=0,证明f(x)的图象与x轴有2个交点;
(2)在(1)的条件下,是否存在m∈R,使得f(m)=- a成立时,f(m+3)为正数,若存在,证明你的结论,若不存在,说明理由;
(3)若对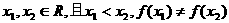 ,方程
,方程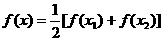 有2个不等实根,
有2个不等实根,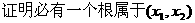
解: (1)
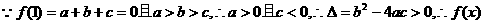
的图象与x轴有两个交点.
(2)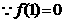 ,∴1是
,∴1是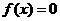 的一个根,由韦达定理知另一根为
的一个根,由韦达定理知另一根为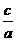 ,
,
∴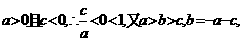
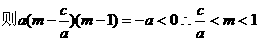
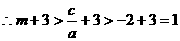
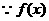 在(1,+∞)单调递增,
在(1,+∞)单调递增,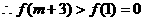 ,即存在这样的m使
,即存在这样的m使
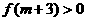
(3)令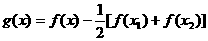 ,则
,则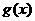 是二次函数.
是二次函数.
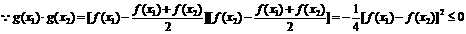
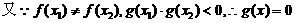 有两个不等实根,且方程
有两个不等实根,且方程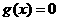 的根必有一个属于
的根必有一个属于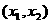 .
.
例5:(1)已知函数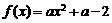 ,若
,若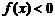 有解,求实数
有解,求实数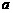 的取值范围;
的取值范围;
(2)已知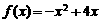 ,当
,当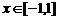 时,若
时,若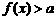 恒成立,求实数
恒成立,求实数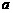 的取值范围。
的取值范围。
解:(1)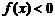 有解,即
有解,即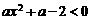 有解
有解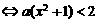 有解
有解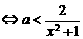 有解
有解
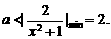 所以
所以
(2)当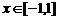 时,
时,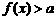 恒成立
恒成立
 又当
又当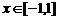 时,
时,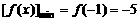 ,所以
,所以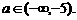
点评:“有解”与“恒成立”是很容易搞混的两个概念。一般地,对于“有解”与“恒成立”,有下列常用结论:(1)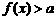 恒成立
恒成立
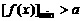 ;(2)
;(2)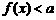 恒成立
恒成立
 ;(3)
;(3)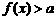 有解
有解
 ;(4)
;(4)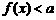 有解
有解

例6:(1)若函数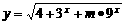 在区间
在区间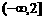 上有意义,求实数
上有意义,求实数 的取值范围;
的取值范围;
(2)若函数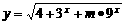 的定义域为
的定义域为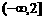 ,求实数
,求实数 的取值范围。
的取值范围。
解:(1)由题意知,当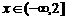 时,恒有
时,恒有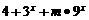
 ,即恒有
,即恒有
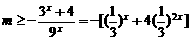 .
.
又因为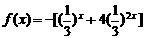 在
在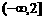 上单调递增,所以
上单调递增,所以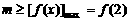
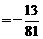 ,所以
,所以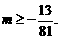
(2)由题意知,不等式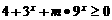 ,即
,即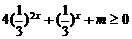 的解是
的解是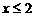 ,易解得,
,易解得,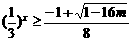 ,
,
则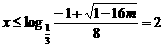 ,解方程
,解方程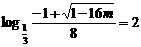 ,得
,得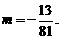
[点评]:“有意义”与“定义域”是两个不同的概念。一般地,在某个条件下函数“有意义”,是指在该条件下,使得函数有意义的某个式子总成立;而若某个条件为函数的“定义域”,则是指使得函数有意义的自变量的范围就是该条件。
4、.二次函数的图象与二次方程根的分布
由于二次函数图象与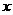 轴交点的横坐标即为二次方程的根,所以我们通常可借助二次函数
轴交点的横坐标即为二次方程的根,所以我们通常可借助二次函数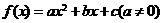 的图象来讨论二次方程
的图象来讨论二次方程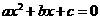 的实根分布情况。
的实根分布情况。
3、一元二次函数在区间的最值问题。
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com