
题目列表(包括答案和解析)
2.边长为1的等边三角形内,若有n2+1个点,则至少存在2点距离小于 .
.
1.边长为1的等边三角形内有5个点,那么这5个点中一定有距离小于0.5的两点.

2. 主要性质 在轴对称变换下,对应线段相等,对应直线(段)或者平行,或者交于对称轴,且这两条直线的夹角被对称轴平分。
例题:
[例1] P是平行四边形ABCD内一点,且∠PAB=∠PCB。
求证:∠PBA=∠PDA。
[例2]如图左:线段AA′,BB′,CC′交于点O,AA'=BB'=CC'=2,∠AOB'=∠BOC'=60°。
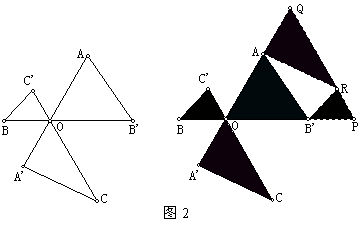 求证:S△AOB'+S△BOC'+S△COA'<
求证:S△AOB'+S△BOC'+S△COA'<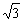
[例3] 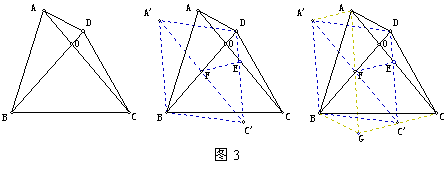 在两条对角线长度以及夹角一定的所有凸四边形中,试求周长最小的四边形。
在两条对角线长度以及夹角一定的所有凸四边形中,试求周长最小的四边形。
[例4] 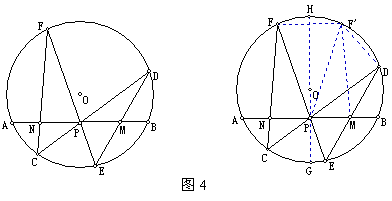 P是⊙O的弦AB的中点,过P点引⊙O的两弦CD、EF,连结DE交AB于M,连结CF交AB于N。求证:MP=NP。(蝴蝶定理)
P是⊙O的弦AB的中点,过P点引⊙O的两弦CD、EF,连结DE交AB于M,连结CF交AB于N。求证:MP=NP。(蝴蝶定理)
[例5]⊙O是给定锐角∠ACB内一个定圆,试在⊙O及射线CA、CB上各求一点P、Q、R,使得△PQR的周长为最小
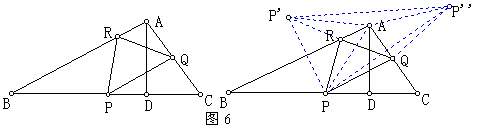 [例6]△ABC中,∠A≥90°,AD⊥BC于D,△PQR是它的任一内接三角形。求证:PQ+QR+RP>2AD。
[例6]△ABC中,∠A≥90°,AD⊥BC于D,△PQR是它的任一内接三角形。求证:PQ+QR+RP>2AD。
1.
定义 设l是一条给定的直线,S是平面上的一个变换,它把平面图形F上任一点X变到X',使得X与X'关于直线l对称,则S叫做以l为对称轴的轴对称变换。记为X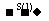 X',图形F
X',图形F F' 。
F' 。
2.主要性质 在平移变换下,对应线段平行且相等,直线变为直线,三角形变为三角形,圆变为圆。两对应点连线段与给定的有向线段平行(共线)且相等。
1.
定义 设 是一条给定的有向线段,T是平面上的一个变换,它把平面图形F上任一点X变到X',使得
是一条给定的有向线段,T是平面上的一个变换,它把平面图形F上任一点X变到X',使得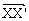 =
=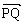 ,则T叫做沿有向线段
,则T叫做沿有向线段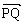 的平移变换。记为X
的平移变换。记为X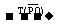 X',图形F
X',图形F F' 。
F' 。
例1. 任何实数x,y,
求证: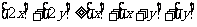
例2.
求:
例3.
设r是实数且满足条件:
求: (第9届美国数学邀请赛AIME试题)
(第9届美国数学邀请赛AIME试题)
例4.
在数列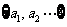 =
=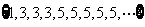 中每个奇数k出现k次,设有整数p,q,r存在,对所有正整数n,满足
中每个奇数k出现k次,设有整数p,q,r存在,对所有正整数n,满足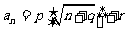 ,其中
,其中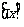 表示不大于x的最大整数,
表示不大于x的最大整数,
求: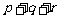 的值。(《数学通讯》问题征解题)
的值。(《数学通讯》问题征解题)
1)充分利用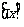 的定义,根据定义,任意实数
的定义,根据定义,任意实数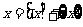 ,而0≤
,而0≤ <1,于是,将关于任意实数x的问题,归结到讨论区间(0,1)上的关于
<1,于是,将关于任意实数x的问题,归结到讨论区间(0,1)上的关于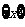 的问题。
的问题。
2)有意识的利用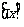 的性质,特别是前四个性质,因为这四个性质是直接由定义派生出来的,可以说是函数
的性质,特别是前四个性质,因为这四个性质是直接由定义派生出来的,可以说是函数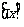 的本质属性的推论。
的本质属性的推论。
3)充分利用典型区间,设m=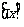 ,p=
,p=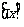 ,则x=m+p,其中0≤p<1,于是,问题归纳到在[0,1]上讨论。为此需要对区间(0,1)进行划分,分段讨论,又常分成几个相等的小段:
,则x=m+p,其中0≤p<1,于是,问题归纳到在[0,1]上讨论。为此需要对区间(0,1)进行划分,分段讨论,又常分成几个相等的小段: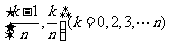 ,于是问题的讨论只要在典型区间
,于是问题的讨论只要在典型区间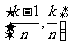 上进行即可。
上进行即可。
1)定义: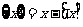 为x的小数部分,所以
为x的小数部分,所以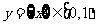
2)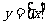 是不减函数,当
是不减函数,当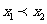 时,
时,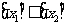
3)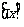 中整数部分可以外拿,
中整数部分可以外拿,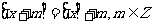
4) 有
有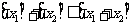
5)若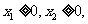 则
则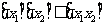

6)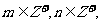 在
在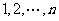 中,m的倍数有
中,m的倍数有 个
个
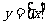 叫高斯函数,定义域为R,y是不超过x的最大整数。
叫高斯函数,定义域为R,y是不超过x的最大整数。
注:1)
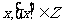
2)
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com