
题目列表(包括答案和解析)
4.已知函数 对于定义域内任何一个x都满足
对于定义域内任何一个x都满足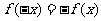 ,且
,且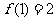 .(1)求
.(1)求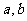 的值;(2)当
的值;(2)当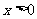 ,讨论函数
,讨论函数 单调性
单调性
3.对于函数 (x∈D)其中D为函数的定义域,若同时满足下列2个条件:
(x∈D)其中D为函数的定义域,若同时满足下列2个条件:
① 在定义域内是单调函数;
在定义域内是单调函数;
②存在区间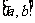
 D,使f(x)在
D,使f(x)在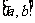 上的值域是
上的值域是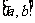 ,那么把
,那么把 (x∈D)称为闭函数。(1)求闭函数
(x∈D)称为闭函数。(1)求闭函数 符合条件②的区间
符合条件②的区间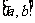 ;(2)判断函数
;(2)判断函数 ,x∈(0,+∞)是否为闭函数,说明理由
,x∈(0,+∞)是否为闭函数,说明理由
2.已知函数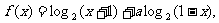 且
且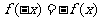
(1)求函数 的解析式;(2)求证:
的解析式;(2)求证: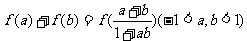
1.全集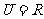 ,
,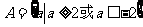 ,
,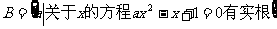 ,求
,求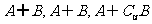
11.已知函数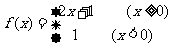 ,
,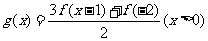
(1)求函数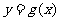 的解析式;
的解析式;
(2)求函数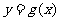 的最小值.
的最小值.
10.某宾馆有相同标准的床位100张,根据经验,当该宾馆的床价(即每张床价每天的租金)不超过10元时,床位可以全部租出,当床位高于10元时,每提高1元,将有3张床位空闲.
为了获得较好的效益,该宾馆要给床位订一个合适的价格,条件是:①要方便结账,床价应为1元的整数倍;②该宾馆每日的费用支出为575元,床位出租的收入必须高于支出,而且高出得越多越好.
若用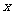 表示床价,用
表示床价,用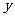 表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)
表示该宾馆一天出租床位的净收入(即除去每日的费用支出后的收入)
(1)把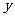 表示成
表示成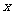 的函数,并求出其定义域;
的函数,并求出其定义域;
(2)试确定该宾馆床位定为多少时既符合上面的两个条件,又能使净收入最多?
解:(1)由已知有
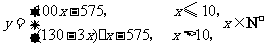
令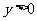 .
.
由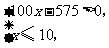 得
得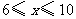 ,
,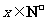
又由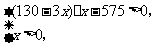 得
得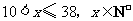
所以函数为
函数的定义域为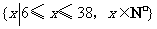 .
.
(2)当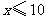 时,显然,当
时,显然,当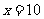 时,
时,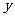 取得最大值为425(元);
取得最大值为425(元);
当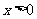 时,
时, ,
,
仅当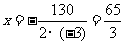 时,
时,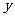 取最大值,
取最大值,
又 ,
,
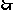 当
当 时,
时,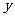 取得最大值,此时
取得最大值,此时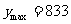 (元)
(元)
比较两种情况的最大值,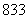 (元)
(元)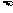 425(元)
425(元)
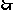 当床位定价为22元时净收入最多.
当床位定价为22元时净收入最多.
9、设函数 则实数
则实数 的取值范围是
.
的取值范围是
.
8、下列四个语句:(1) 有意义; (2)函数是其定义域到值域的对应;
有意义; (2)函数是其定义域到值域的对应;
(3)函数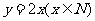 的图象是一直线;(4)函数
的图象是一直线;(4)函数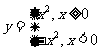 的图象是抛物线,
的图象是抛物线,
其中正确的个数是_______.
7、已知全集U={x|x2-3x+2≥0},A={x||x-2|>1},B=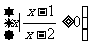 ,则(CUA)∩B=
,则(CUA)∩B=
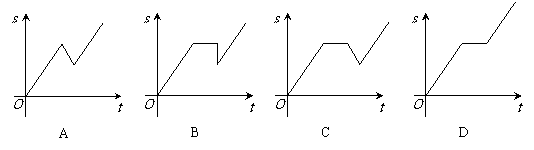
6.某同学家门前有一笔直公路直通长城,星期天,他骑自行车匀速前往旅游,他先前进了akm,觉得有点累,就休息了一段时间,想想路途遥远,有些泄气,就沿原路返回骑了bkm(b<a), 当他记起诗句“不到长城非好汉”,便调转车头继续前进. 则该同学离起点的距离s与时间t的函数关系的图象大致为( ).
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com