
题目列表(包括答案和解析)
7.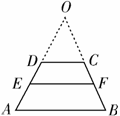 如图,在梯形
如图,在梯形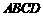 中,
中,
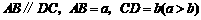 .若
.若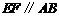 ,
,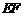 到
到 与
与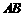 的距离之比为
的距离之比为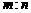 ,则可推算出:
,则可推算出: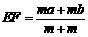 .试用
.试用
类 比的方法,推想出下述问题的结果.在上面的梯形
比的方法,推想出下述问题的结果.在上面的梯形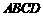 中,延长梯形两腰
中,延长梯形两腰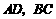 相交于
相交于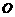 点,设
点,设 ,
,
的面积分别为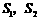 ,
,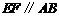 且
且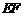 到
到 与
与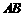 的距离之比为
的距离之比为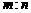 ,则
,则 的面积
的面积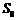 与
与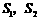 的关系是( )
的关系是( )
A.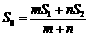 B.
B.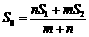
C.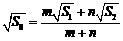 D.
D.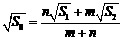
答案:C
6.观察式子: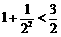 ,
,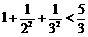 ,
,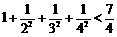 ,
, ,则可归纳出式子为( )
,则可归纳出式子为( )
A.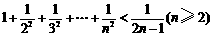
B.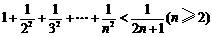
C.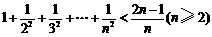
D.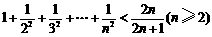
答案:C
5.(1)已知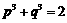 ,求证
,求证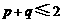 ,用反证法证明时,可假设
,用反证法证明时,可假设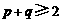 ,
,
(2)已知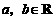 ,
,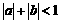 ,求证方程
,求证方程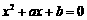 的两根的绝对值都小于1.用反证法证明时可假设方程有一根
的两根的绝对值都小于1.用反证法证明时可假设方程有一根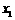 的绝对值大于或等于1,即假设
的绝对值大于或等于1,即假设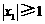 ,以下结论正确的是( )
,以下结论正确的是( )
A.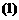 与
与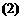 的假设都错误
的假设都错误
B.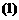 与
与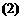 假设都正确
假设都正确
C.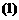 的假设正确;
的假设正确;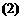 的假设错误
的假设错误
D.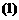 的假设错误;
的假设错误;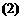 的假设正确
的假设正确
答案:D
4.在等差数列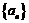 中,若
中,若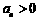 ,公差
,公差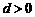 ,则有
,则有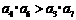 ,类经上述性质,在等比数列
,类经上述性质,在等比数列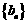 中,若
中,若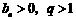 ,则
,则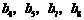 的一个不等关系是( )
的一个不等关系是( )
A.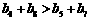 B.
B.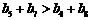
C.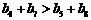
 D.
D.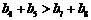
答案:B
3.在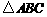 中,
中,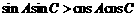 ,则
,则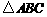 一定是( )
一定是( )
A.锐角三角形 B.直角三角形 C.钝角三角形 D.不确定
答案:C
2.结论为: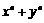 能被
能被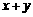 整除,令
整除,令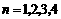 验证结论是否正确,得到此结论成立的条件可以为( )
验证结论是否正确,得到此结论成立的条件可以为( )
A.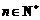 B.
B.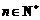 且
且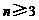
 C.
C.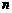 为正奇数 D.
为正奇数 D.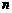 为正偶数
为正偶数
答案:C
1.分析法是从要证明的结论出发,逐步寻求使结论成立的( )
A.充分条件 B.必要条件 C.充要条件 D.等价条件
答案:A
19.已知f(x)是定义在(-1,1)的函数,并且满足下列条件:①对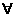 x1,x2∈(-1,1)都有f(x1)+f(x2)=
x1,x2∈(-1,1)都有f(x1)+f(x2)=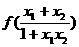 成立;②当x∈(-1,0)时,f(x)>0.请回答下列问题:
成立;②当x∈(-1,0)时,f(x)>0.请回答下列问题:
(1)判断f(x)在(-1,1)上的奇偶性,并说明理由;
(2)判断f(x)在(0,1)上的单调性,并说明理由.
答案:(1)∵对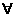 x1,x2∈(-1,1)时,f(x1)+f(x2)=
x1,x2∈(-1,1)时,f(x1)+f(x2)=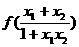 都成立, ∴令x1=x2=0,得f(0)=0,∴对于
都成立, ∴令x1=x2=0,得f(0)=0,∴对于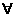 x∈(-1,1),f(x)+f(-x)=
x∈(-1,1),f(x)+f(-x)=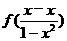 =0,所以对于
=0,所以对于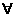 x∈(-1,1),有f(-x)=-f(x),所以f(x)在(-1,1)上是奇函数
x∈(-1,1),有f(-x)=-f(x),所以f(x)在(-1,1)上是奇函数
(2)设0<x1<x2<1,f(x1)-f(x2)=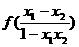 ,因0<x1<x2<1,∴x1-x2<0,1-x1x2>0,∴-1<
,因0<x1<x2<1,∴x1-x2<0,1-x1x2>0,∴-1<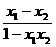 <0,则f(x1)>f(x2),∴f(x)在(0,1)上是减函数
<0,则f(x1)>f(x2),∴f(x)在(0,1)上是减函数
18.已知定义在R上的奇函数f(x),当x∈(-1,0)时,f(x)=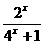 .
.
(1)求f(x)在(-1,1)上的表达式;
(2)证明f(x)在(-1,0)上是增函数.
答案:1(1)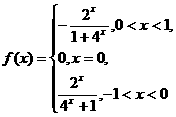
(2)设-1<x1<x2<0,则f(x1)-f(x2)= ,∵ x1<x2<0,∴
,∵ x1<x2<0,∴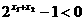 ,
,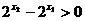 ,∴f(x1)-f(x2)<0,即f(x1)<f(x2),所以,f(x)在(-1,0)上是增函数
,∴f(x1)-f(x2)<0,即f(x1)<f(x2),所以,f(x)在(-1,0)上是增函数
17.已知函数f(x)=loga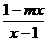 (a>0,a≠1)是奇函数.
(a>0,a≠1)是奇函数.
(1)求m的值;
(2)判断f(x)在区间(1,+∞)上的单调性.
答案:(1)∵f(x)为奇函数, ∴loga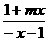 =-loga
=-loga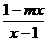 (对
(对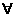 x∈R恒成立)
x∈R恒成立)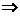 m=-1
m=-1
(2)∵f(x)=loga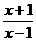 (x<-1或x>1),∴f(x)=loga(1+
(x<-1或x>1),∴f(x)=loga(1+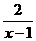 ),∴(i)当0<a<1时,f(x)在(1,+∞)上是增函数;(ii)当a>1时,f(x)在(1,+∞)上是减函数
),∴(i)当0<a<1时,f(x)在(1,+∞)上是增函数;(ii)当a>1时,f(x)在(1,+∞)上是减函数
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com