
题目列表(包括答案和解析)
12.设A={x||2x-1|>1},B={x||2x-a|≤1},A∩B=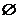 ,A∪B=R,求实数a的值.
,A∪B=R,求实数a的值.
解:|2x-1|>1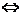 2x-1>1或2x-1<-1,即x>1或x<0,即A={x|x>1或x<0};解|2x-a|≤1,得-1≤2x-a≤1,即
2x-1>1或2x-1<-1,即x>1或x<0,即A={x|x>1或x<0};解|2x-a|≤1,得-1≤2x-a≤1,即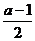 ≤x≤
≤x≤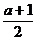 ,即B={x|
,即B={x|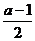 ≤x≤
≤x≤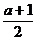 }.由A∩B=
}.由A∩B=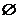 ,A∪B=R,图示如下:
,A∪B=R,图示如下:
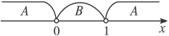
可得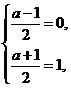 解得a=1.
解得a=1.
11.不等式|x-2|+|x-3|<9的解集是________________.
答案:{x|-2<x<7}
解析:当x≥3时,原不等式为x-2+x-3<9,解得x<7,即有3≤x<7;当2≤x<3时,为x-2+3-x<9,即1<9成立,即有2≤x<3;当x<2时,为2-x+3-x<9,解得x>-2,即有-2<x<2.
综合得原不等式的解集为{x|3≤x<7}∪{x|2≤x<3}∪{x|-2<x<2}={x|-2<x<7}.
10.不等式|6-|2x+1||>1的解集是________________.
答案:{x|x<-4或-3<x<2或x>3}
解析:原不等式等价于6-|2x+1|>1或6-|2x+1|<-1,又等价于-5<2x+1<5或2x+1>7或2x+1<-7.解之可得.
9.若|x-4|+|x-3|<a在R上的解集为空集,则常数a的取值范围是( )
A.a<3 B.a≤1 C.a>3 D.a>3或a<-4
答案:B
解析:由几何意义:|x-4|+|x-3|的最小值为1,则当a≤1时,原不等式的解集为空集.
8.已知集合M={x|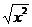 ≤1},P={x|x-t>0},要使M∩P=
≤1},P={x|x-t>0},要使M∩P=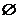 ,则t的取值范围是( )
,则t的取值范围是( )
A.{t|t≥1} B.{t|t<1} C.{t|t>1} D.{t|t≤1}
答案:A
解析:M={x|-1≤x≤1},P={x|x>t},由M∩P=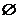 知t≥1.
知t≥1.
7.已知集合A={x||x+7|>10},B={x|?|x-5|?<2c},又A∩B=B,求实数c的范围.
解:先解|x+7|>10,得x+7>10或x+7<-10,有x>3或x<-17,即A={x|x>3若x<-17}.
由A∩B=B得B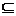 A,对B讨论如下情况:
A,对B讨论如下情况:
(1)B=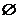 有c≤0;
有c≤0;
(2)B≠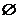 有c>0,解|x-5|<2c,得-2c<x-5<2c,有5-2c<x<5+2c.要使B
有c>0,解|x-5|<2c,得-2c<x-5<2c,有5-2c<x<5+2c.要使B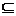 A,必须有5+2c≤-17或5-2c≥3,如图所示:
A,必须有5+2c≤-17或5-2c≥3,如图所示:

解得c≤-11或c≤1.
取c≤1,即0<c≤1.
由(1)(2)知实数c的取值范围是
{c|c≤0}∪{c|0<c≤1=={c|c≤1}.
能力提升 踮起脚,抓得住!
6.|x-1|>|x+1|的解集是______________.
答案:{x|x<0}
解析:原不等式可化为(x-1)2>(x+1)2,解得x<0.
5.对于任意实数x,不等式|x|≥m-1恒成立,则实数m的取值范围是_________________.
答案:m≤1
解析:|x|≥m-1对一切实数x恒成立,则m-1应不大于|x|的最小值,即m-1≤0,得m≤1.
4.在数轴上与原点距离不大于2的点的坐标的集合是( )
A.{x|-2<x<2} B.{x|0<x≤2}
C.{x|-2≤x≤2} D.{x|x≥2或x≤-2}
答案:C
解析:由绝对值的几何意义易知.
3.已知a>1,则不等式|x|+a>1的解集是( )
A.{x|a-1<x<1-a} B.{x|x<a-1或x>1-a}
C. D.R
D.R
答案:D
解析:由|x|+a>1,得|x|>1-a.
∵a>1,∴1-a<0.故该不等式的解集为R.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com