
题目列表(包括答案和解析)
16.解关于x的不等式(x-2)(ax-2)>0.
解:不等式的解及其结构与a相关,所以必须分类讨论.
当a=0时,原不等式化为
x-2<0,其解集为{x|x<2};
当a<0时,由于2>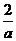 ,原不等式化为
,原不等式化为
(x-2)(x-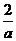 )<0,其解集为{x|
)<0,其解集为{x|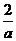 <x<2};
<x<2};
当0<a<1时,因2<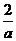 ,原不等式化为(x-2)(x-
,原不等式化为(x-2)(x-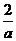 )>0,其解集为{x|x<2或x>
)>0,其解集为{x|x<2或x>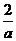 };
};
当a=1时,原不等式化为(x-2)2>0,其解集为{x|x≠2};
当a>1时,由于2>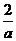 ,原不等式化为(x-2)(x-
,原不等式化为(x-2)(x-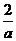 )>0,其解集为{x|x<
)>0,其解集为{x|x<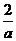 或x>2}.
或x>2}.
从而可以写出不等式的解集为
a=0时,{x|x<2};
a<0时,{x|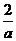 <x<2};
<x<2};
0<a<1时,{x|x<2或x>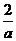 };
};
a=1时,{x|x≠2};
a>1时,{x|x<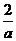 或x>2}.
或x>2}.
15.不等式x2-3|x|+2>0的解集为_________________.
答案:{x|x<-2或-1<x<1或x>2}
解析:原不等式即为|x|2-3|x|+2>0,
即(|x|-2)(|x|-1)>0,
解得|x|>2或|x|<1.
由|x|>2得x>2或x<-2;
由|x|<1得-1<x<1.
综上,原不等式的解集为{x|x<-2或-1<x<1或x>2}.
14.若方程ax2+bx+c=0的两实根为x1、x2,集合S={x|x>x1},T={x|x>x2},P={x|x<x1},Q={x|x<x2},则不等式ax2+bx+c>0(a>0)的解集为( )
A.(S∩T)∪(P∩Q) B.(S∩T)∩(P∩Q)
C.(S∪T)∪(P∪Q) D.(S∪T)∩(P∪Q)
答案:A
解析:该方程的解集为x大于大根或x小于小根,“S∩T”相当于“x大于大根”,“P∩Q”相当于“x小于小根”,“(S∩T)∪(P∩Q)”相当于“x大于大根或x小于小根”.
13.已知集合A={x|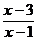 ≤0},B={x|x2-3x-c≤0}.
≤0},B={x|x2-3x-c≤0}.
(1)若A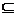 B,求c;
B,求c;
(2)若B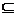 A,求c.
A,求c.
解:A={x|1<x≤3=,B={x|x2-3x-c≤0},
(1)由A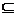 B,可知函数y=x2-3x-c在{x|1<x≤3}上恒有y≤0,
B,可知函数y=x2-3x-c在{x|1<x≤3}上恒有y≤0,
即x2-3x-c≤0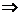 c≥x2-3x=(x-
c≥x2-3x=(x-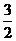 )2-
)2-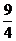 ,
,
故ymax=0,即c≥0.
(2)由B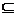 A可知,B可能为
A可知,B可能为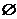 ,可能非空.
,可能非空.
①B=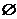 时,Δ=9+4c<0
时,Δ=9+4c<0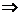 c<-
c<-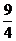 ;
;
②B≠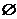 时,此时方程x2-3x-c=0的两根为x1、x2,即如图所示.
时,此时方程x2-3x-c=0的两根为x1、x2,即如图所示.
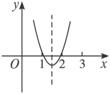
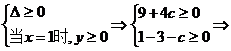 -
-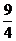 ≤c≤-2.
≤c≤-2.
综合①②知c≤-2即为所求.
拓展应用 跳一跳,够得着!
12.若关于x的不等式(m2+4m-5)x2-4(m-1)x+?3>0?对一切实数x恒成立,求m的取值范围.
解:m2+4m-5=0得m=-5或m=1.
(1)当m=1时原不等式变为3>0对x∈R恒成立,故m=1;
(2)当m=-5时原不等式变为24x+3>0,解集为{x|x>-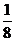 }≠R,不合题意,即m≠-5;
}≠R,不合题意,即m≠-5;
(3)当m≠1且m≠-5时,m2+4m-5≠0,一元二次不等式(m2+4m-5)x2-4(m-1)x+3>0解集为R
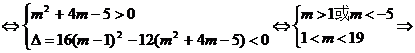 1<m<19.
1<m<19.
∴总之,1≤m<19.
11.已知集合A={x∈R|x2-x-2≤0},B={x∈R|a<x<a+3}且A∩B=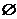 ,则实数a的取值范围是___________________.
,则实数a的取值范围是___________________.
答案:a≥2或a≤-4
解析:A={x|-1≤x≤2}.
∵A∩B=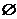 ,∴a≥2或a+3≤-1,
,∴a≥2或a+3≤-1,
即a≥2或a≤-4.
10.已知不等式ax2+bx+2>0的解集是{x|-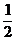 <x<
<x<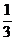 },则a-b=_________________.
},则a-b=_________________.
答案:-10
解析:由题中条件知a<0且-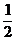 与
与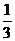 是方程ax2+bx+2=0的两个根,代入方程,得
是方程ax2+bx+2=0的两个根,代入方程,得
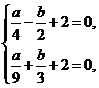
解之,得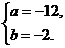 ∴a-b=-10.
∴a-b=-10.
另外,本题也可利用韦达定理来解.
由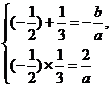 也可得结果.
也可得结果.
9.关于x的不等式x2-ax-6a<0的解集为{x|α<x<β}?(β-α≤5),则a的取值范围为( )
A.{a|-25≤a≤1} B.{a|a≤-25或a≥1}
C.{a|-25≤a≤0或1≤a≤24} D.{a|-25≤a<-24或0<a≤1}
答案:D
解析:可知x2-ax-6a=0有两根,即Δ=a2+24a>0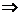 a>0或a<-24①,又有β-α=
a>0或a<-24①,又有β-α=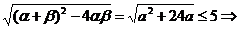 a2+24a-25≤0
a2+24a-25≤0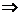 -25≤a≤1②.
-25≤a≤1②.
由①②知0<a≤1或-25≤a<-24.
8.当a<0时,不等式42x2+ax-a2<0的解集为( )
A.{x|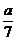 <x<-
<x<-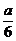 }
B.{x|-
}
B.{x|-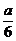 <x<
<x<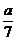 }
}
C.{x|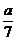 <x<-
<x<-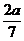 }
D.空集
}
D.空集
答案:A
解析:42x2+ax-a2<0,
∴(6x+a)(7x-a)<0,a<0.
∴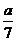 <x<-
<x<-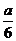 .
.
7.设关于x的不等式(a-2)x2+2(a-2)x-4<0的解集为R.求a的取值范围.
解:(1)当a-2=0,即a=2时,
原不等式可化简为-4<0,成立.
∴a=2可取.∴x∈R.
(2)当a-2≠0,即a≠2时,
若保证x∈R,则有
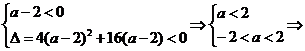 -2<a<2.
-2<a<2.
综上,-2<a≤2.
能力提升 踮起脚,抓得住!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com