
题目列表(包括答案和解析)
4.用反证法证明“如果a>b>0,那么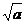 >
>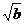 ”假设的内容应是( )
”假设的内容应是( )
A.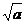 =
=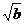 B.
B.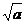 <
<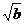
C.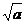 ≤
≤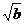 D.
D.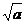 <
<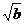 且
且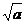 =
=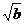
答案:C
解析:“>”的反面为“≤”.
3.命题:“若a、b都是偶数,则a+b是偶数”的逆否命题是( )
A.若a+b是偶数,则a、b都不是偶数
B.若a+b是偶数,则a、b不都是偶数
C.若a+b不是偶数,则a、b都不是偶数
D.若a+b不是偶数,则a、b不都是偶数
答案:D
解析:注意“都是”的否定为“不都是”.
2.关于命题“平行四边形的两组对边分别相等”,下列论述中,正确的是( )
A.逆命题是假命题 B.否命题是假命题
C.逆否命题是真命题 D.以上答案都不对
答案:C
解析:原命题为真命题,所以逆否命题为真命题.
1.命题“若A∩B=A,则A∪B=B”的否命题是( )
A.若A∪B=B,则A∩B=A B.若A∩B≠A,则A∪B≠B
C.若A∪B≠B,则A∩B≠A D.若A∪B≠B,则A∩B=A
答案:B
解析:条件与结论要同时否定.
16.二次函数f(x)=ax2+bx+c(a≠0),且Δ=b2-4ac,试判断下列命题的真假,若命题为假,则举出一个反例说明;若命题为真,则证明之.
命题(1):若Δ<0,则af(x)≤0;
命题(2):若Δ>0,x1、x2是方程f(x)=0的两根,且x1<x2,则当x1<x<x2时,af(x)<0;当x<x1或x>x2时,af(x)>0.
解:(1)假命题.若a>0,则af(x)>0,如f(x)=x2+1.
(2)真命题.a>0时,f(x)=a(x-x1)(x-x2).
当x1<x<x2时,f(x)<0,af(x)<0;
当x<x1或x>x2时,f(x)>0,af(x)>0,a<0时,f(x)=a(x-x1)(x-x2).
当x1<x<x2时,f(x)>0,af(x)<0;
当x<x1或x>x2时,f(x)<0,af(x)>0.
15.要使x∈A∩B成立,必须x∈A且x∈B;而要使x∈A∪B成立,只需_________________.(给出一个条件即可)
答案:x∈A但x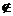 B(或x
B(或x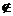 A但x∈B,或x∈A且x∈B,任填一种)
A但x∈B,或x∈A且x∈B,任填一种)
解析:“x∈A∪B”,即为“x∈A或x∈B”,它具有三层意思:①x∈A但x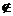 B;②x
B;②x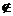 A但x∈B;③x∈A且x∈B,这三种中的任一种成立,就可以说x∈A∪B成立.
A但x∈B;③x∈A且x∈B,这三种中的任一种成立,就可以说x∈A∪B成立.
14.四个孩子在教室旁边玩球,突然传来一阵打碎玻璃的响声,王老师跑去察看,发现一扇窗户被打破了,老师说:“一定是你们中一个打破的.”小宝说:“是小丹打破的.”小丹说:“是小爽打破的.”小爽说:“小丹说谎.”贝贝说:“我没有打破窗子.”如果只有一个小孩说的是实话,那么真实情况是( )
A.小宝说的是实话,是小丹打破的 B.小丹说的是实话,是小爽打破的
C.贝贝说的是实话,是小宝打破的 D.小爽说的是实话,是贝贝打破的
答案:D
解析:因“非p”和“p”之中必有一真,则小丹和小爽之中必有一人说的是实话,若小丹说的是
实话,是小爽打破的,这与贝贝说的假话相矛盾;若小爽说的是实话,是贝贝打破的,此时,与小宝、小丹、贝贝都说假话相吻合,故选D.
13.有位同学认为:“命题p与非p可以同时为假命题.”他举例如下:
设p:若三角形有两个内角相等,则此三角形是锐角三角形.
非p:若三角形有两个内角相等,则此三角形不是锐角三角形.
显然p与非p都是假命题,故其结论正确.
请问:该同学的观点是否正确?若正确,请说明成立的条件,并适当推广;若不正确,请指出错在哪里,错误的原因是什么,并给出正确结论,简要总结一下经验教训.
解:该同学的观点不正确.非p中的判断词“不是”错误.因为p中的判断词“是”在此处为“必定是”“都是”的含义,故它的否定词不应为“不是”,而应为“不一定是”“不都是”,即“非p”错.
p的非p形式ξ?
非p:若三角形有两内角相等,则此三角形不一定是锐角三角形.
显然,非p为正确命题.
通过对此题的解剖,告诫我们要学会正确否定,要正确理解和掌握一些常见的判断词及其否定词.
拓展应用 跳一跳,够得着!
12.已知命题p:|x2-x|≥6,q:x∈Z,且“p且q”与“非q”同时为假命题,求x的值.
解:∵p且q为假,
∴p、q至少有一命题为假.又“非q”为假,
∴q为真,从而可知p为假.
由p为假且q为真,可得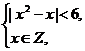
即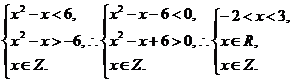
∴x的值为-1,0,1,2.
11.下面命题:
(1)5>4或4>5;(2)9≥3;(3)菱形的两条对角线互相垂直;(4)对角线垂直的四边形是菱形;(5)正方形既是矩形,也是菱形;?(6)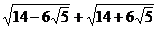 不是有理数.
不是有理数.
其中,是真命题的序号是________________.
答案:(1)(2)(3)(5)
解析:对于(4),对角线互相垂直且平分的四边形才是菱形;
对于(6),可化为|3-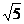 |+|3+
|+|3+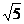 |=6.
|=6.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com