
题目列表(包括答案和解析)
6.若函数y=f(x)的定义域是[-1,1],则函数y=f(x+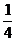 )+f(x-
)+f(x-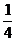 )的定义域是_________________.
)的定义域是_________________.
答案:[-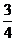 ,
,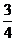 ]
]
解析: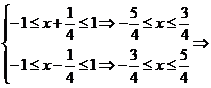 -
-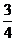 ≤x≤
≤x≤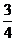 .
.
5.已知函数y= 的定义域为R,则实数m的取值范围是______________.
的定义域为R,则实数m的取值范围是______________.
答案:0≤m≤1
解析:依题意mx2-6mx+m+8≥0,对于x∈R恒成立,则m=0或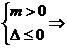 0<m≤1,故m的取值范围是0≤m≤1.
0<m≤1,故m的取值范围是0≤m≤1.
4.函数y=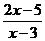 的值域是{y|y≤0或y≥4},则f(x)的定义域为( )
的值域是{y|y≤0或y≥4},则f(x)的定义域为( )
A.(-∞,3)∪(3,+∞)
B.[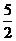 ,3])∪(3,
,3])∪(3,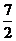 ]
]
C.(-∞,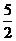 )∪[
)∪[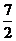 ,+∞]
D.[
,+∞]
D.[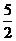 ,
,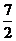 ]
]
答案:B
解析:由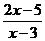 ≥4或
≥4或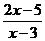 ≤0易得.
≤0易得.
3.下列函数中值域为(0,+∞)的是( )
A.y=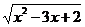 B.y=3x+1(x>0)
B.y=3x+1(x>0)
C.y=x2+x+2
D.y=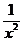
答案:D
解析:分别求出各函数的值域再比较.
2.若函数f(x)的定义域是[0,1],则f(x+a)·f(x-a)(0<a<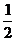 )的定义域是( )
)的定义域是( )
A.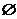 B.[a,1-a]
B.[a,1-a]
C.[-a,1+a] D.[0,1]
答案:B
解析:由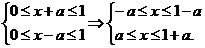 借助数轴易得:当0<a<
借助数轴易得:当0<a<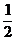 时,-a<a<1-a<1+a,故函数y=f(x+a)·f(x-a)的定义域为[a,1-a].
时,-a<a<1-a<1+a,故函数y=f(x+a)·f(x-a)的定义域为[a,1-a].
1.函数y=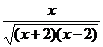 的定义域是( )
的定义域是( )
A.{x|-2<x<2} B.{x|x>2}
C.{x|-2<x<0或0<x<2} D.{x|x>2或x<-2}
答案:D
解析:定义域是使解析式有意义的x的取值范围,则(x+2)(x-2)>0.
16.如图所示,等腰梯形的两底分别为AD=2a,BC=a,∠BAD=45°,直线MN⊥AD,交AD于M,交折线ABCD于N,设AM=x,试将梯形ABCD位于直线MN左侧的面积y表示成x的函数,并求此函数的定义域.
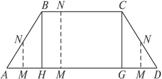
解:过B、C分别作边AD的垂线,垂足分别为H和G,则AH=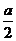 ,AG=
,AG=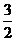 a,当M位于H左侧
a,当M位于H左侧
时,AM=x,MN=x.故y=S△AMN=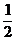 x2(0≤x<
x2(0≤x<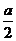 );
);
当M位于H、G之间时,y=S梯形ABNM=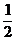 (AM+BN)·MN=
(AM+BN)·MN=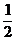 (x+x-
(x+x-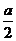 )·
)·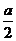 =
=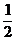 ax-
ax-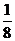 a2(
a2(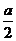 ≤x<
≤x<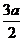 );
);
当M位于G、D之间时,y=S梯形ABCD-S△DMN=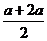 ·
·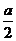 ·-
·-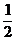 (2a-x)2=-
(2a-x)2=-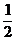 x2+2ax-
x2+2ax-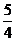 a2(
a2(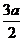 ≤x≤2a).
≤x≤2a).
故y=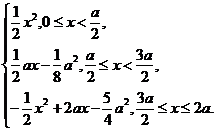
其定义域为[0,2a],值域为[0,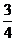 a2].
a2].
15.设A={a,b,c},B={-1,0,1},映射f:A→B满足f(a)=f(b)+f(c),则映射f:A→B的个数有_______个.
答案:7
解析:(1)当A中元素都对应0时,满足f(a)=f(b)+f(c),有一种映射.
(2)当A中元素对应B中的两个元素时,满足f(a)=f(b)+f(c),有四种映射:1=1+0,1=0+1,
-1=-1+0,-1=0+(-1).
(3)当A中元素对应B中三个元素时,满足f(a)=f(b)+f(c),有两种映射:0=1+(-1),0=(-1)+1.
∴满足条件的映射共有7个.
14.已知定义域为R的函数f(x)满足f(a+b)=f(a)·f(b)(a、b∈R)且f(x)>0,若f(1)= 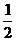 ,则f(-2)等于( )
,则f(-2)等于( )
A.2
B.4
C.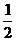 D.
D.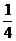
答案:B
解析:由f(a+b)=f(a)·f(b),知f(0+0)=f2(0)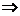 f(0)=1(f(x)>0),
f(0)=1(f(x)>0),
又f(2)=f(1+1)=f2(1)=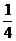 ,
,
f(2-2)=f(2)·f(-2)=f(0)=1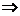 f(-2)=
f(-2)=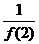 =4.
=4.
13.已知函数f(x)、g(x)同时满足条件:对一切实数x、y都有g(x-y)=g(x)·g(y)+f(x)·f(y);f(-1) =-1,f(0)=0,f(1)=1.试求g(0),g(1),g(2)的值.
解:由g(x-y)=g(x)·g(y)+f(x)·f(y)知,
g(x)=g(x-0)=g(x)·g(0)+f(x)·f(0),又f(0)=0,
故g(x)=g(x)·g(0) g(0)=1(g(x)不恒为零,否则g(0)=g(1-1)=g2(1)+f2(1)=0
g(0)=1(g(x)不恒为零,否则g(0)=g(1-1)=g2(1)+f2(1)=0 f(1)=0与f(1)=1矛盾).
f(1)=0与f(1)=1矛盾).
又g(-x)=g(0-x)=g(0)·g(x)+f(0)·f(x)=g(x) g(-1)=g(1),
g(-1)=g(1),
又g(0)=g(1-1)=g2(1)+f2(1)=1 g(1)=0(f(1)=1),则g(-1)=g(1)=0.
g(1)=0(f(1)=1),则g(-1)=g(1)=0.
g(2)=g[1-(-1)]=g(1)·g(-1)+f(1)·f(-1)=-1.
拓展应用 跳一跳,够得着!
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com