2.北京市为成功举办2008年奥运会,决定从2003年到2007年五年间更新市内现有的全部出租车.若每年更新的车辆数比前一年递增10%,则2003年底更新现有总车辆数的(参考数据为

1.某种细胞分裂时,由1个分裂成2个,2个分裂成4个,…,一个这样的细胞分裂x次后,得到的细胞个数y与x的函数关系式为(　　 )

A.y=2^x B.y=2x(x∈N^*)

C.y=2^x(x∈N^*)　　　　　　　　　　　　 D.y=log₂x

答案：C

解析：应注意函数的定义域.

16.已知函数f(x)对任意x、y∈R,总有f(x)+f(y)=f(x+y),且当x>0时,f(x)<0,f(1)=-.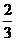

(1)求证:f(x)是R上的减函数;

(2)求f(x)在［-3,3］上的最大值和最小值.

(1)证明:令x=y=0,f(0)=0,令y=-x可得f(-x)=-f(x).

在R上任取x₁>x₂,则f(x₁)-f(x₂)=f(x₁)+f(-x₂)=f(x₁-x₂).

∵x₁>x₂,

∴x₁-x₂>0.

又∵x>0时f(x)<0,

∴f(x₁-x₂)<0,

即f(x₁)-f(x₂)>0.

由定义可知f(x)在R上为单调递减函数.

(2)解：∵f(x)在R上是减函数,

∴f(x)在［-3,3］上也是减函数.

∴f(-3)最大,f(3)最小.

f(3)=f(2)+f(1)=f(1)+f(1)+f(1)=3×(-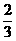)=-2.

∴f(-3)=-f(3)=2,

即f(x)在［-3,3］上最大值为2,最小值为-2.

15.函数y=f(x)是定义在R上的减函数,则y=f(|x+2|)的单调减区间是____________________.

答案：［-2,+∞)

解析：∵y=f(u)在R上递减,

u=|x+2|在［-2,+∞)上递增,在(-∞,-2]上递减,

∴y=f(|x+2|)在［-2,+∞)上递减.

14.(四川成都模拟)已知f(x)是R上的增函数,若令F(x)=f(1-x)-f(1+x),则F(x)是R上的(　　 )

A.增函数　　　　　　　　　　　　　　　　　　　 B.减函数

C.先减后增的函数　　　　　　　　　　　　　　　 D.先增后减的函数

答案：B

解析：取f(x)=x,则F(x)=(1-x)-(1+x)=-2x为减函数.

13.设函数y=f(x)(x∈R且x≠0)对任意非零实数x、y都有f(xy)=f(x)+f(y)成立.

(1)求证:f(1)=f(-1)=0且f(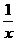)=-f(x)(x≠0);

(2)判断f(x)与f(-x)的关系;

(3)若f(x)在(0,+∞)上单调递增,解不等式f(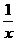)-f(2x-1)≥0.

(1)证明:令x=y=1,则f(1)=f(1)+f(1)?得f(1)=0.

再令x=y=-1,则f(1)=f(-1)+f(-1)得f(-1)=0.

对任意x≠0,有f(x)+f(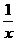)=f(1)=0,

∴f(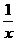)=-f(x).

(2)解：对任意x∈R且x≠0,有f(-x)+f(-1)=f(x),

∴f(-x)=f(x).

(3)解：∵f(x)在(0,+∞)上单调递增,则f(x)在(-∞,0)上单调递减,则f(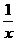)=-f(x),则-f(x)-f(2x-1)≥0f(x)+f(2x-1)≤0,即f［x(2x-1)］≤00<|x(2x-1)|≤1,解得-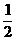≤x≤1且x≠0,x≠.

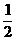拓展应用　 跳一跳,够得着!

12.已知函数f(x)的定义域为(-1,1),求满足下列条件的实数a的取值范围:

(1)f(x)在定义域内单调递减;

(2)f(1-a)<f(a²-1).

解：∵f(1-a)<f(a²-1),

又f(x)在定义域(-1,1)内单调递减,则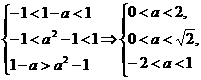

或-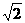<a<00<a<1.

故a的取值范围为{a|0<a<1}.

11.函数y=-x²-10x+11在区间［-1,2］上的最小值是________________.

答案：-13

解析：因为y=-x²-10x+11=-(x+5)²+36,根据二次函数的性质可知函数在［-1,2］上是减函数,故函数的最小值是f(2)=-2²-10×2+11=-13.

10.y=f(x)在［0,+∞］上为减函数,则f(π)、f(3)、f(4)?的大小关系为_______________.

答案：f(3)>f(π)>f(4)

解析：0<3<π<4<+∞,

且函数f(x)的减区间为［0,+∞］,∴f(3)>f(π)>f(4).

9.已知函数f(x)在定义域［a,b］上是单调函数,函数值域为［-3,5］,则以下说法正确的是(　　 )

A.若f(a)f(b)<0,则存在x₁∈［a,b］,使f(x₁)=0

B.f(x)在区间［a,b］上有最大值f(b)=5

C.f(x)在区间［a,b］上有最小值f(a)=-3

D.f(x)在区间［a,b］上有最大值不是f(b),最小值也不是f(a)

答案：A

解析：若函数单调递增,则排除D,若函数单调递减,则排除B、C,由此知选A.