
题目列表(包括答案和解析)
5.已知函数f(x)存在反函数,若点(a,b)在f(x)的图象上,则下列各点中必在其反函数图象上的点是( )
A.(f-1(b),b) B.(a,f-1(a))
C.(f(a),f-1(b)) D.(f-1(b),f(a))
答案:C
解析:由(a,b)在y=f(x)图象上,则(b,a)在y=f-1(x)图象上,且b=f(a),则a=f-1(b).
4.(四川成都模拟)已知f(x)=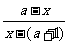 ,且f-1(x-1)的图象的对称中心是(0,3),则a的值为( )
,且f-1(x-1)的图象的对称中心是(0,3),则a的值为( )
A.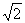 B.2
C.
B.2
C.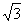 D.3
D.3
答案:B
解析:f-1(x)=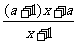 ,f-1(x-1)=
,f-1(x-1)=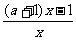 ,其对称中心是(0,a+1),∴a+1=3
,其对称中心是(0,a+1),∴a+1=3 a=2.
a=2.
3.如图,设函数y=1-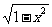 (-1≤x≤0),则函数y=f-1(x)的图象是图中的( )
(-1≤x≤0),则函数y=f-1(x)的图象是图中的( )

答案:B
解析:易知点(-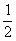 ,1-
,1-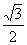 )在原函数图象上,故(1-
)在原函数图象上,故(1-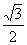 ,-
,-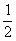 )在其反函数图象上,首先排除A、C,又1-
)在其反函数图象上,首先排除A、C,又1-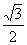 <
<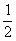 ,故点(1-
,故点(1-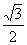 ,-
,-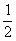 )在直线x=
)在直线x=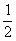 左边,排除D,选B.
左边,排除D,选B.
2.已知f(x)=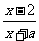 的图象关于直线y=x对称,则a的取值是( )
的图象关于直线y=x对称,则a的取值是( )
A.-1 B.1 C.-2 D.0
答案:A
解析:由y=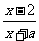 ,得x=
,得x=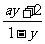 ,故f-1(x)=
,故f-1(x)=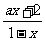 ,因函数f(x)的图象关于直线y=x对称,则f(x)与其反函数f-1(x)为同一函数,易得a=-1.
,因函数f(x)的图象关于直线y=x对称,则f(x)与其反函数f-1(x)为同一函数,易得a=-1.
1.点(3,5)在函数y=ax+b的图象上,又在其反函数的图象上,则a、b的值分别为( )
A.a=-1,b=7 B.a=-1,b=-8 C.a=-1,b=8 D.以上都不对
答案:C
解析:由已知得点(3,5)和点(5,3)在直线y=ax+b上,
∴
16.(1)已知f(x)=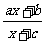 (a、b、c是常数)的反函数是f-1(x)=
(a、b、c是常数)的反函数是f-1(x)=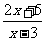 ,求a+b+c的值.
,求a+b+c的值.
(2)设点P(-1,-2)既在函数f(x)=ax2+b(x≤0)的图象上,又在f(x)的反函数的图象上,求f-1(x).
解:(1)设y=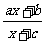 ,解得x=
,解得x=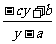 ,
,
即f-1(x)=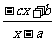 ,
,
因此,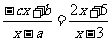 ,
,
由对应项系数相等得a=3,b=5,c=-2,
∴a+b+c=6.
(2)点P(-1,-2)在f(x)=ax2+b上,则-2=a(-1)2+b, ①
又∵点P(-1,-2)在f-1(x)上,
∴点(-2,-1)在f(x)上.
∴-1=a(-2)2+b. ②
由①②联立,解得a=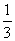 ,b=-
,b=- .
.
∴f(x)= 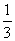 x2-
x2- (x≤0).
(x≤0).
∴f-1(x)=-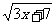 (x≥-
(x≥- ).
).
15.已知函数y=f(x-1)的反函数为y=f-1(x-1),且f(1)=2,则f(2)的值为______________.
答案:1
解析:y=f-1(x-1) x-1=f(y)
x-1=f(y) x=f(y)+1,
x=f(y)+1,
故y=f-1(x-1)的反函数为y=f(x)+1.
故f(x-1)=f(x)+1,即f(x)=f(x-1)-1,
则f(2)=f(1)-1=1.
14.要使函数y=x2-2ax+1在区间[1,2]上存在反函数,则a的取值范围是( )
A.a≤1 B.a≥2 C.a≤1或a≥2 D.1≤a≤2
答案:C
解析:由已知得函数y=x2-2ax+1在区间[1,2]上单调,则a≤1或a≥2.
13.已知f(x)=(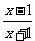 )2(x≥1),
)2(x≥1),
(1)求f(x)的反函数f-1(x),并求出反函数的定义域;
(2)判断并证明f-1(x)的单调性.
解:(1)设y=(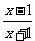 )2
)2 x=
x=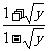 ,又x≥1,
,又x≥1,
∴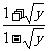 ≥1
≥1 0≤y<1,即f-1(x)=
0≤y<1,即f-1(x)=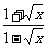 ,f-1(x)的定义域为[0,1].
,f-1(x)的定义域为[0,1].
(2)f-1(x)在[0,1)上单调递增.
证明如下:设0≤x1<x2<1,∴0≤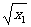 <
<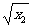 <1.
<1.
∴f-1(x1)-f-1(x2)=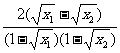 <0.∴f-1(x)在[0,1]上单调递增.
<0.∴f-1(x)在[0,1]上单调递增.
拓展应用 跳一跳,够得着!
12.已知函数f(x)=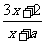 (x≠-a,a≠
(x≠-a,a≠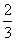 ).
).
(1)求它的反函数;
(2)求使f-1(x)=f(x)的实数a的值;
(3)当a=-1时,求f-1(2).
解:(1)设y=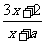 ,∵x≠-a,∴反解得(y-3)x=2-ay.
,∵x≠-a,∴反解得(y-3)x=2-ay.
若y=3,则a=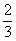 与a≠
与a≠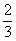 矛盾.
矛盾.
∴y≠3.∴x=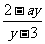 .
.
∴f-1(x)=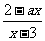 (x≠3,a≠
(x≠3,a≠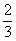 ).
).
(2)当f-1(x)=f(x)时,有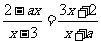 ,
,
整理得(a+3)x2+(a2-9)x-2(a+3)=0.
∴a+3=0,即a=-3.
(3)当a=-1时,由(1)知f-1(x)=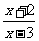 .
.
∴f-1(2)=-4.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com