
题目列表(包括答案和解析)
4.下列函数中,在区间(0,2)上为增函数的是( )
A.y=-x+1
B.y=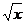
C.y=x2-4x+5
D.y=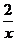
答案:B
解析:C中y=(x-2)2+1在(0,2)上为减函数.
3.若一次函数y=kx+b(k≠0)在(-∞,+∞)上是单调增函数,那么点(k,b)在直角坐标平面的( )
A.上半平面 B.下半平面
C.左半平面 D.右半平面
答案:D
解析:易知k>0,b∈R,∴(k,b)在右半平面.
2.函数f(x)=x2+4ax+2在(-∞,6)内递减,那么实数a的取值范围是( )
A.a≥3 B.a≤3 C.a≥-3 D.a≤-3
答案:D
解析:∵-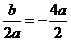 =-2a≥6,∴a≤-3.
=-2a≥6,∴a≤-3.
1.若函数f(x)在区间[m,n]上是增函数,在区间[n,k]上也是增函数,则函数f(x)在区间(m,k)上( )
A.必是减函数 B.是增函数或减函数
C.必是增函数 D.未必是增函数或减函数
答案:C
解析:任取x1、x2∈(m,k),且x1<x2,
若x1、x2∈(m,n],则f(x1)<f(x2),
若x1、x2∈[n,k),则f(x1)<f(x2),
若x1∈(m,n],x2∈(n,k),则x1≤n<x2.
∴f(x1)≤f(n)<f(x2).
∴f(x)在(m,k)上必为增函数.
16.如图,函数的图象由两条射线及抛物线的一部分组成,求函数的解析式.

解:设左侧的射线对应的解析式为y=kx+b(x≤1),由点(1,1)、(0,2)在射线上得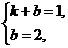 解得k=-1,b=2.
解得k=-1,b=2.
∴左侧射线对应的函数解析式为y=-x+2(x≤1).
同理,右侧射线的解析式为y=x-2(x≥3).
设中间抛物线对应的二次函数解析式为y=a(x-2)2+2(1≤x≤3,a<0),
由点(1,1)在抛物线上可得1=a+2,解得a=-1,则抛物线对应的函数解析式为y=-x2+4x-2(1≤x≤3).
综上,可知函数的解析式可写为
y=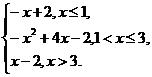
15.从盛满20升纯酒精的容器里倒出1升,然后用水填满,再倒出1升混合溶液后又用水填满,这样继续进行,如果倒第k(k≥1)次时共倒出纯酒精x升,倒第k+1次时共倒出纯酒精f(x)升,则f(x)的函数表达式为( )
A.f(x)=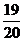 x
B.f(x)=
x
B.f(x)=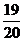 x+1
x+1
C.f(x)=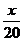 D.f(x)=
D.f(x)=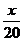 +1
+1
答案:B
解析:f(x)=x+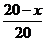 ×1=1+
×1=1+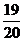 x.
x.
14.已知正方形ABCD的边长为4,动点P从B点开始沿折线BCDA向A点运动.设点P动运的路程为x,△ABP的面积为S,则函数S=f(x)的图象是下图中的( )
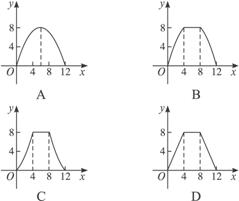
答案:D
解析:f(x)=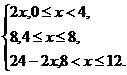 故选D.
故选D.
13.用水清洗一堆蔬菜上残留的农药,对用一定量的水清洗一次的效果作如下假定:用1单位量的水可洗掉蔬菜上残留农药量的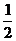 ,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上,设用x单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f(x).
,用水越多洗掉的农药量也越多,但总还有农药残留在蔬菜上,设用x单位量的水清洗一次以后,蔬菜上残留的农药量与本次清洗前残留的农药量之比为函数f(x).
(1)试规定f(0)的值,并解释其实际意义;
(2)试根据假定写出函数f(x)应该满足的条件和具有的性质;
(3)设f(x)=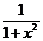 .
.
现有a(a>0)单位量的水,可以清洗一次,也可以把水平均分成2份后清洗两次,试问用哪种方案清洗后蔬菜上残留的农药量比较少?说明理由.
解:(1)f(0)=1表示没有用水洗时,蔬菜上的农药量将保持原样.
(2)函数f(x)应满足的条件和具有的性质是:f(0)=1,f(1)= 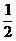 ,在[0,+∞)上f(x)单调递减,且0<f(x)≤1.
,在[0,+∞)上f(x)单调递减,且0<f(x)≤1.
(3)设仅清洗一次,残留的农药量为f1=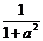 .
.
清洗两次后,残留的农药量为f2=[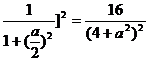 .
.
∴f1-f2=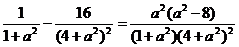 .
.
于是,当a>2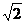 时,f1>f2.
时,f1>f2.
当a=2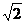 时,f1=f2.
时,f1=f2.
当0<a<2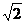 时,f1<f2.
时,f1<f2.
因此,当a>2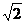 时,清洗两次后残留的农药量较少;当a=2
时,清洗两次后残留的农药量较少;当a=2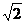 时,两种清洗方法具有相同的效果;当0<a<2
时,两种清洗方法具有相同的效果;当0<a<2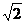 时,一次清洗残留的农药量较少.
时,一次清洗残留的农药量较少.
拓展应用 跳一跳,够得着!
12.已知函数φ(x)=f(x)+g(x),其中f(x)是x的正比例函数,g(x)是x的反比例函数,且φ(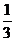 )=16,φ(1)=8,
)=16,φ(1)=8,
(1)求φ(x)的解析式,并指出定义域;
(2)求φ(x)的值域.
解:(1)设f(x)=ax,g(x)=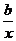 ,a、b为比例常数,
,a、b为比例常数,
则φ(x)=f(x)+g(x)=ax+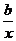 .
.
由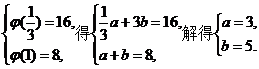
∴φ(x)=3x+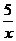 ,
,
其定义域为(-∞,0)∪(0,-∞).
(2)由y=3x+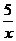 ,得3x2-yx+5=0(x≠0),
,得3x2-yx+5=0(x≠0),
∵x∈R且x≠0,∴Δ=y2-60≥0.
∴y≥2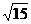 或y≤-2
或y≤-2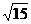 .∴φ(x)的值域为(-∞,-2
.∴φ(x)的值域为(-∞,-2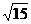 )∪[2
)∪[2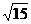 ,+∞).
,+∞).
11.对一切实数x、y,函数f(x)满足f(x·y)=f(x)·f(y)且f(0)≠0,则f(2 006)的值为____________.
答案:1
解析:令x=y=0,则f(0)=f2(0)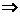 f(0)=1(∵f(0)≠0),再令x=2 006,y=0,则f(0)=f(2
006).f(0)
f(0)=1(∵f(0)≠0),再令x=2 006,y=0,则f(0)=f(2
006).f(0)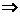 f(2 006)=1.
f(2 006)=1.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com