
题目列表(包括答案和解析)
2.函数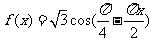 (
(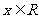 )的最小正周期为 4 .
)的最小正周期为 4 .
1.点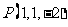 关于
关于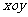 平面的对称点的坐标是 (1,1,2 ) .
平面的对称点的坐标是 (1,1,2 ) .
20.(本小题满分16分)已知圆C过点P(1,1),且与圆M: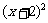 +
+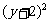 =
=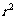 (r>0)关于直线x+y+2=0对称.
(r>0)关于直线x+y+2=0对称.
(1)求圆C的方程;
(2)设Q为圆C上的一个动点,求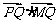 的最小值;
的最小值;
(3)过点P作两条相异直线分别与圆C相交于A,B,且直线PA和直线PB的倾斜角互补,O为坐标原点,试判断直线OP和AB是否平行?请说明理由.
高一年级第二学期热身训练数学试卷
2011-6-18
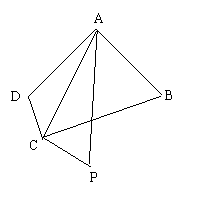
19.(本小题满分16分)如图,在四边形ABCD中,AB=AD=4,BC=6,CD=2,
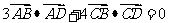
(1) 求四边形ABCD的面积; 源:.Com]
(2) 求三角形ABC的外接圆半径R;
(3) 若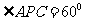 ,求PA+PC的取值范围。
,求PA+PC的取值范围。
18.(本小题满分15分)已知:矩形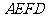 的两条对角线相交于点
的两条对角线相交于点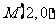 ,
,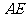 边所在直线的方程为:
边所在直线的方程为: 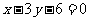 ,点
,点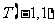 在
在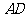 边所在直线上.
边所在直线上.
(1)求矩形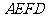 外接圆
外接圆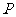 的方程。
的方程。
(2)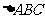 是
是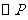 的内接三角形,其重心
的内接三角形,其重心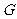 的坐标是
的坐标是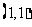 ,求直线
,求直线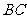 的方程 .
的方程 .
17.(本小题满分15分)已知函数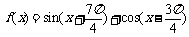 ,x
,x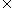 R.
R.
(Ⅰ)求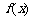 的最小正周期和最小值;
的最小正周期和最小值;
(Ⅱ)已知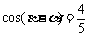 ,
,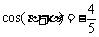 ,
,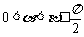 ,求
,求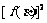 的值.
的值.
16.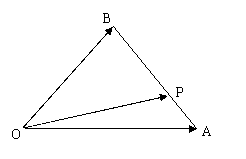 (本小题满分14分)如图,在△ABO中,已知P为线段AB上的一点,
(本小题满分14分)如图,在△ABO中,已知P为线段AB上的一点,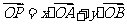 .(1)若
.(1)若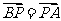 ,求
,求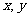 的值;(2)若
的值;(2)若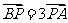 ,
,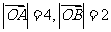 ,且
,且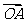 与
与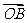 的夹角为
的夹角为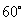 时,求
时,求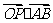 的值.
的值.
15.(本小题满分14分)(1)已知直线l过点P(3,4),它在y轴上的截距是在x轴上截距的2倍,求直线l的方程.
(2)求经过直线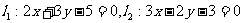 的交点且平行于直线
的交点且平行于直线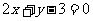 的直线方程
的直线方程
14.O是锐角 ABC所在平面内的一定点,动点P满足:
ABC所在平面内的一定点,动点P满足: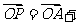
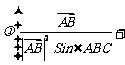
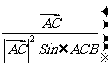 ,
,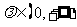 ,则动点P的轨迹一定通过
,则动点P的轨迹一定通过 ABC的 ▲ .
ABC的 ▲ .
13.要测量底部不能到达的电视塔AB的高度,在C点测得塔顶A的仰角是45°,在D点测得塔顶A的仰角是30°,并测得水平面上的∠BCD=120°,CD=40m,则电视塔的高度为 ▲ .
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com