
题目列表(包括答案和解析)
11.函数f(x)=ax2+(a+2)x-1在x∈R上存在反函数,则f-1(1)=_______________.
答案:1
解析:依题意a=0,f(x)=2x-1,令f-1(1)=b,则f(b)=1,即2b-1=1 b=1.
b=1.
10.已知f(x)=3x-2,则f-1[f(x)]=__________________;f[f-1(x)]=__________________.
答案:x x
解析:∵f-1(x)=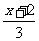 ,
,
∴f-1[f(x)]=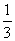 [(3x-2)+2]=x,f[f-1(x)]=3·
[(3x-2)+2]=x,f[f-1(x)]=3·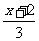 -2=x.
-2=x.
一般地,f[f-1(x)]与f-1[f(x)]的表达式总为x,但两个函数定义域不一定相同,故不一定是同一个函数.
9.函数f(x)是增函数,它的反函数是f-1(x),若a=f(2)+f-1(2),b=f(3)+f-1(3),则下面结论中正确的是( )
A.a<b B.a=b C.a>b D.无法确定
答案:A
解析:∵f(x)是增函数,故其反函数f-1(x)也是增函数,∴f(3)>f(2),f-1(3)>f-1(2),即b>a.
8.函数y=2|x|在下面的区间上,不存在反函数的是( )
A.[0,+∞]) B.(-∞,0)] C.[-4,4] D.[2,4]
答案:C
解法一:函数若在区间上单调,则存在反函数,易知函数y=2|x|在[0,+∞),(-∞,0],[2,4]上单调.
解法二:当x=±4时,y=8,知不是一一映射.
7.求下列函数的反函数:
(1)y=-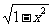 (-1≤x<0);
(-1≤x<0);
(2)y=-x2-2x+1(1≤x≤2);
(3)y=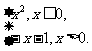
解:(1)由y=-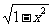 ,得y2=1-x2,
,得y2=1-x2,
即x2=1-y2.
∵-1≤x<0,
∴x=-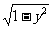 .
.
又∵y=-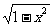 ,-1≤x<0,
,-1≤x<0,
∴-1<y≤0.
∴所求反函数为y=-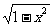 (-1<x≤0).
(-1<x≤0).
(2)由y=-x2-2x+1=-(x+1)2+2,得(x+1)2=2-y.
∵1≤x≤2,
∴2≤x+1≤3.
∴x+1=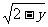 ,即x=-1+
,即x=-1+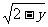 .
.
∴反函数为y=-1+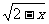 (-7≤x≤-2).
(-7≤x≤-2).
(3)①由y=x2(x≤0),得x=-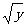 ,即y=x2(x≤0)的反函数为y=-
,即y=x2(x≤0)的反函数为y=-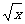 (x≥0).
(x≥0).
②由y=-x-1(x>0),得x=-y-1,即y=-x-1(x>0)的反函数为y=-x-1(x<-1).
由①②可知f(x)=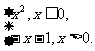 的反函数为f-1(x)=
的反函数为f-1(x)=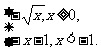
能力提升 踮起脚,抓得住!
6.已知f(x)=x2-1(x≥2),则f-1(4)=______________.
答案: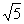
解析:因为f(x)=x2-1,x≥2,所以其反函数为f-1(x)=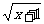 (x≥3).
(x≥3).
所以f-1(4)=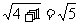 .
.
5.设y=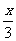 +m和y=nx-9互为反函数,那么m、n的值分别是( )
+m和y=nx-9互为反函数,那么m、n的值分别是( )
A.-6,3 B.2,1 C.2,3 D.3,3
答案:D
解析:求出y=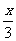 +m的反函数y=3x-3m,再与y=nx-9对比系数即得.
+m的反函数y=3x-3m,再与y=nx-9对比系数即得.
4.若函数y=f(x)的反函数是y=-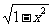 (-1≤x≤0),则原函数的定义域是( )
(-1≤x≤0),则原函数的定义域是( )
A.(-1,0) B.[-1,1] C.[-1,0] D.[0,1]
答案:C
解析:∵原函数的定义域为反函数的值域,
又-1≤x≤0,
∴0≤1-x2≤1,即y∈[-1,0].
3.若函数f(x)的反函数f-1(x)=1+x2(x<0),则f(2)等于( )
A.1 B.-1 C.1和-1 D.5
答案:B
解法一:由y=1+x2(x<0),得x=-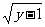 .故f(x)=-
.故f(x)=-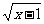 (x>0),f(2)=-
(x>0),f(2)=-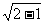 =-1.
=-1.
解法二:令1+x2=2(x<0),则x=-1,即f(2)=-1.
2.函数y=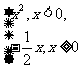 的反函数是( )
的反函数是( )
A.y=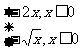 B.y=
B.y=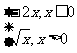
C.y=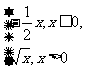 D.y=
D.y=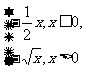
答案:A
解析:当x<0时,由y=x2,得x=-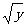 .故反函数为y=f-1(x)=-
.故反函数为y=f-1(x)=-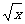 (x>0).
(x>0).
当x≥0时,由y=-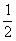 x,得x=-2y.
x,得x=-2y.
故反函数为y=f-1(x)=-2x(x≤0).
∴y=f-1(x)=-x,x>0,
-2x,x≤0.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com