
题目列表(包括答案和解析)
4.设函数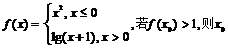 的取值范围为( )
的取值范围为( )
A.(-1,1) B.(-1,+∞) C.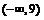 D.
D.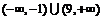
3.函数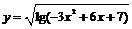 的值域是( )
的值域是( )
A.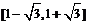 B.[0,1]
C.[0,
B.[0,1]
C.[0,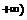 D.{0}
D.{0}
2.设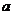 表示
表示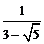 的小数部分,则
的小数部分,则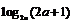 的值是( )
的值是( )
A.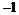 B.
B.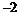 C.0 D.
C.0 D.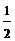
1.若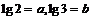 ,则
,则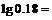 ( )
( )
A.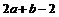 B.
B.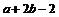 C.
C.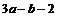 D.
D.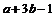
22.(本小题满分14分)
已知点(1,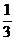 )是函数
)是函数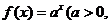 且
且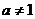 )的图象上一点,等比数列
)的图象上一点,等比数列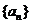 的前
的前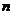 项和为
项和为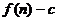 ,正项数列
,正项数列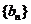 的首项为
的首项为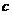 ,且
,且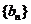 的前
的前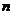 项和
项和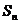 满足:
满足:
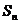 -
-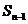 =
=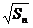 +
+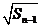 (
(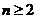 ).
).
(Ⅰ)求数列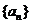 的通项公式;
的通项公式;
(Ⅱ)求数列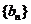 的通项公式;
的通项公式;
(Ⅲ)若数列{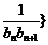 前
前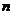 项和为
项和为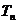 ,求使
,求使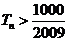 恒成立的最小正整数
恒成立的最小正整数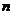 。
。
21.(小题满分12分)
围建一个面积为360m2的矩形场地,要求矩形场地的一面利用旧墙(利用旧墙需维修)其它三面围墙要新建,在旧墙的对面的新墙上要留一个宽度为2m的进出口,如图所示,已知旧墙的维修费用为45元/m,新墙的造价为180元/m,设利用的旧墙的长度为x (单位:m),此矩形场地围墙的总费用为y(单位:元).
(Ⅰ)将y表示为x的函数:
(Ⅱ)试确定x,使修建此矩形场地围墙的总费用最小,并求出最小总费用.

20.(小题满分12分)
已知函数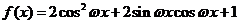 (
(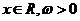 )的最小正周期是
)的最小正周期是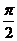 .
.
(Ⅰ)求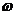 的值;
的值;
(Ⅱ)求函数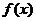 的单调递减区间;
的单调递减区间;
(Ⅲ)若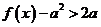 在
在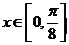 上恒成立,求实数a的取值范围.
上恒成立,求实数a的取值范围.
19.(本小题满分12分)
棱锥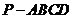 的底面是正方形,
的底面是正方形,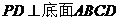 ,点E在棱PB上.
,点E在棱PB上.
(Ⅰ)求证:平面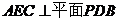 ;
;
 (Ⅱ)当
(Ⅱ)当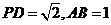 ,且E为PB的中点时,求1AE与平面PDB所成的角的大小;2求异面直线AE和CD所成角的大小.
,且E为PB的中点时,求1AE与平面PDB所成的角的大小;2求异面直线AE和CD所成角的大小.
18.(本小题满分12分)
设锐角三角形ABC的内角A,B,C的对边分别为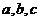 ,
,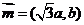 ,
,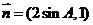 ,且
,且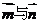 共线。
共线。
(Ⅰ)求B的大小;
(Ⅱ)若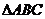 的面积是
的面积是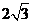 ,
,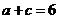 ,求
,求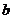 .
.
17. (本小题满分12分)
(Ⅰ)求过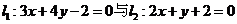 的交点,且平行于直线
的交点,且平行于直线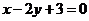 的
的
直线的方程;
(Ⅱ)求垂直于直线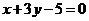 , 且与点
, 且与点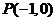 的距离是
的距离是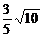 的直线的方程.
的直线的方程.
湖北省互联网违法和不良信息举报平台 | 网上有害信息举报专区 | 电信诈骗举报专区 | 涉历史虚无主义有害信息举报专区 | 涉企侵权举报专区
违法和不良信息举报电话:027-86699610 举报邮箱:58377363@163.com